数学人教版5.3.2 命题、定理、证明教课内容ppt课件

这是一份数学人教版5.3.2 命题、定理、证明教课内容ppt课件，共30页。PPT课件主要包含了下列语句是命题吗，什么是命题，题设是，结论是，两个角是邻补角，这两个角互补，a＞bb＞c，④同位角相等，两个角是对顶角，这两个角相等等内容，欢迎下载使用。

下列语句在表述形式上，哪些是对事情作了判断？哪些没有对事情作出判断？1、对顶角相等；2、画一个角等于已知角；3、两直线平行，同位角相等；4、a、b两条直线平行吗？5、温柔的李明明；6、玫瑰花是动物；7、若a2＝4，求a的值；8、若a2＝b2，则a＝b。
对事情作了判断的语句是否正确？
（2）、如果一个句子没有对某一件事情作出任何判断，那么它就不是命题。
如：画线段AB=CD。
1.定义：判断一件事情的语句叫做命题。
注意：（1）、只要对一件事情作出了判断，不管正确与否，都是命题。
如：相等的角是对顶角。
句子 ① ② ③ 能判断一件事情. 是命题
句子 ④ ⑤ ⑥ 不能判断一件事情. 不是命题
问题2 　判断下列语句是不是命题？（1）你饭吃了吗？（ ）（2）两点之间，线段最短。（ ）（3）请画出两条互相平行的直线。 （ ）（4）过直线外一点作已知直线的垂线。 （ ）（5）如果两个角的和是90º，那么这两个角互余。（ ）（6）对顶角不相等。（ ）
判断一件事情的语句，叫做命题.
你能举一些不是命题的例子吗？
问题4　请同学们观察一组命题，并思考命题是由几部分组成的？（1）如果两条直线都与第三条直线平行， 那么这两条直线也互相平行；（2）两条平行线被第三条直线所截， 同旁内角互补；（3）如果两个角的和是90º， 那么这两个角互余；（4）等式两边都加同一个数， 结果仍是等式．（5）两点之间，线段最短．
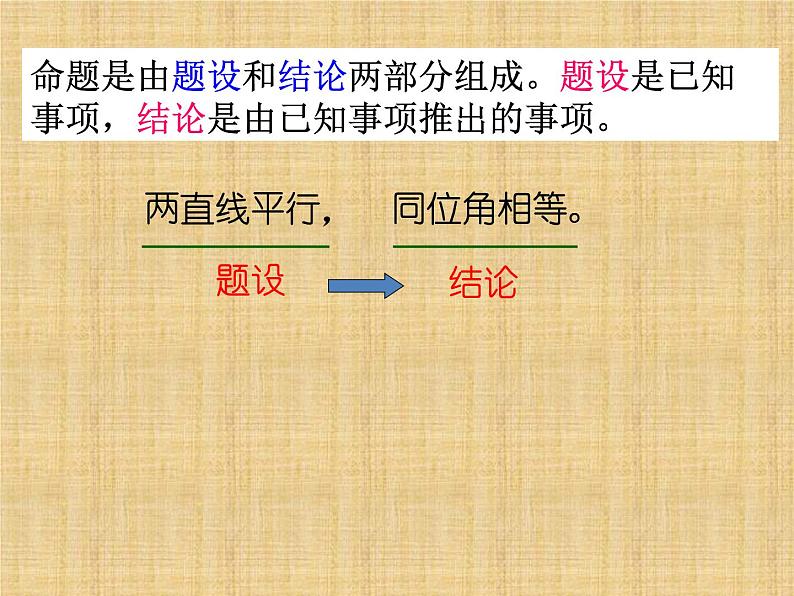
命题是由题设和结论两部分组成。题设是已知事项，结论是由已知事项推出的事项。
两直线平行， 同位角相等。
3.命题一般都写成“如果…，那么…”的形式。“如果”后接的部分是题设，“那么”后接的部分是结论。
如命题：熊猫没有翅膀。改写为：
如果这个动物是熊猫，那么它就没有翅膀。
注意：添加“如果”、“那么”后，命题的意义不能改变，改写的句子要完整，语句要通顺，使命题的题设和结论更明朗，易于分辨，改写过程中，要适当增加词语，切不可生搬硬套。
下列命题中的题设是什么？结论是什么？
② 如果a＞b，b＞c，那么a=c .
①如果两个角是邻补角，那么这两个角互补
如果两个角是对顶角，那么这两个角相等.
如果两个角是同位角，那么这两个角相等.
例2：把下列命题写成“如果……那么……”的形式。并指出它的题设和结论。
1、对顶角相等；2、内错角相等；3、两直线被第三直线所截，同位角相等；4、同平行于一直线的两直线平行；5、 直角三角形的两个锐角互余；6、等角的补角相等；7、正数与负数的和为0。
有些命题如果题设成立，那么结论一定成立；而有些命题题设成立时，结论不一定成立。
如命题：“如果两个角互补，那么它们是邻补角”就是一个错误的命题。
如命题：“如果一个数能被4整除，那么它也能被2整除”就是一个正确的命题。
问题中哪些命题是正确的，哪些命题是错误的？（1）两条直线被第三条直线所截，同旁内角互补；（2）等式两边都加同一个数，结果仍是等式；（3）互为相反数的两个数相加得0；（4）同旁内角互补；（5）对顶角相等．
问题　请同学们举例说出一些真命题和假命题．
真命题：如果题设成立，那么结论一定成立， 这样的命题叫做真命题．
假命题：如果题设成立时，不能保证结论一定成立， 这样的命题叫做假命题．
2）两条直线相交，有且只有一个交点（ ）
4）一个平角的度数是180度（ ）
6）取线段AB的中点C；（ ）
1）长度相等的两条线段是相等的线段吗？（ ）
7）画两条相等的线段（ ）
练习1：下列语句是不是命题？是用“√”，不是用“× 表示。
3）不相等的两个角不是对顶角（ ）
5）相等的两个角是对顶角（ ）
5）若A=B，则2A = 2B（ ）
9）同旁内角互补（ ）
4）两点可以确定一条直线（ ）
1）互为邻补角的两个角的平分线互相垂直（ ）
2）一个角的补角大于这个角（ ）
2：判断下列命题的真假。真的用“√”， 假的用“× 表示。
7）两点之间线段最短（ ）
3）相等的两个角是对顶角（ ）
8）同角的余角相等（ ）
6）锐角和钝角互为补角（ ）
3.下列句子哪些是命题？是命题的，指出是真命题还是假命题？
1、猪有四只脚； 2、内错角相等； 3、画一条直线； 4、四边形是正方形； 5、你的作业做完了吗？ 6、同位角相等，两直线平行； 7、对顶角相等； 8、同垂直于一直线的两直线平行； 9、过点P画线段MN的垂线；10、x＞2
命题1　在同一平面内，如果一条直线垂直于两条平行线中的一条，那么它也垂直于另一条．
（3）这个命题的题设和结论分别是什么呢？
在同一平面内，一条直线垂直于两条平行线中的一条；
这条直线也垂直于两条平行线中的另一条．
（4）你能结合图形用符号语言表述命题的题设和结论吗？
命题1　 在同一平面内，如果一条直线垂直于两条平行线中的一条，那么它也垂直于另一条.
已知：b∥c， a⊥b ．
（5）请同学们思考如何利用已经学过的定义定理来证明这个结论呢？
已知：b∥c，a⊥b ．
证明：∵ a⊥b（已知），
又∵ b∥c（已知），
∴∠1=∠2（两直线平行，同位角相等）.
∴∠2=∠1=90º（等量代换）．
∴∠1=90º （垂直的定义）．
∴ a⊥c（垂直的定义）．
问题　请同学们判断下列两个命题的真假，并思考如何判断命题的真假．
命题2 相等的角是对顶角．
（1）判断这个命题的真假．
（2）这个命题题设和结论分别是什么？
结论：这两个角互为对顶角．
（3）你能举出反例吗？
问题3　请同学们判断下列两个命题的真假，并思考如何判断命题的真假．
命题2 相等的角是对顶角．
5、数学中有些命题的正确性是人们在长期实践中总结出来的，并把它们作为判断其他命题真假的原始依据，这样的真命题叫做公理。
6、有些命题可以从公理或其他真命题出发，用逻辑推理的方法判断它们是正确的，并且可以进一步作为判断其他命题真假的依据，这样的真命题叫做定理。
公理和定理都可作为判断其他命题真假的依据。
有些命题的正确性是人们在长期实践中总结出来的，这样的真命题叫做公理。
有些命题的正确性是经过推理证实的，这样的真命题叫做定理。
经过两点有且只有一条直线。
连接两点的所有连线中，线段最短。
经过直线外一点，有且只有一条直线与已知直线平行。
如:平行线判定定理； 平行线性质定理； 同角的补角相等。
两点的所有连线中，线段最短。
同位角相等，两直线平行。
两直线平行，同位角相等。
同角或等角的补角相等。
同角或等角的余角相等。
①过一点有且只有一条直线与已知直线垂直；
如果两条直线都和第三条直线平行，那么这两条直线也互相平行。
内错角相等，两直线平行。
同旁内角互补，两直线平行。
6、平行线的判定定理：
7、平行线的性质定理：
两直线平行，内错角相等。
两直线平行，同旁内角互补。
1、命题：判断一件事情的语句叫命题。
2、公理：人们在长期实践中总结出来的真命题叫做公理。
3、定理：经过推理证实的真命题叫做定理。
4、判断一个命题是真命题，可以从公理或定理出发，用逻辑推理的方法证明（公理和定理都是真命题）； 判断一个命题是假命题，只要举出一个例子，说明该命题不成立就可以了，这种方法称为举反例。
（1）命题的结构：命题由题设和结论两部分构成，常可写成“如果…，那么…”的形式。（2）命题的分类：正确的命题称为真命题，错误的命题称为假命题。