人教版七年级下册6.1 平方根教课内容ppt课件

这是一份人教版七年级下册6.1 平方根教课内容ppt课件，共20页。PPT课件主要包含了的算术平方根是0，负数没有算术平方根，或x-3，－32＝9，平方根定义，负数没有平方根，平方根的性质，正数a的算术平方根，正数a的平方根，平方根的表示方法等内容，欢迎下载使用。

1．强化对平方根与算术平方根的理解，理解它们之间的关系2. 能熟练地求一些实数的平方根与算术平方根.3．理解平方根的性质，并能灵活运用
(1)什么是算术平方根?怎样表示?
如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.
a的算术平方根表示为:
(2)256的算术平方根是 ，5的算术平方根是 .
(3)下列各式有意义的条件是什么？
(4) ①一块正方形菜地的边长是3米，这块菜地的面积是多少平方米？②已知一块正方形菜地的面积是9平方米，求它的边长.③如果一个数的平方等于9，这个数是多少？
如果一个数的平方等于9，那么这个数是多少？
∴平方等于9的数是3或－3.
3或－3可以简单记作：±3.
一般地，如果一个数的平方等于a，那么这个数叫做a的平方根或二次方根，这就是说，如果x2=a，那么x叫做a的平方根.
例如:3和-3是9的平方根,简记为±3是9的平方根.
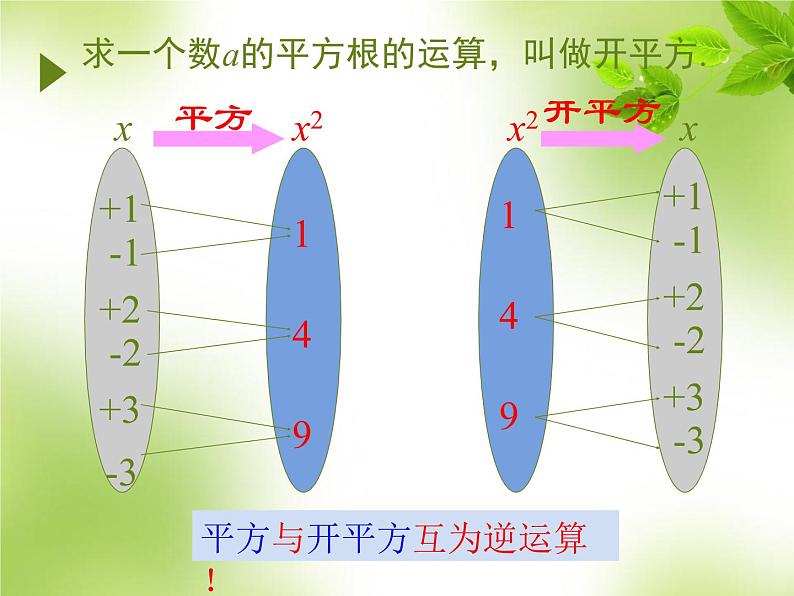
求一个数a的平方根的运算，叫做开平方.
平方与开平方互为逆运算！
解：(1) ∵(±10)2＝100， ∴100的平方根是±10；
(3) ∵(±0.5)2＝0.25， ∴0.25的平方根是±0.5.
1.一个正数有几个平方根？ 它们有什么特点？2.0有几个平方根？是多少？3.负数呢？
1.正数的平方根有两个，它们互为相反数.
2.0有一个平方根，它是0本身.
正数有2个平方根，它们互为相反数；0的平方根是0；负数没有平方根.
读作 “正、负根号a”
25的平方根是±5,用符号语言表达为:
正数a的算术平方根的相反数（即正数a的负的平方根）
例如：9的平方根是±3,用符号语言表达为:
解：(1) ∵(±10)2＝100，
(3) ∵(±0.5)2＝0.25，
(2) ∵(± )2＝ ，
∴100的平方根是±10；
∴0.25的平方根是±0.5.
1.平方根包括算术平方根，算术平方根是平方根中非负的那一个.2.存在条件相同.只有非负数才有平方根和算术平方根.3.0的平方根和算术平方根均为0
正数a的算术平方根有一个
如果一个正数x的平方等于a，那么这个正数就叫做a的算术平方根
如果一个数的平方等于a，这个数就叫做a的平方根
平方根与算术平方根的比较
例5. 求下列各式的值.
4.计算下列各式的值：
3.如果一个正数的平方根是a-1和a+3,则a=____，
本节课你学习了哪些知识？在探索知识的过程中，你用了哪些方法？对你今后的学习有什么帮助？
知识方面：平方根的概念、表示方法、求法及平方根的性质.思维方法：平方运算和开平方运算互为逆运算，可以互相检验.探究策略：由特殊到一般，再由一般到特殊，是发现问题和解决问题的基本方法和途径.用定义解决问题也是常用的方法.
解下列方程：（1）4x2=9；（2）x2-81=0；（3）（x+1）2=1.