数学人教版7.1.2平面直角坐标系背景图ppt课件

这是一份数学人教版7.1.2平面直角坐标系背景图ppt课件，共53页。PPT课件主要包含了回顾与思考，探究1，点到两轴的距离，巩固练习，探究2，探究3，a－b，想一想，探究4，基础训练等内容，欢迎下载使用。

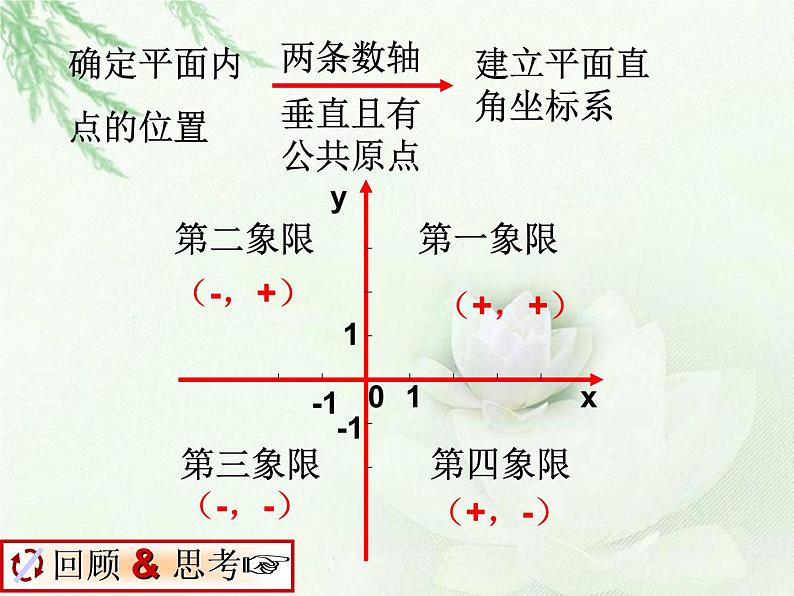
1、什么是平面直角坐标系？2、两条坐标轴如何称呼，方向如何确定？3、坐标轴分平面为四个部分，分别叫做什么？4、什么是点的坐标？平面内点的坐标有几部分组成？5、各个象限内的点的坐标有何特点？ 坐标轴上的点的坐标有何特点？6、坐标轴上的点属于什么象限？
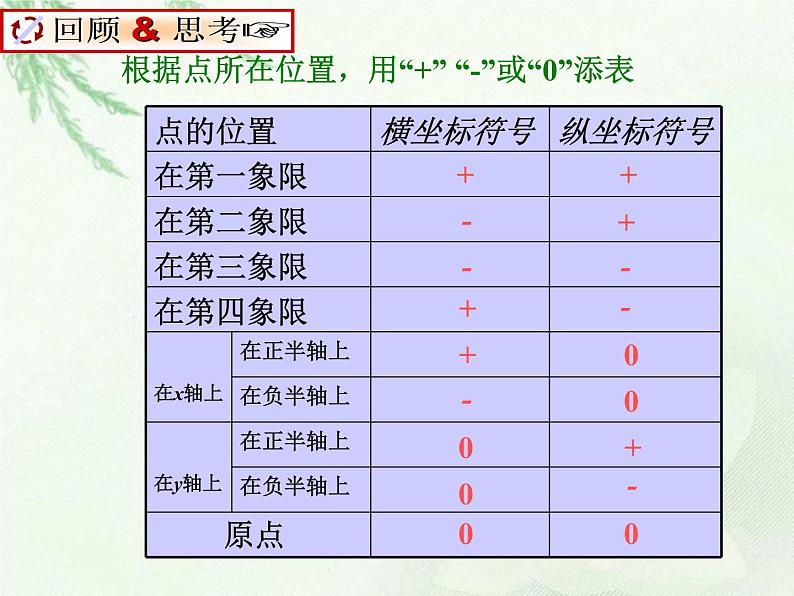
根据点所在位置，用“+” “-”或“0”添表
.设点M（a，b）为平面直角坐标系中的点当a>0，b<0时点M位于第几象限？当ab>0时，点M位于第几象限？当a为任意数时，且b<0时，点M直角坐标系中的位置是什么？
正方形ABCD的边长为6, 如果以点A为原点，AB所在直线为X轴，建立平面直角坐标系，那么y轴是哪条线? 写出正方形的顶点A、B、C、D的坐标。
请另建立一个平面直角坐标系，这时正方形的顶点A、B、C、D的坐标又分别是多少?与同学交流一下。
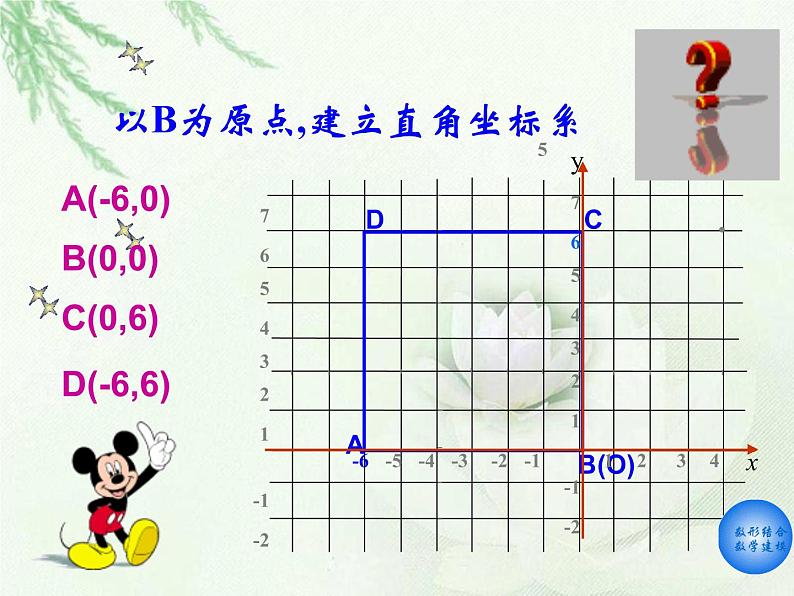
A(0,0),B(6,0),C(6,6),D(0,6)
以B为原点,建立直角坐标系
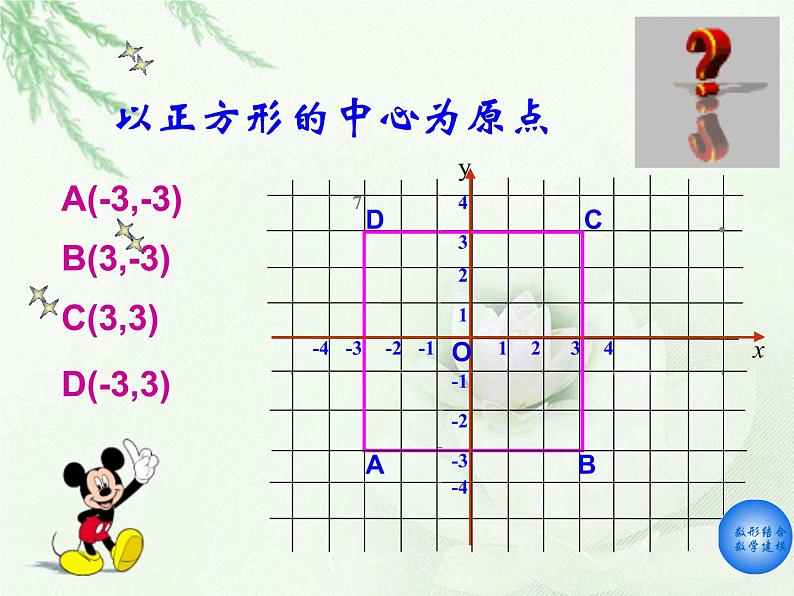
以图中的O点为坐标原点呢?
结论:对同一图形,坐标原点取的不同,相应点的坐标不同。
你知道A、B两点到X轴和y轴的距离是多少吗？
例：点A（2,3）到x轴的距离是 ，到y轴的距离是
点B（-5,4）到x轴的距离是 ，到y轴的距离是
点C（-2,-3）到x轴的距离是 ，到y轴的距离是
点D（2,3）到x轴的距离是 ，到y轴的距离是
.已知点P（3，a），并且P点到x轴的距离是2个单位长度，求P点的坐标。
分析：由一个点到x轴的距离是该点纵坐标的绝对值，所以a的绝对值等于2，这样a的值应等于±2。
解：因为P到X轴的距离是2 ，所以，a的值可以等于±2，因此P（3，2）或P（3，-2）。
1、已知点M（2，-3），则M到x轴的距离为　　　，到ｙ轴的距离为 。
2、已知点P到x轴和y轴的距离分别是2和5，求P点的坐标。
P(5,2) 或P(5,-2) 或P(-5,2)或P(-5,-2)
点Ｐ（x,y)到x轴的距离为∣y∣,到y轴的距离为∣x∣.例如，点A（－3，4）到x轴的距离为４，到y轴的距离为３．
注意：点Ｐ（x,y)到两轴的距离是一个非负数．例如点A（－3，4）到y轴的距离为３而不是－３
2.点A在x轴上，距离原点4个单位长度，则A点的坐标是 _______________。
3.若点P在第三象限且到x轴的距离为 2 ，到y轴的距离为1.5，则点P的坐标是 。
1.点 M（- 8，12）到 x轴的距离是_________， 到 y轴的距离是________.
(4,0)或(-4,0)
4．点Ｐ到x轴、y轴的距离分别是２、１，则点Ｐ的坐标可能为 。　　
(1,2)、(1,-2)、(-1,2)、(-1,-2)
6.若点（a,b-1)在第二象限，则a的取值范围是_____，b的取值范围______。
7.实数x，y满足(x-1)2+|y|=0，则点P（x，y）在（ ）. （A）原点（B）x轴正半轴（C）第一象限（D）任意位置
5.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在____________。
8、如果点P（m+3,m+1)在平面直角坐标系的y轴上，那么点P的坐标是 。
如图，分别写出八边形各个顶点的坐标。
上面问题中点Ｂ和Ｃ的坐标之间有什么关系？B、C的边线与坐标轴有什么关系？D、E呢？
　　线段ＡＫ、EＧ与Ｘ轴有什么位置关系？点Ａ点Ｋ的纵坐标有什么特点？点E点Ｇ呢？
　　线段ＢＤ、ＧＪ与Ｘ轴有什么位置关系？点Ｂ点Ｄ的横坐标有什么特点？ 点Ｇ点J呢？
与坐标轴平行的直线上的点的特点
平行于x轴直线上的点纵坐标相同
平行于y轴直线上的点横坐标相同
纵坐标相同的点的连线平行于x轴
横坐标相同的点的连线平行于y轴
A与D、B与C的纵坐标相同吗？为什么？A与B，C与D的横坐标相同吗？为什么？
写出平行四边形ABCD各个顶点的坐标。
描出下列各点A(5,5) B(3,3) C(2，2) D(-2，-2) E(-4，-4)
大家发现这些点有什么特点？
横纵坐标相同的点在一三象限的角平分线上
描出下列各点A(-4,4) B(-2,2) C(4，-4) D( 3，-3)
横纵坐标互为相反数的点在二四象限的角平分线上
小结： 当点P （a，b）落在一、三象限的两条坐标轴夹角平分线上时。点P （a，b）具有什么特征？
小结： 当点P （a，b）落在二、四象限的两条坐标轴夹角平分线上时。点P （a，b）具有什么特征？
x,y轴夹角平分线上的点的坐标特征
y = x 或y-x=0
y = - x或y+x=0
分别写出图中点A、B、C、D的坐标。观察图形，并回答问题
点A与点B的位置有什么特点?点A与点B的坐标有什么关系?
点A与点C的位置有什么特点?点A与点C的坐标有什么关系?
点B与点C的位置有什么特点?点B与点C的坐标有什么关系?
关于x轴对称的点的横坐标相同,纵坐标互为相反数
关于y轴对称的点的纵坐标相同,横坐标互为相反数
关于原点对称的点的横坐标、纵坐标都互为相反数
点A与点D关于X轴对称
横坐标相同,纵坐标互为相反数
点A与点B关于Y轴对称
纵坐标相同,横坐标互为相反数
点A与点C关于原点对称
横坐标、纵坐标 均互为相反数
平面直角坐标系中对称点的坐标特征
若设点P（a,b),则 P点关于X轴的对称点P1（ ） P点关于Y轴的对称点P2（ ） P点关于原点O的对称点P3（ ）
C（-3,- 2 ）
你能说出点P关于x轴、y轴、原点的对称点坐标吗？
1、若设点M（a,b), M点关于X轴的对称点M1（ ） M点关于Y轴的对称点M2（ ）， M点关于原点O的对称点M3（ ）
2、点A（1-a，5），B（3 ,b）关于y轴对称，则a=___,b=____
1、点（-1，2）与点（ 1，-2）关于 对称， 点（-1，2）与点（-1，-2）关于 对称， 点（1，-2）与点（-1，-2）关于 对称。
3、若点A（a-1,a）在第二象限，则点B（a，1-a）在第 象限。
（1）关于x轴对称的两点，横坐标相等，纵坐标互为相反数．如A（3，-3）和 B（3，3）
（２）关于y轴对称的两点，纵坐标相等，横坐标互为相反数．如C（-3，3）和 B（3，3）
　（３）关于原点对称的两点，横纵坐标分别互为相反数．如C（-3，3）和A（3，- 3） B（3，3）和 D（-3，-3）　　
练习(1)若点P(m,n)在第二象限，则点Q（－m,-n)在第（　　　）象限（２）如果点Ａ（a²+1,-1-b²),那么点Ａ在第几象限．（３）点Ｍ（３，－４）关于x轴的对称点M′的坐标是（　　）　　A (3,4) B (-3,-4) C (-3,4) D (-4,3) (4)点Ａ（m-4,1-2m)在第三象限，则m的取值范围是（　　）Ａ　m﹥1／２ B m﹤4 C 1／2 ﹥m﹤4 D m﹥4 　　　
(5)坐标平面内点Ｐ（m,2)与点Ｑ（３，－２）关于原点对称，则m＝　　　　　　　　　　　　　　　　　　　　　（６）已知，点Ａ（3a+5,-6a-2)在第二四象限的角平分线上，求a2005-a的值（７）若点Ｐ（x,y)满足xy﹥０，则点p在第几象限？（８）当2\3 ﹤ m ﹤1时，点P（３m-2,m-1)在（　）Ａ第一象限Ｂ第二象限Ｃ第三象限Ｄ第四象限（９）如果∣3x+2∣+∣2y-1∣=0,那么点Ｐ（x,y)和Ｑ（x+1,y-2)分别在哪个象限？
例1 已知A(-2,0)，B（4，0），C（x,y) (1)若点C在第二象限，且|x|=4,|y|=4求点C的坐标，并求三角形ABC的面积； （2）若点C在第四象限上，且三角形ABC的面积=9，|x|=3,求点C的坐标
分析(1)由点C在第二象限，可知x和y的符号，这样可化简绝对值，从而求点C的坐标，求三角形的面积，关键求点C到AB所在的直线即x轴的距离|y|
例1 已知A(-2,0)，B（4，0），C（x,y) (1)若点C在第二象限，且|x|=4,|y|=4求点C的坐标，并求三角形ABC的面积；
解：如图：∵点C在第二象限
例1 已知A(-2,0)，B（4，0），C（x,y) （2）若点C在第四象限上，且三角形ABC的面积=9，|x|=3,求点C的坐标
分析：由三角形的面积可求出C到AB所在的直线距离为3,而点C在第四象限可知它的坐标符号，从而可知y=-3
解：如图：∵三角形ABC的面积=
1.平面直角坐标系中的点p（x，y）到x轴的距离是|y| ；到y轴的距离是 |x|；2.平面直角坐标系中的点p（x，y）关于x轴的对称点是（x，-y）；关于y轴的对称点是（-x，y）；关于原点的对称点是p（-x，-y）。
练习： 1.在y轴上的点的横坐标是（ ），在x轴上的点的纵坐标是（ ）. 2.点 A（2，- 3）关 于 x 轴 对 称 的 点 的 坐 标 是（ ）. 3.点 B（ - 2，1）关 于 y 轴 对 称 的 点 的 坐 标 是（ ）.
4.点 M（- 8，12）到 x轴的距离是（ ），到 y轴的距离是（ ） . 5.点（4，3）与点（4，- 3）的关系是（ ） . （A）关于原点对称 （B）关于 x轴对称 （C）关于 y轴对称 （D）不能构成对称关系
4.点A（1-a，5），B（3 ,b）关于y轴对称， 则a=___,b=___。
5.实数 x，y满足 (x-1)2+|y|=0，则点P(x，y)在( ). （A）原点 （B）x轴正半轴（C）第一象限 （D）任意位置
4 . 直角坐标系内点P（－２，３）关于原点的对称点Q的坐标为（ ）A．（2，－３） B．（２，３） C．（－２，３） D．（－２，－３）
2. 点P（a，3）、Q(－2，b)关于X轴对称，则a＝________，b＝_______．
3．在平面直角坐标系中，点A(2,5)与点B关于y轴对称，则点B的坐标是（ ）A.(-5,-2)B.(-2,-5) C.(-2,5) D.(2，-5)
1．点P(3,-5)关于x轴对称的点的坐标为（　　）A.(-3,-5) B.(5,3) C.(-3,5) D.(3,5)
5、平面内点的坐标是（ ） A、一个点 B、一个图形 C、一个实数 D、一对有序实数
6、在平面直角坐标系内，下列说法错误的是（ ） A、原点O不在任何象限内 B、原点O的坐标是0 C、原点O既在X轴上也在Y轴上 D、原点O在坐标平面内
7.过点B（-3，-1）作x轴的垂线，垂足对应的数是——，过点B作y 轴的垂线，垂足对应的数是——。8.点A(3, a )在x 轴上，点B（b,4)在y轴上，则a=——，b=——
9.如图１所示,点A的坐标是 ( ) A.(3,2); B.(3,3); C.(3,-3); D.(-3,-3)10.如图１所示,横坐标和纵坐标都是负数的点是 ( ) A.A点 B.B点 C.C点 D.D点11.如图１所示,坐标是(-2,2)的点是 ( ) A.点A B.点B C.点C D.点D12. 在平面直角坐标系内，下列各点在第四象限的是( )　A.(2,1) 　B.(-2,1) 　 C.(-3,-5) 　 D.(3,-5)
13.若点M的坐标是(a,b),且a>0,b<0,则点M在( 　 ) 　A.第一象限　　　　 B.第二象限　C.第三象限　　　　　D.第四象限14．若点P(a,b) 在第一象限内，则a,b的取值范围是（　　） A.a>0,b<0 B.a>0,b>0 C.a<0,b>0 D.a<0,b<0
象限中点的坐标符号的情况及坐标轴上点的坐标特点
平面内特殊位置点的坐标：x,y轴夹角平分线上的点的坐标特征平行于坐标轴的点的坐标特征关于X轴，Y轴及原点对称的坐标的特征
特殊位置的点的坐标特点： ⑴ x轴上的点，纵坐标为0。 y轴上的点，横坐标为0。 ⑵ 第一、三象限夹角平分线上的点，纵横坐标相等。 第二、四象限夹角平分线上的点，纵横坐标互为相反数。 ⑶与x轴平行（或与y轴垂直）的直线上的点纵坐标都相同。 与y轴平行（或与x轴垂直）的直线上的点横坐标都相同。 ⑷关于x轴对称的点横坐标相同、纵坐标互为相反数。 关于y轴对称的点纵坐标相同、横坐标互为相反数。 关于原点对称的点纵横坐标都互为相反数。 ⑸平面直角坐标系中有一点P(a , b)，点P到x轴的距离是这个点的 纵坐标的绝对值；点P到y轴的距离是这个点的横坐标的绝对值；
注意：上述所有规律，正着说对，反着说也对。
同学们，其实我们每个人的人生就是一个以时间为横轴，以人的价值为纵轴的平面直角坐标系，我相信同学们一定能用自己的勤奋和智慧在这个坐标系中画出一个个光彩夺目的点，构画出辉煌的人生。