华师大版八年级上册1 两数和乘以这两数的差教课ppt课件

这是一份华师大版八年级上册1 两数和乘以这两数的差教课ppt课件，共18页。PPT课件主要包含了导入新课，讲授新课，a+5a-5，面积变了吗，x2－12，m2－22，2m2－12，5y2－z2，a2−b2，公式变形等内容，欢迎下载使用。

1.理解两数和乘以这两数差的几何意义.（重点）2.理解并掌握两数和乘以这两数差的公式结构，并能正确运算.（难点）
王剑同学去商店买了单价是9.8元／千克的糖块10.2千克，售货员刚拿起计算器，王剑就说出应付99.96元，结果与售货员计算出的结果相吻合.售货员惊讶地问：“这位同学，你怎么算得这么快?”王剑同学说：“我利用了在数学上刚学过的一个公式.”你知道王剑同学用的是一个什么样的公式吗?你现在能算出来吗?学了本节之后，你就能解决这个问题了.
①(x ＋ 1)( x－1)；②(m ＋ 2)( m－2)； ③(2m＋ 1)(2m－1)； ④(5y ＋ z)(5y－z).
计算下列多项式的积，你能发现什么规律？
算一算：看谁算得又快又准.
②（m＋ 2)( m－2）=m2－22
③（2x＋ 1)( 2x－1)=4m2 － 12
④（5y ＋ z)(5y－z)= 25y2 － z2
①（x ＋1)( x－1）=x2 － 1，
想一想：这些计算结果有什么特点？
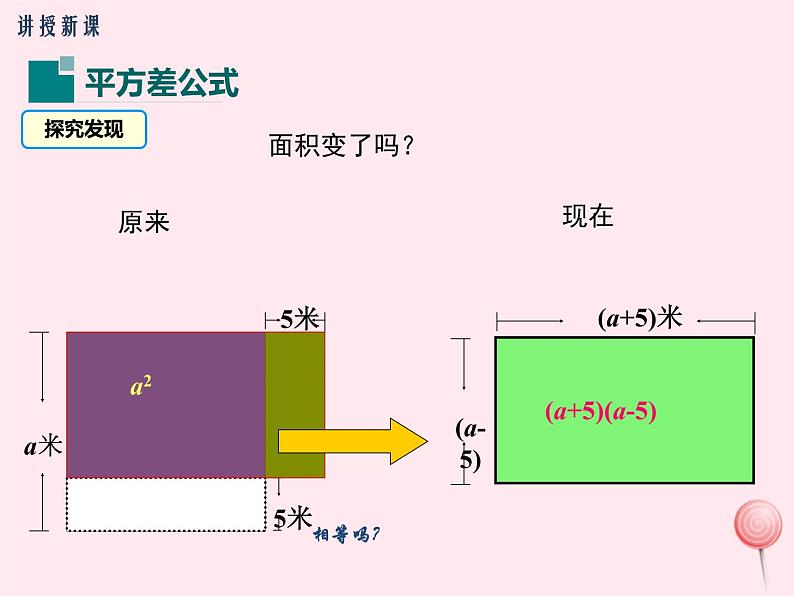
(a+b)(a−b)=
两数和与这两数差的积,等于这两数的平方差.这个公式叫做两数和与这两数差的乘法公式.有时也简称为平方差公式.
1.（a – b ) ( a + b) = a2 - b2
2.（b + a )( -b + a ) = a2 - b2
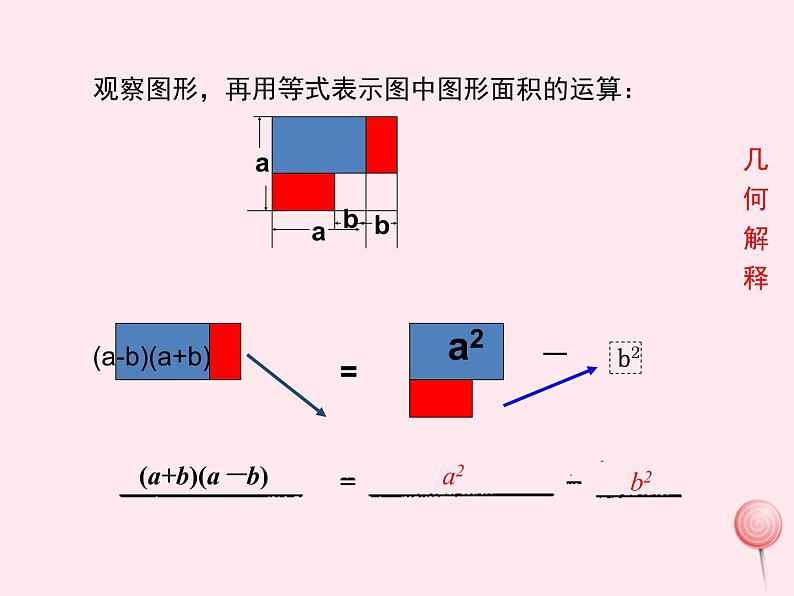
观察图形，再用等式表示图中图形面积的运算：
注：这里的两数可以是两个单项式,也可以是两个多项式等,．
(a+b)(a-b) = a2 - b2
练一练：口答下列各题： (l)(-a+b)(a+b)=  _________. (2)(a-b)(b+a)= __________. (3)(-a-b)(-a+b)= ________. (4)(a-b)(-a-b)= _________.
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
( 0.3x)2-12
例2 计算1998×2002.
（2000-2）（2000+2）
例3 街心花园有一块边长为a米的正方形草坪，经统一规划后，南北向要加长2米，而东西向要缩短2米，问改造后的长方形草坪的面积是多少？
答：改造后的长方形草坪的面积是(a2-4)平方米.
1.下面各式的计算对不对？如果不对，应当怎样改正？
（1）(x+2)(x-2)=x2-2
（2）(-3a-2)(3a-2)=9a2-4
（1）(x+2)(x-2)=x2-4
(-3a-2)(3a-2)=-[(3a+2)(3a-2)]=-(9a2-4)=-9a2+4;
(-3a-2)(3a-2)=(-2-3a)(-2+3a)=(-2)2-(3a)2=4-9a2.
（1）(a+3b)(a- 3b)；
=(2a+3)(2a-3)
=(-2x2 )2－y2
=(50+1)(50-1)
－(6x2+5x -6)
=3x2－5x－ 10.
（2）(3+2a)(－3+2a)；
（5）(3x+4)(3x-4)-(2x+3)(3x-2).
（4）(－2x2－y)(－2x2+y)；
2.利用平方差公式计算：
3.计算： 20152 － 2014×2016.
20152 － 2014×2016
= 20152 － (2015－1)(2015+1)
－ （20152－12 )
－ 20152+12
4.利用平方差公式计算:
（1）(a-2)(a+2)(a2 + 4) 解:原式=(a2-4)(a2+4) =a4-16.
（2）(x-y)(x+y)(x2+y2)(x4+y4).
解：原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.