初中数学华师大版八年级上册12.5 因式分解图片ppt课件

这是一份初中数学华师大版八年级上册12.5 因式分解图片ppt课件，共19页。PPT课件主要包含了因式分解，整式乘法，相同因式p，pa+pb+pc等内容，欢迎下载使用。

1.理解因式分解的意义和概念及其与整式乘法的区别和联系.（重点）2.理解并掌握提公因式法并能熟练地运用提公因式法分解因式.（难点）
运用前面所学的知识填空：
(1) m(a+b+c)= ； (2) (x+1)(x-1)= ；(3) (a+b)2 = .
把下列多项式写成乘积的形式
(1) ma+mb+mc=( )( )(2) x2 -1 =( )( ) (3) a2 +2ab+b2 =( )2
定义： 把一个多项式化为几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解，也叫做把这个多项式分解因式.
x2-1 (x+1)(x-1)
x2-1 = (x+1)(x-1)
等式的特征：左边是多项式，右边是几个整式的乘积
想一想：整式乘法与因式分解有什么关系？
在下列等式中，从左到右的变形是因式分解的有 ，不是的，请说明原因.
am+bm+c=m(a+b)+c
24x2y=3x ·8xy
x2-1=(x+1)(x-1)
(2x+1)2=4x2+4x+1
x2+x=x2(1+ )
2x+4y+6z=2(x+2y+3z)
因式分解的对象是多项式，而不是单项式
多项式中各项都含有的相同因式，叫做这个多项式的公因式.
这个多项式有什么特点？
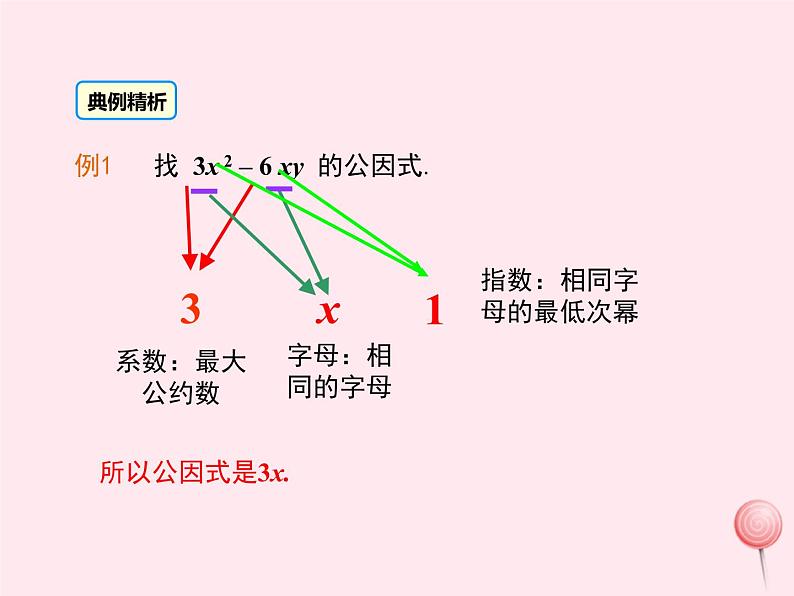
例1 找 3x 2 – 6 xy 的公因式.
指数：相同字母的最低次幂
正确找出多项式各项公因式的关键是：
1.定系数：公因式的系数是多项式各项系数的最大公约数. 2.定字母： 字母取多项式各项中都含有的相同的字母. 3.定指数：相同字母的指数取各项中最小的一个，即字母最低次幂.
一般地，如果多项式的各项有公因式，可以把这个公因式提取出来，将多项式写成公因式与另一个因式的乘积的形式，这种分解因式的方法叫做提公因式法.
( a+b+c )
找一找: 下列各多项式的公因式是什么？
(1) 3x+6y(2)ab-2ac(3) a 2 - a 3(4)4 (m+n) 2 +2(m+n)(5)9 m 2n-6mn (6)-6 x 2 y-8 xy 2
(1) 8a3b2 + 12ab3c；
例2 把下列各式分解因式：
分析：提公因式法步骤（分两步） 第一步:找出公因式； 第二步:提取公因式 ，即将多项式化为两个因式的乘积.
(2) 2a(b+c) - 3(b+c).
注意：公因式既可以是一个单项式的形式，也可以是一个多项式的形式.
整体思想是数学中一种重要而且常用的思想方法.
解：（1） 8a3b2 + 12ab3c=4ab2 ·2a2+4ab2 ·3bc=4ab2(2a2+3bc)；
如果提出公因式4ab,另一个因式是否还有公因式？
另一个因式将是2a2b+3b2c,
（2） 2a(b+c)-3(b+c)=(b+c)(2a-3).
如何检查因式分解是否正确？
正确解：原式=6xy(2x+3y).
当多项式的某一项和公因式相同时，提公因式后剩余的项是1.
注意：某项提出莫漏1.
正确解：原式=3x·x-6y·x+1·x =x(3x-6y+1).
提出负号时括号里的项没变号
注意：首项有负常提负.
正确解：原式= - (x2-xy+xz) =- x(x-y+z)
1.把下列各式分解因式：
(1)8 m2n+2mn；(2)12xyz-9x2y2；(3)p(a2 + b2 )- q(a2 + b2 )； (4) -x3y3-x2y2-xy.
3xy(4z-3xy)；
(a2+b2)(p-q)；
-xy(x2y2+xy+1).
2.分解因式：(x-y)2+y(y-x).
解法1：(x-y)2+y(y-x) =（x-y）2-y(x-y) =(x-y)(x-y-y) =(x-y)(x-2y).
解法2：(x-y)2+y(y-x) =（y-x)2+y(y-x) =(y-x)(y-x+y) =(y-x)(2y-x).
99 × 99 + 99
= 99 ×(99+1)
4.计算（-2）101+（-2）1005.已知: 2x+y=4,xy=3,求代数式2x2y+xy2的值.
解：原式=（-2）100 ×（-2+1） =2100 ×（-1） =-2100.
解：2x2y+xy2=xy(2x+y)=3 ×4=12.