湘教版八年级下册2.2 平行四边形综合与测试说课ppt课件

这是一份湘教版八年级下册2.2 平行四边形综合与测试说课ppt课件，共20页。PPT课件主要包含了第2章四边形，2平行四边形，知识目标，图2－2－12，图2－2－13，总结反思，图2－2－14等内容，欢迎下载使用。

第2课时 利用对角线的关系判定平行四边形
1．结合平行四边形对角线的性质，从对角线互相平分的角度去判定平行四边形，并能进行有关的证明与计算．2．通过求平行四边形两组对角的数量关系，归纳出“两组对角分别相等的四边形是平行四边形”这一判定方法，并能进行有关的证明和计算．3．回顾总结平行四边形的判定定理，能选择合适的方法判定平行四边形．
目标一　理解并会应用“对角线互相平分的四边形是平行四边形”
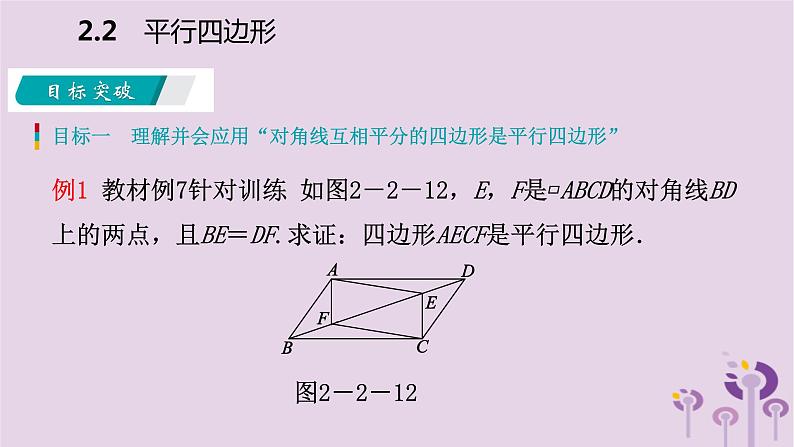
例1 教材例7针对训练 如图2－2－12，E，F是▱ABCD的对角线BD上的两点，且BE＝DF.求证：四边形AECF是平行四边形．
[解析] 连接AC，与BD相交于点O，发现▱ABCD与四边形AECF有一条公共对角线AC，而AC与BD互相平分，若能证明AC与EF也互相平分，则问题得证．而要证明AC与EF互相平分，即证明OA＝OC，OE＝OF，而OA＝OC可由▱ABCD的性质得到，即只需证OE＝OF.
证明：连接AC交BD于点O.∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD.∵BE＝DF，即OB＋OE＝OF＋OD，∴OE＝OF.又∵OA＝OC，∴四边形AECF是平行四边形．
【归纳总结】 当已知条件与所证四边形的对角线相关时，可利用“对角线互相平分的四边形是平行四边形”来证明一个四边形是平行四边形．
目标二　理解并会应用“两组对角分别相等的四边形是平行四边形”
例2　教材补充例题 下列给出的是四边形ABCD中∠A，∠B，∠C，∠D的度数之比，其中能说明四边形ABCD为平行四边形的是(　　)A．1∶2∶3∶4 B．2∶2∶3∶4C．2∶3∶2∶3 D．2∶3∶3∶2
[解析] C　由“两组对角分别相等的四边形是平行四边形”，可知C正确．
【归纳总结】 平行四边形的两组对角分别相等，反之，利用一个四边形两组对角分别相等这一关系也可以证明一个四边形是平行四边形．
目标三　能选择合适的方法判定平行四边形
例3 教材补充例题 如图2－2－13，四边形ABCD是平行四边形，E，F是对角线AC上的两点，∠1＝∠2.求证：(1)AE＝CF；(2)四边形EBFD是平行四边形．
[解析] (1)通过证明△CBF≌△ADE得到AE＝CF；或利用平行四边形对角线的性质，连接BD交AC于点O，证明△DOE≌△BOF，从而得出AE＝CF.(2)根据平行四边形的判定定理：一组对边平行且相等的四边形是平行四边形证得结论；或利用两组对边分别相等的四边形是平行四边形；或利用对角线互相平分的四边形是平行四边形证明．
证明：(1)(法一)如图①.∵四边形ABCD是平行四边形，∴AD＝CB，AD∥CB，∴∠3＝∠4.∵∠1＝∠3＋∠5，∠2＝∠4＋∠6，∠1＝∠2，∴∠5＝∠6，∴△ADE≌△CBF，∴AE ＝CF.(法二)如图②，连接BD交AC于点O.在▱ABCD中，OA＝OC，OB＝OD.∵∠1＝∠2，∠7＝∠8，∴△DOE≌△BOF，∴OE＝OF，∴OA－OE ＝OC－OF，即AE＝CF.
(2)(法一)如图①，∵∠1＝∠2，∴DE∥BF.由(1)得△ADE≌△CBF，∴DE＝BF，∴四边形EBFD是平行四边形．(法二)如图①，∵四边形ABCD是平行四边形，∴AB∥DC，AB＝DC，∴∠BAE＝∠DCF.又∵AE＝CF，∴△ABE≌△CDF，∴BE＝DF.由(1)得△ADE≌△CBF，∴DE＝BF，∴四边形EBFD是平行四边形．
(法三)如图②，连接BD交AC于点O.∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD.∵AE＝CF，∴OA－AE＝OC－CF，即OE＝OF.又∵OB＝OD，∴四边形EBFD是平行四边形．
【归纳总结】 平行四边形的判定
知识点一　平行四边形的判定定理3
__________________的四边形是平行四边形．
知识点二　平行四边形的判定方法
判定一个四边形是平行四边形有四种方法：①两组对边分别________的四边形是平行四边形(定义法)；②一组对边________且________的四边形是平行四边形(判定定理1)；③两组对边分别________的四边形是平行四边形(判定定理2)；④对角线互相________的四边形是平行四边形(判定定理3)．
[说明] 两组对角分别相等的四边形也是平行四边形．
知识点三　平行四边形的性质与判定的比较
如图2－2－14，AB，CD相交于点O，AC∥DB，OA＝OB，E，F分别为OC，OD的中点，连接AF，BE.求证：AF∥BE.请你判断下面的证明是否有错误，如果有错误，请说明理由，并写出正确的证明过程．证明：连接AE，BF.∵OC＝OD，E，F分别为OC，OD的中点，∴OE＝OF.又∵OA＝OB，∴四边形AFBE是平行四边形，∴AF∥BE.