初中数学湘教版八年级下册2.2 平行四边形综合与测试授课ppt课件

这是一份初中数学湘教版八年级下册2.2 平行四边形综合与测试授课ppt课件，共14页。PPT课件主要包含了第2章四边形，2平行四边形，知识目标，图2－2－9，图2－2－10，总结反思，图2－2－11等内容，欢迎下载使用。

第1课时 利用边的关系判定平行四边形
1．通过自学阅读、操作、猜想、讨论，能够得到“一组对边平行且相等的四边形是平行四边形”这一判定定理，并能初步应用．2．在理解平行四边形性质的基础上，经过画图、猜想、推理，能够得到“两组对边分别相等的四边形是平行四边形”这一判定定理，并会初步应用．
目标一　理解并会用“一组对边平行且相等的四边形是平行四边形”
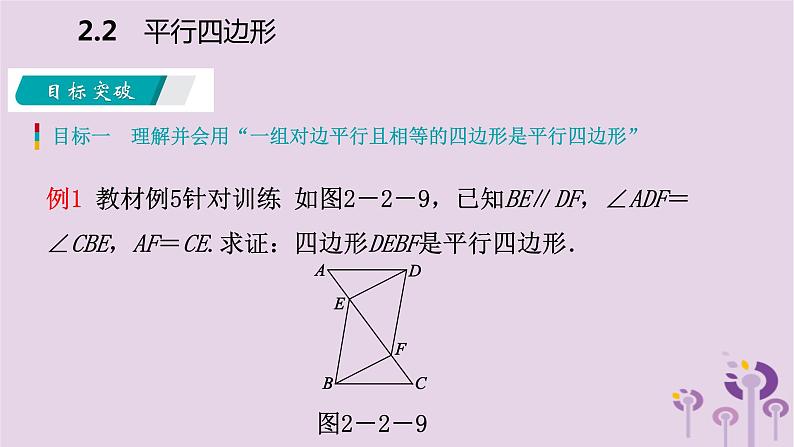
例1 教材例5针对训练 如图2－2－9，已知BE∥DF，∠ADF＝∠CBE，AF＝CE.求证：四边形DEBF是平行四边形．
[解析] 已知BE∥DF，所以只要通过证明△ADF≌△CBE，从而推出BE＝DF，即可利用一组对边平行且相等的四边形是平行四边形来证明．
证明：因为BE∥DF，所以∠AFD＝∠CEB.又因为∠ADF＝∠CBE，AF＝CE，所以△ADF≌△CBE，所以DF＝BE.又因为BE∥DF，所以四边形DEBF是平行四边形．
【归纳总结】 如果已知条件中有一组对边平行，可以尝试证明这一组对边相等(或另一组对边平行)，利用“一组对边平行且相等的四边形是平行四边形”(或定义)证明该四边形是平行四边形．
目标二　理解并会用“两组对边分别相等的四边形是平行四边形”
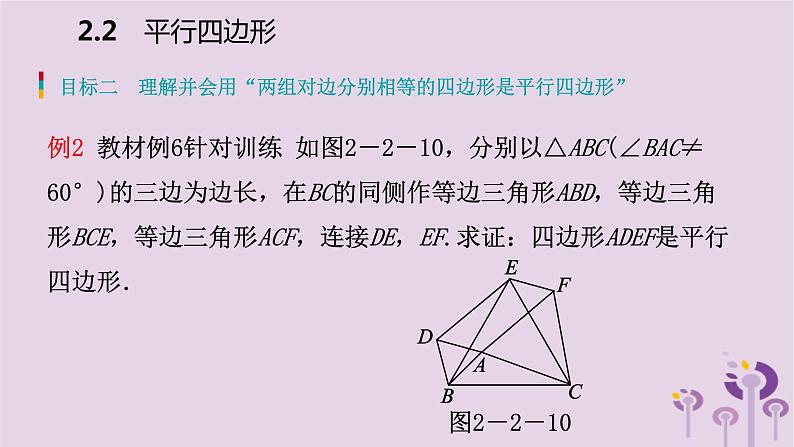
例2 教材例6针对训练 如图2－2－10，分别以△ABC(∠BAC≠60°)的三边为边长，在BC的同侧作等边三角形ABD，等边三角形BCE，等边三角形ACF，连接DE，EF.求证：四边形ADEF是平行四边形．
[解析] 证△EDB≌△CAB与△CFE≌△CAB可得BD＝EF＝DA，ED＝CF＝FA，所以ED＝FA，EF＝DA，所以四边形ADEF是平行四边形．
证明：因为△ABD，△BCE，△ACF均为等边三角形，所以BA＝BD＝DA，EB＝CB＝CE，CF＝FA＝AC，∠DBA＝∠EBC＝60°，所以∠DBE＋∠EBA＝∠ABC＋∠EBA＝60°，所以∠DBE＝∠ABC.在△EDB与△CAB中，因为BD＝BA，∠DBE＝∠ABC，EB＝CB，所以△EDB≌△CAB.同理可证△CFE≌△CAB，所以△EDB≌△CFE，所以BD＝EF＝DA，ED＝CF＝FA，所以ED＝FA，EF＝DA，所以四边形ADEF是平行四边形．
【归纳总结】 若已知条件中有一组对边相等，则可以尝试证明另一组对边也相等或证明这一组对边平行，从而证明该四边形是平行四边形．
知识点一　平行四边形的判定定理1
一组对边________且________的四边形是平行四边形．用几何语言叙述：在四边形ABCD中，若AB∥CD且AB＝CD，则四边形ABCD是平行四边形．
知识点二　平行四边形的判定定理2
两组对边分别________的四边形是平行四边形．用几何语言叙述：在四边形ABCD中，若AB＝CD且AD＝BC，则四边形ABCD是平行四边形．
[点拨] 连接一条对角线，利用全等三角形的判定与性质即可证明该定理．
如图2－2－11，在▱ABCD中，E是AB的中点，F是CD的中点．求证：四边形AECF是平行四边形．请你判断下面的证明过程是否正确，并说明理由．证明：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD.∵E，F分别是AB，CD的中点，∴DF＝BE.又∵∠D＝∠B，AD＝CB，∴△ADF≌△CBE，∴AF＝CE.又∵AE∥CF，∴四边形AECF是平行四边形．