湘教版八年级上册1.3.3整数指数幂的运算法则教课内容课件ppt

这是一份湘教版八年级上册1.3.3整数指数幂的运算法则教课内容课件ppt，共18页。PPT课件主要包含了学习目标，导入新课，回顾与思考，由此可以得出，讲授新课，2a-3-2，a7+-3，a5b-1，典例精析，做一做等内容，欢迎下载使用。

1.理解整数指数幂的运算法则；（重点）2.会用整数指数幂的运算法则进行计算.（重点、难点）
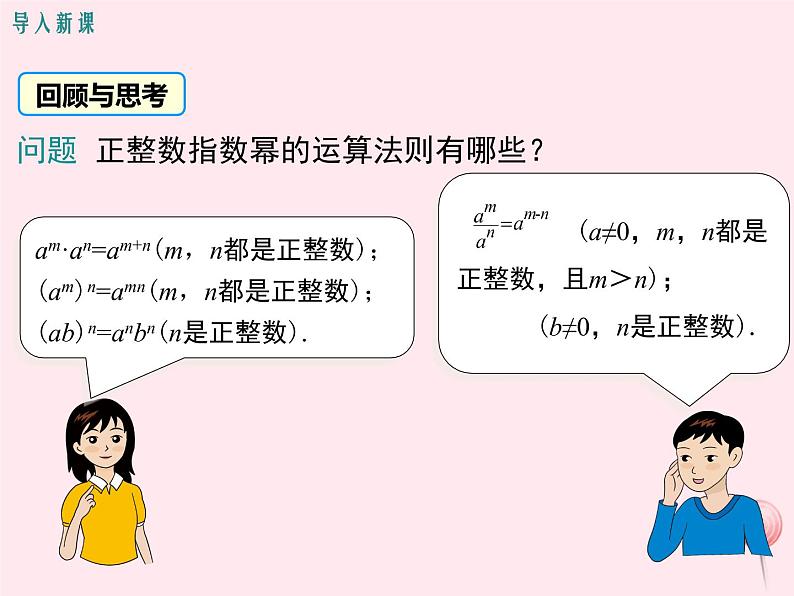
问题 正整数指数幂的运算法则有哪些？
am·an=am+n(m，n都是正整数)；(am)n=amn(m，n都是正整数)；(ab)n=anbn(n是正整数).
(a≠0，m，n都是正整数，且m＞n)； (b≠0，n是正整数).
思考:之前我们已经学习了零指数幂和负指数幂的运算，那么 am·an=am+n(m，n都是正整数)这条性质能否扩大到m，n都是任意整数的情形?
计算：(1)a3·a-5； （2）a-3·a-5；（3）a0·a-5.
am · an=am+n(a≠0，m，n都是整数)
引入负整数指数幂后，指数的取值范围就推广到全体整数.也就说前面提到的运算性质也推广到整数指数幂.
实际上，对于a≠0，m，n都是整数，有
因此，同底数幂相除和运算法则被包含在公式①中. 而对于a≠0，b≠0，n是整数，有
因此，分式的乘方的运算法则被包含在公式③中.
例1 设a≠0，b≠0，计算下列各式： （1）a7 · a-3；　 （2）(a-3)-2； （3）a3b(a-1b)-2.
解：（1） a7·a-3
= a(-3)×(-2)
（3） a3b(a-1b)-2
= a3b·a2b-2
= a3+2b1+(-2)
注意：最后结果一般不保留负指数，应写成分式形式.
例2 计算下列各式：
计算：(1)(x3y－2)2； (2)x2y－2·(x－2y)3；
解析：先进行幂的乘方，再进行幂的乘除，最后将整数指数幂化成正整数指数幂．
解：(1)原式＝x6y－4
(2)原式＝x2y－2·x－6y3＝x－4y
提示：计算结果一般需化为正整数幂的形式.
计算：(3)(3x2y－2)2÷(x－2y)3； (4)(3×10－5)3÷(3×10－6)2.
(4)原式＝(27×10－15)÷(9×10－12)＝3×10－3
解：(3)原式＝9x4y－4÷x－6y3＝9x4y－4·x6y－3＝9x10y－7
例4 已知a－m＝3，bn＝2，则(a－mb－2n)－2＝____．
解析：(a－mb－2n)－2＝(a－m)－2·b4n ＝(a－m)－2(bn)4 ＝3－2×24 ＝
方法总结：把要求的代数式逆用幂的运算法则，用已知的式子来表示是解题的关键．
例5 某房间空气中每立方米含3×106个病菌，为了试验某种杀菌剂的效果，科学家们进行实验，发现1毫升杀菌剂可以杀死2×105个这种病菌，问要将长10m，宽8m，高3m的房间内的病菌全部都杀死，需要多少杀菌剂？
解：（10×8×3）×（3×106）÷（2×105） =（720×106）÷（2×105） =360×10=3.6×103（毫升）.
1. 设a≠0，b≠0，计算下列各式：
（4）a-5(a2b-1)3=_________；
2. 计算下列各式：