初中数学湘教版八年级上册2.2 命题与证明背景图ppt课件

这是一份初中数学湘教版八年级上册2.2 命题与证明背景图ppt课件，共23页。PPT课件主要包含了学习目标，观察与思考，∠3≈1382，∠1≈1056，∠2≈1185，证明如图，第一步，第二步，第三步，画出图形等内容，欢迎下载使用。

1.了解证明的基本步骤和书写格式;（重点）2.掌握反证法证明的基本步骤和格式；（难点）3.掌握三角形外角和定理的证明，并能进行简单的运用.
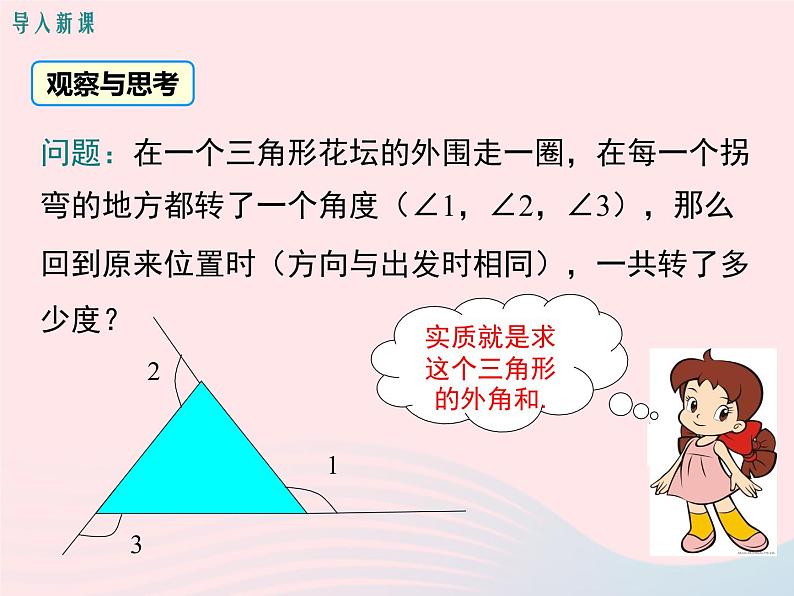
问题：在一个三角形花坛的外围走一圈，在每一个拐弯的地方都转了一个角度（∠1，∠2，∠3），那么回到原来位置时（方向与出发时相同），一共转了多少度？
实质就是求这个三角形的外角和.
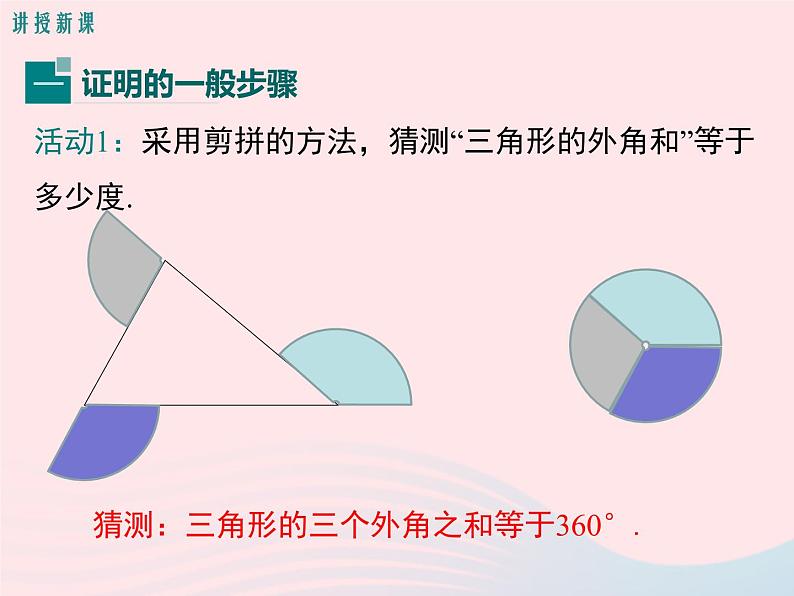
活动1：采用剪拼的方法，猜测“三角形的外角和”等于多少度.
猜测：三角形的三个外角之和等于360°.
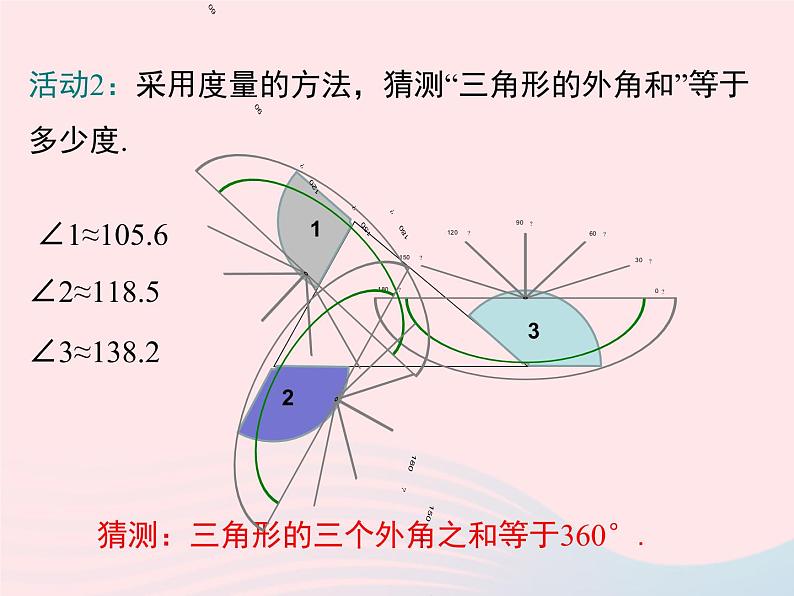
活动2：采用度量的方法，猜测“三角形的外角和”等于多少度.
从剪拼或度量可以猜测三角形的三个外角之和等于360°，但是剪拼时难以真正拼成一个周角，只是接近周角；分别度量这三个角后再相加，结果可能接近360°，但不能很准确地都得到360°.
思考：怎么证明“三角形的外角和为360°”呢？
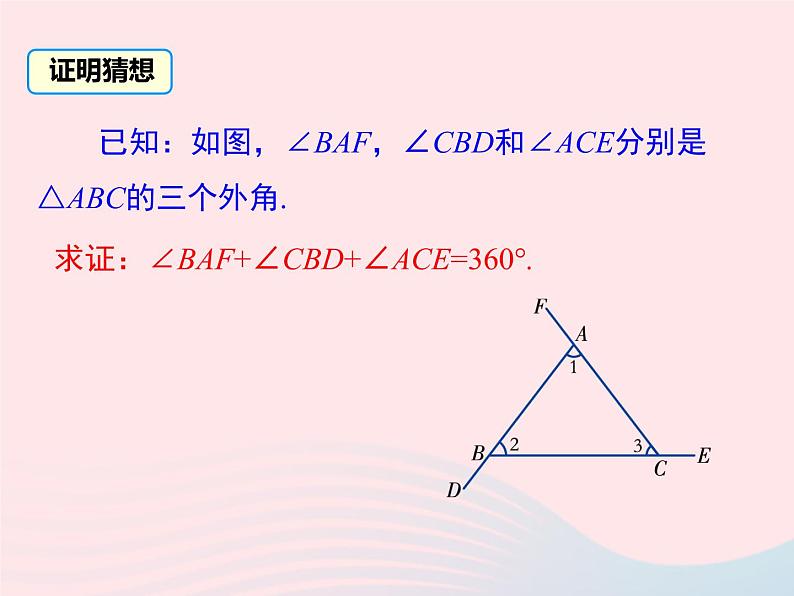
已知：如图，∠BAF，∠CBD和∠ACE分别是△ABC的三个外角.
求证：∠BAF+∠CBD+∠ACE=360°.
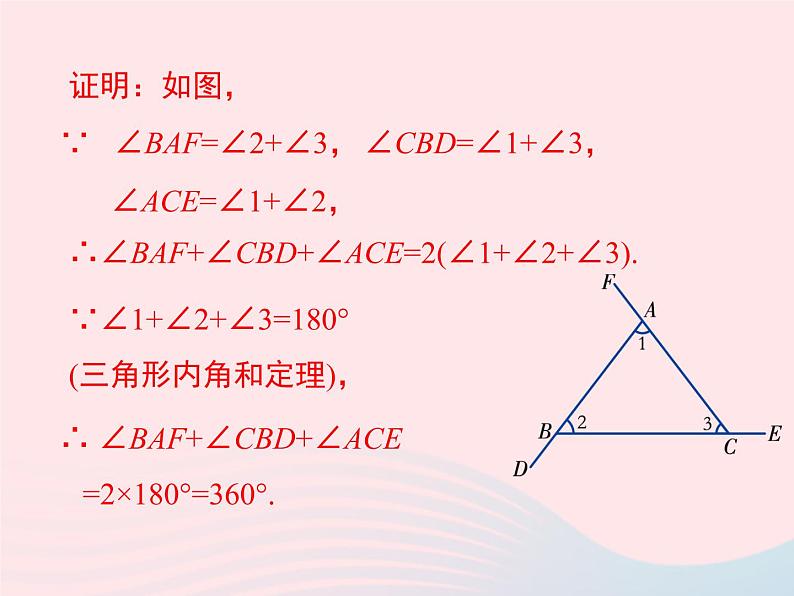
∵ ∠BAF=∠2+∠3，
∴∠BAF+∠CBD+∠ACE=2(∠1+∠2+∠3).
∠CBD=∠1+∠3，
∠ACE=∠1+∠2，
∵∠1+∠2+∠3=180°(三角形内角和定理)，
∴ ∠BAF+∠CBD+∠ACE =2×180°=360°.
证明与图形有关的命题时，一般有以下步骤：
例1 已知：如图，在△ABC中，∠B=∠C，点D在线段BA 的延长线上，射线AE平分∠DAC.
证明：∵∠DAC =∠B +∠C（三角形外角定理），
∴ ∠DAC=2∠B（等式的性质）.
又∵AE平分∠DAC（已知），
∴∠DAC=2∠DAE（角平分线的定义）
∴∠DAE=∠B（等量代换）.
∴AE∥BC（同位角相等，两直线平行）
例2 已知：∠A，∠B，∠C是△ABC的内角.
求证：∠A，∠B，∠C中至少有一个角大于或等于60°.
解析：这个命题的结论是“至少有一个”，也就是说可能出现“有一个” “有两个” “有三个”这三种情况. 如果直接来证明，将很繁琐，因此，我们将从另外一个角度来证明.
证明：假设∠A，∠B，∠C 中没有一个角大于或等于60°，
即∠A＜60°，∠B＜60°，∠C＜60°，
则∠A+∠B+∠C＜180°.
这与“三角形的内角和等于180°”矛盾，
因此，∠A， ∠B， ∠C中至少有一个角大于或等于60°.
像这样，先假设命题不成立，然后利用命题的条件或有关的结论，通过推理导出矛盾，从而得出假设不成立，即所证明的命题正确，这种证明方法称为反证法.
反证法是一种间接证明的方法，其基本的思路可归结为“否定结论，导出矛盾，肯定结论”.
应用反证法的情形：(1) 直接证明困难;(2) 需分成很多类进行讨论;(3) 结论为“至少”、“至多”、“有无穷多个” 的一类命题； (4) 结论为 “唯一”类命题.
用反正法证明时，导出矛盾的几种可能：
（1）与原命题的条件矛盾；
（3）与定义、公理、定理、性质矛盾；
（4）与客观事实矛盾.
命题“三角形中最多只有一个内角是直角”的结论的否定是(　　)A．两个内角是直角B．有三个内角是直角C．至少有两个内角是直角D．没有一个内角是直角
【解析】“最多只有一个”即为“至多一个”，反设应为“至少有两个”，故应选C.
1. 在括号内填上理由.
已知：如图，∠A+∠B= 180°.求证：∠C+∠D= 180°.证明：∵∠A+∠B= 180°（已知）， ∴ AD∥BC（ ）. ∴ ∠C+∠D= 180° （ ）.
同旁内角互补，两直线平行
两直线平行，同旁内角互补
2．应用反证法推出矛盾的推导过程中，要把下列哪些作为条件使用 (　　)①结论相反判断，即假设　②原命题的结论③公理、定理、定义等　　④原命题的条件A．①④　　　　　　　　B．①②③C．①③④ D．②③
3. 已知：如图，直线AB，CD被直线MN所截，∠1=∠2.求证：∠2=∠3，∠3+∠4=180°.
证明： ∵ ∠1=∠2，
∴ ∠2 =∠3（两直线平行,内错角相等）
∠3+∠4=180°（两直线平行, 同旁内角互补）.
∴ AB∥CD（同位角相等，两直线平行）
4. 已知：如图，AB与CD 相交于点E. 求证：∠A+∠C=∠B+∠D.
证明： ∵ AB与CD 相交于点E ，
∴ ∠AEC=∠BED （对顶角相等），
又 ∵∠A+∠C +∠AEC =∠B+∠D +∠BED =180°（三角形内角和等于180°），
5.求证：△ABC中不能有两个钝角．
证明：假设△ABC中能有两个钝角，即∠A＜90°，∠B＞90°，∠C＞90°， 所以∠A＋∠B＋∠C＞180°，与三角形的内角和为180°矛盾， 所以假设不成立，因此原命题正确，即△ABC中不能有两个钝角．