初中数学人教版八年级上册第十二章 全等三角形综合与测试精品当堂达标检测题

这是一份初中数学人教版八年级上册第十二章 全等三角形综合与测试精品当堂达标检测题，共16页。试卷主要包含了5B．1C．1等内容，欢迎下载使用。

基础过关


满分120分 时间100分钟


一．选择题（每题3分，共计30分）


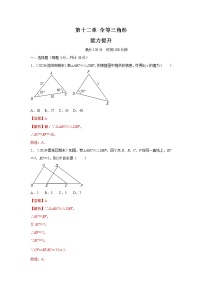
1.（2020•石台县期末）已知图中的两个三角形全等，则∠1等于（ ）





A．70°B．50°C．60°D．120°


【答案】C


【解答】∵△ABC≌△DEF，


∴∠E＝∠B＝70°，


∴∠1＝180°﹣50°﹣70°＝60°，


故选：C．





2．（2020•无棣县期末）如图，△ABC≌△ADE，点D落在BC上，且∠EDC＝70°，则∠BAD的度数等于（ ）





A．50°B．55°C．65°D．70°


【答案】D


【解答】∵△ABC≌△ADE，


∴AB＝AD，∠B＝∠ADE，


∴∠B＝∠ADB，


∴∠BDA＝∠ADE，


∵∠EDC＝70°，


∴∠BDA＝∠ADE=12×（180°﹣70°）＝55°．


∴∠BAD＝180°﹣55°﹣55°＝70°，


故选：D．


3．（2020 •历城区期中）如图，要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使BC＝CD，再作出BF的垂线DE，使点A、C、E在同一条直线上（如图），可以说明△ABC≌△EDC，得AB＝DE，因此测得DE的长就是AB的长，判定△ABC≌△EDC，最恰当的理由是（ ）





A．SASB．HLC．SSSD．ASA


【答案】D


【解答】因为证明在△ABC≌△EDC用到的条件是：CD＝BC，∠ABC＝∠EDC＝90°，∠ACB＝∠ECD，


所以用到的是两角及这两角的夹边对应相等即ASA这一方法．


故选：D．


4．（2020•五常市期末）如图所示，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，DE＝4，BC＝9，则BD的长为（ ）





A．6B．5C．4D．3


【答案】B


【解答】∵AD平分∠BAC，DE⊥AB，DC⊥AC，


∴DC＝DE＝4，


∴BD＝BC﹣CD＝9﹣4＝5．


故选：B．


5．（2020 •南岗区期末）如图，已知∠l＝∠4，添加以下条件，不能判定△ABC≌△CDA的是（ ）





A．∠2＝∠3B．∠B＝∠DC．BC＝DAD．AB＝DC


【答案】D


【解答】A、∵在△ABC和△CDA中


∠1=∠4AC=CA∠3=∠2，


∴△ABC≌△CDA（ASA），故本选项不符合题意；


B、∵在△ABC和△CDA中


∠1=∠4∠B=∠DAC=CA，


∴△ABC≌△CDA（AAS），故本选项不符合题意；


C、∵在△ABC和△CDA中


BC=DA∠1=∠4AC=CA，


∴△ABC≌△CDA（SAS），故本选项不符合题意；


D、根据AB＝AC，AC＝AC和∠1＝∠4不能推出△ABC≌△CDA，故本选项符合题意；


故选：D．





6．（2020•蜀山区期末）如图，D是AB延长线上一点，DF交AC于点E，AE＝CE，FC∥AB，若AB＝3，CF＝5，则BD的长是（ ）





A．0.5B．1C．1.5D．2


【答案】D


【解答】证明：∵FC∥AB


∴∠FCE＝∠DAE，


在△CFE和△ADE中


∠FCE=∠DAECE=AE∠CEF=∠AED，


∴△CFE≌△ADE（ASA），


∴AD＝CF＝5，


∵AB＝3，


∴BD＝5﹣3＝2，


故选：D．


7．（2020•曹县期末）如图，点O在AD上，∠A＝∠C，∠AOC＝∠BOD，AB＝CD，AD＝6cm，OC＝4cm，则OB的长为（ ）





A．2cmB．3cmC．4cmD．6cm


【答案】A


【解答】∵∠AOC＝∠BOD，


∴∠AOB＝∠COD，


∵∠A＝∠C，CD＝AB，


∴△AOB≌△COD（AAS），


∴OA＝OC＝4cm，OB＝OD，


∵AD＝6cm，


∴OD＝AB﹣OA＝2cm，


∴OB＝OD＝2cm．


故选：A．


8．（2020•宁波模拟）如图，BD＝BC，BE＝CA，∠DBE＝∠C＝62°，∠BDE＝75°，则∠AFE的度数等于（ ）





A．148°B．140°C．135°D．128°


【答案】A


【解答】∵BD＝BC，BE＝CA，∠DBE＝∠C，


∴△ABC≌△EDB（SAS），


∴∠A＝∠E，


∵∠DBE＝62°，∠BDE＝75°，


∴∠E＝180°﹣60°﹣75°＝43°，


∴∠A＝43°，


∵∠BDE+∠ADE＝180°，


∴∠ADE＝105°，


∴∠AFE＝∠ADE+∠A＝105°+43°＝148°．


故选：A．


9．（2020•呼和浩特期末）图中的小正方形边长都相等，若△MNP≌△MFQ，则点Q可能是图中的（ ）





A．点DB．点CC．点BD．点A


【答案】A


【解答】观察图象可知△MNP≌△MFD．





故选：A．


10．（2020•偃师市期末）如图，BP平分∠ABC，D为BP上一点，E，F分别在BA，BC上，且满足DE＝DF，若∠BED＝140°，则∠BFD的度数是（ ）





A．40°B．50°C．60°D．70°


【答案】A


【解答】作DG⊥AB于G，DH⊥BC于H，


∵D是∠ABC平分线上一点，DG⊥AB，DH⊥BC，


∴DH＝DG，


在Rt△DEG和Rt△DFH中，


DG=DHDE=DF，


∴Rt△DEG≌Rt△DFH（HL），


∴∠DEG＝∠DFH，又∠DEG+∠BED＝180°，


∴∠BFD+∠BED＝180°，


∴∠BFD的度数＝180°﹣140°＝40°，


故选：A．





二．填空题（每题3分，共计15分）


11．（2020春•香坊区期末）如图，∠B＝∠C＝90°，AB＝AC，∠ADB＝65°，则∠DAC的度数为 ．





【答案】25


【解答】∵∠B＝∠C＝90°，AB＝AC，


在Rt△ABD与Rt△ACD中


AB=ACAD=AD，


∴Rt△ABD≌Rt△ACD（HL），


∴∠ADC＝∠ADB＝65°，


∴∠DAC＝90°﹣65°＝25°，


故答案为：25．


12．（2020•朝阳区模拟）如图所示的网格是正方形网格，图形的各个顶点均为格点，则∠1+∠2＝ ．





【答案】45°


【解答】如图所示：


由题意可得：∠1＝∠3，


则∠1+∠2＝∠2+∠3＝45°．


故答案为：45°．





13．（2020 •南岗区期中）如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，若△ABC的面积为21cm2，AB＝8cm，AC＝6cm，则DE的长为 cm．





【答案】3


【解答】∵AD为∠BAC的平分线，DE⊥AB，DF⊥AC，


∴DE＝DF，


∵S△ABD+S△ACD＝S△ABC，


∴12×AB×DE+12×DF×AC＝21，


即12×8×DE+12×DE×6＝21，


∴DE＝3（cm）．


故答案为3．


14．（2020•南江县期末）如图，△ABC的三边AB，BC，CA的长分别为30，40，15，点P是△ABC三个内角平分线的交点，则S△PAB：S△PBC：S△PCA＝ ．





【答案】6：8：3


【解答】∵点P是△ABC三个内角平分线的交点，


∴P点到三边的距离相等，


设这个距离为m，


∴S△PAB：S△PBC：S△PCA=12×AB×m-12×BC×m-12×AC×m


＝AB：BC：AC


＝30：40：15


＝6：8：3．


故答案为6：8：3．


15．（2020•永州期末）如图，在△ABC和△DBC中，∠A＝40°，AB＝AC＝2，∠BDC＝140°，BD＝CD，以点D为顶点作∠MDN＝70°，两边分别交AB，AC于点M，N，连接MN，则△AMN的周长为 4 ．





【答案】4


【解答】延长AC至E，使CE＝BM，连接DE．


∵BD＝CD，且∠BDC＝140°，


∴∠DBC＝∠DCB＝20°，


∵∠A＝40°，AB＝AC＝2，


∴∠ABC＝∠ACB＝70°，


∴∠MBD＝∠ABC+∠DBC＝90°，


同理可得∠NCD＝90°，


∴∠ECD＝∠NCD＝∠MBD＝90°，


在△BDM和△CDE中，BM=CE∠MBD=∠ECDBD=CD，


∴△BDM≌△CDE（SAS），


∴MD＝ED，∠MDB＝∠EDC，


∴∠MDE＝∠BDC＝140°，


∵∠MDN＝70°，


∴∠EDN＝70°＝∠MDN，


在△MDN和△EDN中，MD=ED∠MDN=∠EDNDN=DN，


∴△MDN≌△EDN（SAS），


∴MN＝EN＝CN+CE，


∴△AMN的周长＝AM+MN+AN＝AM+CN+CE+AN＝AM+AN+CN+BM＝AB+AC＝4；


故答案为：4．





三．解答题（共75分）


16．（8分）（2020•铜仁市期末）如图，∠A＝∠B＝90°，E是AB上的一点，且AD＝BE，∠1＝∠2，求证：Rt△ADE≌Rt△BEC．





证明：∵∠1＝∠2，


∴DE＝CE．


∵∠A＝∠B＝90°，


∴△ADE和△EBC是直角三角形，而AD＝BE．


∴Rt△ADE≌Rt△BEC（HL）


17．（9分）（2020•临泉县期末）如图，△ABC≌△DBE，点D在边AC上，BC与DE交于点P，已知∠ABE＝162°，∠DBC＝30°，求∠CDE的度数．





解：∵∠ABE＝162°，∠DBC＝30°，


∴∠ABD+∠CBE＝132°，


∵△ABC≌△DBE，


∴∠ABC＝∠DBE，∠C＝∠E，


∴∠ABD＝∠CBE＝132°÷2＝66°，


∵∠CPD＝∠BPE，


∴∠CDE＝∠CBE＝66°．


18．（9分）（2020•鼓楼区期末）如图，点C、F在线段BE上，∠ABC＝∠DEF＝90°，BC＝EF，请只添加一个合适的条件使△ABC≌△DEF．


（1）根据“ASA”，需添加的条件是 ；根据“HL”，需添加的条件是 ；


（2）请从（1）中选择一种，加以证明．





解：（1）根据“ASA”，需添加的条件是∠ACB＝∠DFE，根据“HL”，需添加的条件是AC＝DF，


故答案为：∠ACB＝∠DFE，AC＝DF；


（2）选择添加条件AC＝DE证明，


证明：∵∠ABC＝∠DEF＝90°，


∴在Rt△ABC和Rt△DEF中，


AC=DEBC=EF，


∴Rt△ABC≌Rt△DEF（HL）．


19．（9分）（2020•三台县期末）王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC＝BC，∠ACB＝90°），点C在DE上，点A和B分别与木墙的顶端重合．


（1）求证：△ADC≌△CEB；


（2）求两堵木墙之间的距离．





（1）证明：由题意得：AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，


∴∠ADC＝∠CEB＝90°，


∴∠ACD+∠BCE＝90°，∠ACD+∠DAC＝90°，


∴∠BCE＝∠DAC


在△ADC和△CEB中∠ADC=∠CEB∠DAC=∠BCEAC=BC，


∴△ADC≌△CEB（AAS）；


（2）解：由题意得：AD＝2×3＝6cm，BE＝7×2＝14cm，


∵△ADC≌△CEB，


∴EC＝AD＝6cm，DC＝BE＝14cm，


∴DE＝DC+CE＝20（cm），


答：两堵木墙之间的距离为20cm．


20．（10分）（2020•温州一模）如图，在△ABC中，AB＝AC，点D在BC边上，点E在AC边上，连结AD，DE．已知∠1＝∠2，AD＝DE．


（1）求证：△ABD≌△DCE．


（2）若BD＝2，CD＝5，求AE的长．





（1）证明：∵AB＝AC，


∴∠B＝∠C，


又∠1＝∠2，AD＝DE，


∴△ABD≌△DCE（AAS）；


（2）解：∵△ABD≌△DCE，


∴AB＝DC＝5，CE＝BD＝2，


∵AC＝AB，


∴AC＝5，


∴AE＝AB﹣EC＝5﹣2＝3．


21．（10分）（2020•扬中市模拟）如图，四边形ABCD中，对角线AC、BD交于点O，AB＝AC，点E是BD上一点，且∠ABD＝∠ACD，∠EAD＝∠BAC．


（1）求证：AE＝AD；


（2）若∠ACB＝65°，求∠BDC的度数．





证明：（1）∵∠BAC＝∠EAD


∴∠BAC﹣∠EAC＝∠EAD﹣∠EAC


即：∠BAE＝∠CAD


在△ABE和△ACD中


∠ABD=∠ACDAB=AC∠BAE=∠CAD，


∴△ABE≌△ACD（ASA），


∴AE＝AD；


（2）解：∵∠ACB＝65°，AB＝AC，


∴∠ABC＝∠ACB＝65°，


∴∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣65°﹣65°＝50°，


∵∠ABD＝∠ACD，∠AOB＝∠COD，


∴∠BDC＝∠BAC＝50°．


22.（10分）（2020 •南岗区期末）如图，△ABC的边AB与△EDC的边ED相交于点F，连接CF．已知AC＝EC，BC＝DC，∠BCD＝∠ACE．


（1）求证：AB＝ED；


（2）求证：FC平分∠BFE．





证明：（1）∵∠BCD＝∠ACE，


∴∠BCD+∠ACD＝∠ACE+∠ACD，


即∠BCA＝∠DCE，


在△ABC与△EDC中


BC=DC∠BCA=∠DCEAC=EC，


∴△ABC≌△EDC（SAS），


∴AB＝ED；


（2）过点C作CG⊥AB，CH⊥DE，垂足分别为G，H，


∵△ABC≌△EDC，


∴∠B＝∠D，


∵CG⊥AB，CH⊥DE，


∴∠BGC＝∠DHC＝90°，


在△BCG与△DCH中


∠B=∠D∠BGC=∠DHCBC=DC，


∴△BCG≌△DCH（AAS），


∴CG＝CH，


∴FC平分∠BFE．


23．（11分）（2020•内乡县期末）如图（1），AB＝7cm，AC⊥AB，BD⊥AB垂足分别为A、B，AC＝5cm．点P在线段AB上以2cm/s的速度由点A向点B运动，同时点Q在射线BD上运动．它们运动的时间为t（s）（当点P运动结束时，点Q运动随之结束）．





（1）若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，并判断此时线段PC和线段PQ的位置关系，请分别说明理由；


（2）如图（2），若“AC⊥AB，BD⊥AB”改为“∠CAB＝∠DBA”，点Q的运动速度为xcm/s，其它条件不变，当点P、Q运动到何处时有△ACP与△BPQ全等，求出相应的x的值．


解：（1）△ACP≌△BPQ，PC⊥PQ．


理由如下：∵AC⊥AB，BD⊥AB，


∴∠A＝∠B＝90°，


∵AP＝BQ＝2，


∴BP＝5，


∴BP＝AC，


∴△ACP≌△BPQ（SAS）；


∴∠C＝∠BPQ，


∵∠C+∠APC＝90°，


∴∠APC+∠BPQ＝90°，


∴∠CPQ＝90°，


∴PC⊥PQ；


（2）①若△ACP≌△BPQ，


则AC＝BP，AP＝BQ，可得：5＝7﹣2t，2t＝xt


解得：x＝2，t＝1；


②若△ACP≌△BQP，


则AC＝BQ，AP＝BP，可得：5＝xt，2t＝7﹣2t


解得：x=207，t=74．


综上所述，当△ACP与△BPQ全等时x的值为2或207．