鲁教版 (五四制)八年级下册1 菱形的性质与判定一等奖ppt课件

这是一份鲁教版 (五四制)八年级下册1 菱形的性质与判定一等奖ppt课件，共21页。PPT课件主要包含了特殊的平行四边形，菱形的性质等内容，欢迎下载使用。

平行四边形的对边平行；
平行四边形的对边相等；
平行四边形的对角相等；
平行四边形的邻角互补；
平行四边形的对角线互相平分；
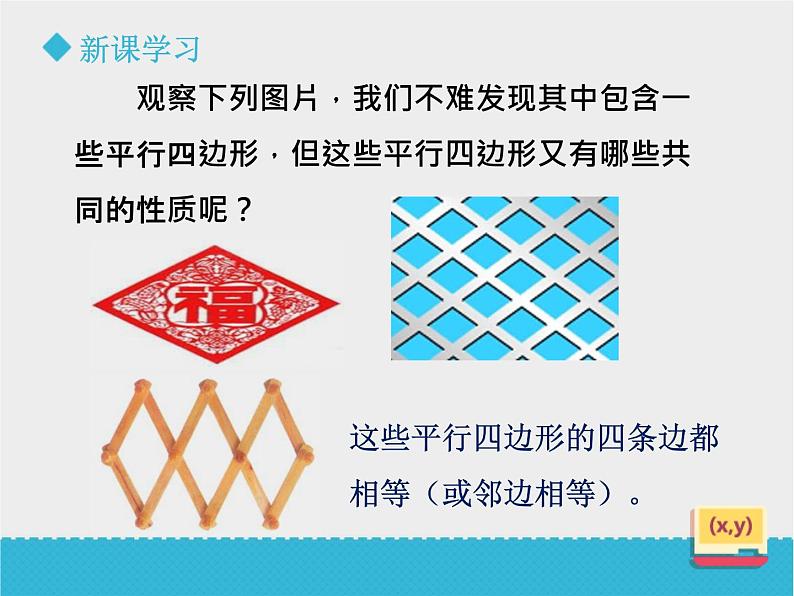
观察下列图片，我们不难发现其中包含一些平行四边形，但这些平行四边形又有哪些共同的性质呢？
这些平行四边形的四条边都相等（或邻边相等）。
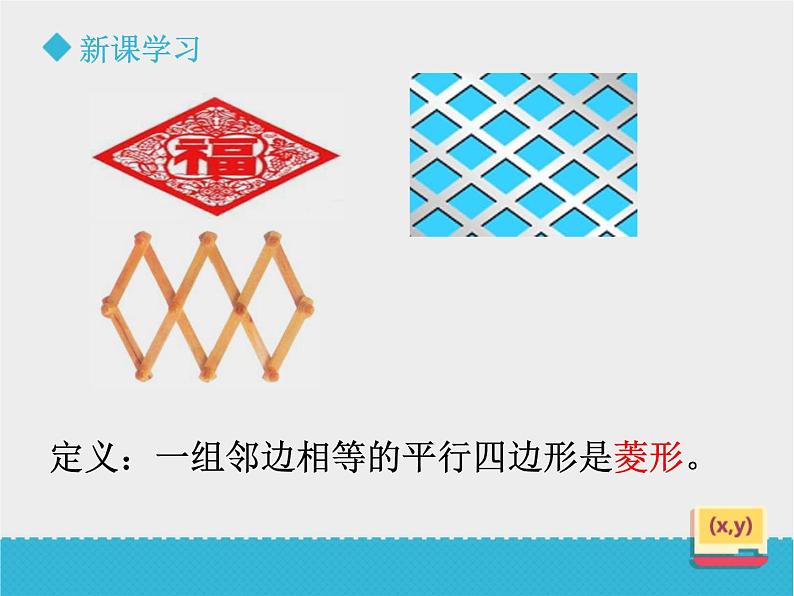
定义：一组邻边相等的平行四边形是菱形。
想一想：菱形是特殊的平行四边形，它具有一般的平行四边形的所有的性质，你能列举一些这样的性质吗？
菱形的对角线互相平分；
想一想：你认为菱形还有哪些性质？ （与同伴交流）
①菱形的四边相等；②菱形是轴对称图形，两条对角线所在直线都是它的对称轴；③菱形的对角线互相垂直。
做一做：用菱形的纸片折一折，回答问题：
１、菱形是轴对称图形吗？如果是，菱形有几条对称轴？对称轴之间有什么位置关系？
2、你能看出图中哪些线段和角相等？
菱形是轴对称图形，有两条对称轴，对称轴即为菱形的对角线，对称轴互相垂直。
AB=CD=AD=BC OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA ∠AOB=∠DOC=∠AOD=∠BOC =90° ∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB≌Rt△COB≌Rt△COD≌Rt△AOD△ABD≌△CBD △ABC≌△ADC
已知:如图，在菱形ABCD中，AB=AD，对角线AC与BD相交于点O。
证明：(1)∵四边形ABCD是菱形
∴AB=CD，AD=BC（菱形的对边相等）
∴AB=BC=DC=DA
(1)AB=BC=CD=AD
(2)AC⊥BD
证明：(2)∵AB=AD
又∵四边形ABCD是菱形
∴△ABD是等腰三角形
∴OB=OD（菱形的对角线互相平分）
定理：菱形的四条边都相等定理：菱形的对角线互相垂直
例1：如图，在菱形ABCD中，对角线AC与BD相交于点O，∠BAD=60°，BD=2，求AB与AC的长。
解：∵四边形ABCD是菱形，
∴AB=AD（菱形的四条边都相等） AC⊥BD（菱形的对角线互相垂直）
在等腰三角形ABD中，∵∠BAD=60°，
∴△ABD是等边三角形
在Rt△AOB中，由勾股定理，得：
OA²+OB²=AB²
性质：（1）菱形具有平行四边形的一切性质；
（2）菱形的四条边都相等；
（3）菱形的两条对角线互相垂直.
1、如图，在菱形ABCD中，对角线AC与BD相交于点O，已知AB=5cm，AO=4cm，求BD的长。
∴AC⊥BD（菱形的对角线互相垂直） OB=OD（菱形的对角线互相平分）
∴在Rt△AOB中，由勾股定理，得：
∵AB=5cm，AO=4cm
∴BD=2OB=2×3=6（cm）
2、菱形的两组对边的距离相等吗？为什么？
相等；原因： 菱形是特殊的平行四边形，所以菱形的面积等于底乘以高，菱形的底是菱形的边，菱形的高是菱形对边之间的距离；因为菱形四条边都相等，所以菱形的底相等，因此菱形的高也相等，即菱形的两组对边之间的距离相等。
课本第4页习题6.1第1、2、3、4题
菱形的性质定义：邻边相等 平行四边形性质：1、平行四边形的性质 2、四条边都相等 3、对角线互相垂直