




初中数学鲁教版 (五四制)八年级下册6 黄金分割备课ppt课件
展开一天,毕达哥拉斯从一家铁匠铺路过,被铺子中那有节奏的叮叮当当的打铁声所吸引,便站在那里仔细聆听,似乎这声音中隐匿着什么秘密。他走进作坊,拿出一把尺量了一下铁锤和铁砧的尺寸,发现它们之间存在着一种十分和谐的关系。回到家里,毕达哥拉斯拿出一根线,想将它分为两段。怎样分才最好呢?经过反复比较,他最后确定1:0.618的比例截断最优美。后来,德国的美学家泽辛把这一比例称为黄金分割律。这个规律的意思是,较大部分与整体这个比等于较小部分与较大部分之比。无论什么物体、图形,只要它各部分的关系都与这种分割法相符,这类物体、图形就能给人最悦目、最美的印象。
探索身边的“黄金分割”
为什么翩翩起舞的芭蕾舞演员要掂起脚? 为什么身材苗条的时装模特还要穿高跟鞋?为什么她们会给人感到和谐、平衡、舒适、美的感觉?
黄金分割又称黄金律,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值为1∶0.618或0.618∶1,即长段为全段的0.618。0.618被公认为最具有审美意义的比例数字。上述比例是最能引起人的美感的比例,因此被称为黄金分割。
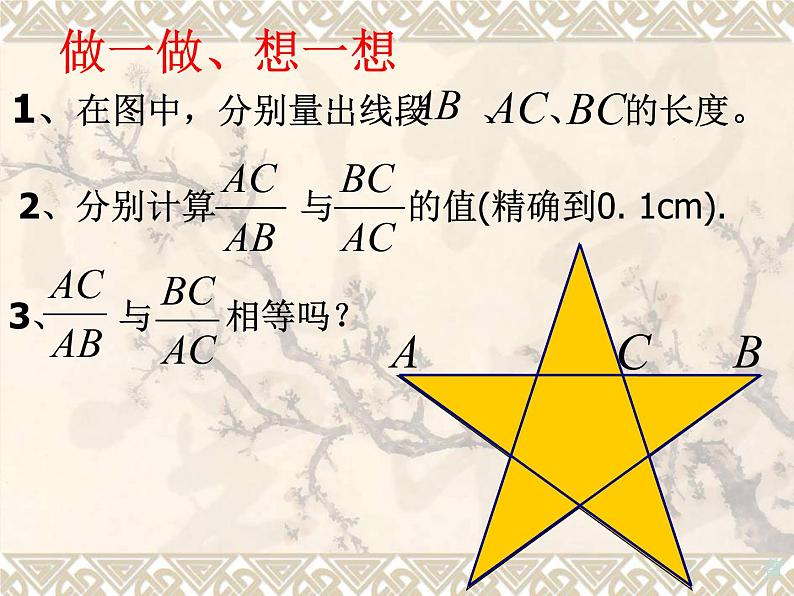
通过五角星例子来说明什么是黄金分割。
黄金分割 与生活
由黄金分割画出的正五角星形,有庄严雄健之美。
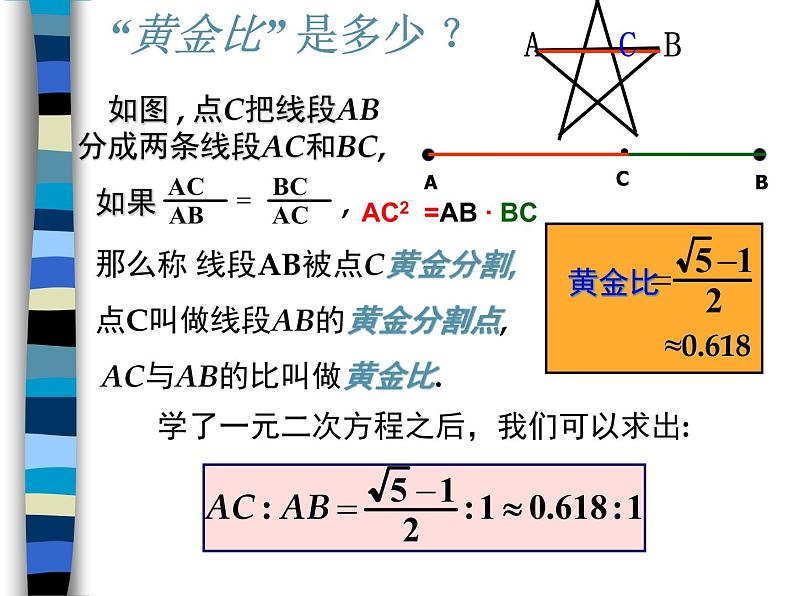
“黄金比” 是多少 ?
学了一元二次方程之后,我们可以求出:
如果 ,
那么称 线段AB被点C黄金分割,
点C叫做线段AB的黄金分割点,
AC与AB的比叫做黄金比.
点C把线段AB分成两条线段AC和BC,
AC2 =AB ∙ BC
1.如果设AB=2,那么BD,AD,AC,BC分别等于多少?
3.点C是线段AB的黄金分割点吗?
如图,乐器上的一根弦AB=80cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点。试确定支撑点C到端点B的距离以及支撑点D到端点A的距离。
巴台农神庙(Parthenm Temple)
1.点E是AB的黄金分割点吗?
2.矩形ABCD的宽与长的比是黄金比吗?
宽与长的比等于黄金比的矩形也称为黄金矩形
东方明珠塔,塔高462.85米。设计师将在295米处设计了一个上球体,使平直单调的塔身变得丰富多彩,非常协调、美观。
小提琴是一种造型优美、声音诱人的弦乐器,它的共鸣箱的一个端点正好是整个琴身的黄金分割点。
高雅的艺术殿堂里,自然也留下了黄金数的足迹。画家们发现,按0.618∶1来设计腿长与身高的比例,画出的人体身材最优美,而现今的女性,腰身以下的长度平均只占身高的0.58,因此古希腊维纳斯女塑像及太阳神阿波罗的形象都通过故意延长双腿,使之与身高的比值为0.618,从而创造艺术美。难怪许多姑娘都愿意穿上高跟鞋,而芭蕾舞演员则在翩翩起舞时,不时地踮起脚尖。
著名油画蒙娜丽莎的构图就完美的体现了黄金分割在油画艺术上的应用.通过上面两幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都完美的体现了黄金分割,使得这幅油画看起来是那么的和谐和完美.
1 :人体肚脐不但是美化身型的黄金点有时还是医疗效果黄金点,许多民间名医在肚脐上贴药治好了某些疾病。
2:人体最感舒适的温度是23℃,也是正常人体温(37℃)的黄金点(23=37×0.618)。
3:人体还有几个黄金点:肚脐上部分的黄金点在咽喉,肚脐以下部分的黄金点在膝盖,上肢的黄金点在肘关节。上肢与下肢长度之比均近似0.618.
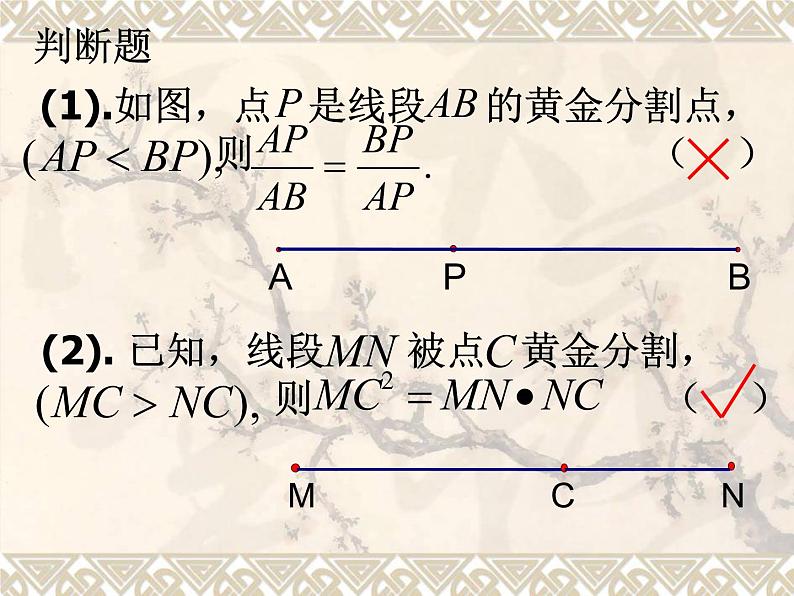
一、如图,已知C是线段AB的黄金分割点写出AC,BC,AB所成立的比例式
1、黄金分割就是一点将一条线段分成大小不等的两条线段。 ( )
2、若点C是线段AB的黄金分割点,且AC>BC,AB=L,则AC= L ( )
三、填空1、若点C是线段AB的黄金分割点,且AC>CB,则AC:AB= ____2、如果线段AB=10cm,点C是AB上的黄金分割点,且AC>BC,则AC之长是____ __cm.
本节课你学习到了哪些东西?
1.黄金分割点的定义及黄金比值
2.如何找一条线段的黄金分割点,以及会画黄金矩形
3.能根据定义判断某一点是否为一条线段的黄金分割点
如图, 设AB是已知线段, 在AB上作正方形ABCD ;取AD的中点E, 连接EB; 延长DA至F, 使EF=EB ;以线段AF为边作正方形AFGH .点H就是AB的黄金分割点 .
AE= ; EB= ;EF= ; AF= 。
所以, AH= ; HB= ;
因此, 点H就是AB的黄金分割点 .
打开地图,你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”,产地在安徽的祁门,也恰好在此纬度上。这不免让人联想起许多与北纬30度有关的地方。奇石异峰,名川秀水的黄山,庐山,九寨沟等等。衔远山、吞长江的中国三大淡水湖也恰好在这黄金分割的纬度上。
蝴蝶身长与双翅展开后的长度之比, 普通树叶的宽与长之比也接近0.618; 节目主持人报幕,绝对不会站在舞台的中央,而总是站在舞台的1/3处,站在舞台上侧近于0.618的位置才是最佳的位置; 生活中用的纸为黄金矩形,这样的长方形让人看起来舒服顺眼,正规裁法得到的纸张,不管其大小,如对于8开、16开、32开等,都仍然是近似的黄金矩形。
文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边长与高这比都接近于0.618.
古希腊的一些神庙,在建筑时高和宽也是按黄金比0.618来建立,他们认为这样的长方形看来是较美观;其大理石柱廓,就是根据黄金分割律分割整个神庙的.
雕塑断臂女神维纳斯的体型完全与黄金比相符,即以人的肚脐为分界点,上身与下身之比,或者说下身与全身之比约是0.618 这样的身体给人的感觉就是非常的匀称,充满着美感.
著名画家达•芬奇的蒙娜丽莎构图就完美的体现了黄金分割在油画艺术上的应用。通过下面两幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割,使得这幅油画看起来是那么的和谐和完美.
1.据有关测定,当气温处于人体正常体温(36 ℃ ~37℃)的黄金比值时,人体感到最舒适。因此夏天使用空调时室内温度调到什么温度最适合?
2.在人体下半身与身高的比例上,越接近 0.618, 越给人美感,遗憾的是,即使是身体修长的芭蕾舞演员也达不到如此的完美。某女士身高1.68米,下半身1.02米,她应该选择多高的高跟鞋看起来更美呢?
36℃×0.618=22.3 ℃37℃×0.618=22.8 ℃22.3 ℃~22.8℃
初中数学鲁教版 (五四制)八年级下册6 一元二次方程的应用教学演示课件ppt: 这是一份初中数学鲁教版 (五四制)八年级下册6 一元二次方程的应用教学演示课件ppt,共14页。PPT课件主要包含了回顾复习,一元二次方程的应用,例题解析,作业布置等内容,欢迎下载使用。
数学1 一元二次方程备课课件ppt: 这是一份数学1 一元二次方程备课课件ppt,共17页。PPT课件主要包含了8-2x,5-2x,18m2,X+1,X+2,X+3,X+4,想一想,X+6,一个未知数X的等内容,欢迎下载使用。
数学八年级下册第九章 图形的相似5 相似三角形判定定理的证明图片ppt课件: 这是一份数学八年级下册第九章 图形的相似5 相似三角形判定定理的证明图片ppt课件,共28页。













