初中冀教版12.1 分式备课课件ppt

这是一份初中冀教版12.1 分式备课课件ppt，共28页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，分式约分的符号法则，想一想，－2x2＋3x－2，最简分式等内容，欢迎下载使用。

约分分式约分的符号法则最简分式分式的值
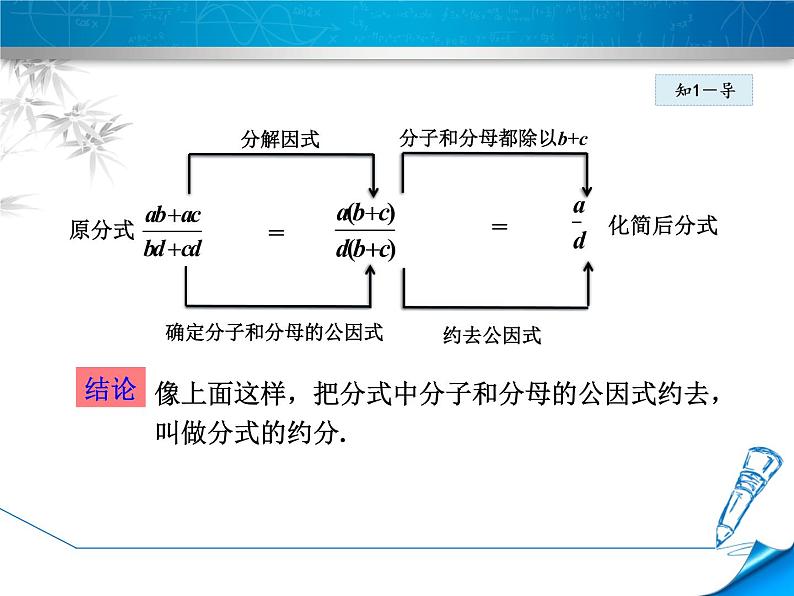
有若干张如图①所示的小长方形纸片，设它的面积为S，长为x，则它的宽为多少？用n张这样的小长方形纸片拼成如图②的长方形，它的长是nx，则它的宽可以怎样表示?由此你能写出哪些相等的分式？你发现了什么？
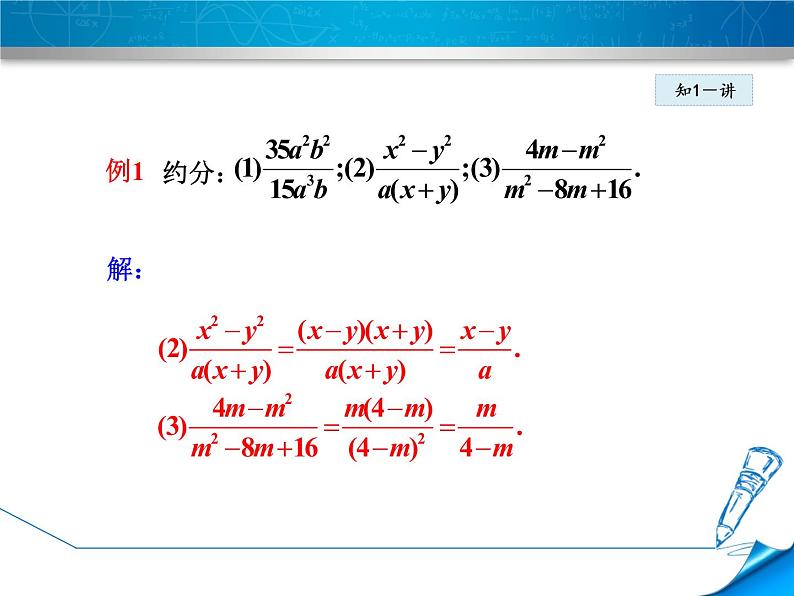
分式 能不能化简？如果能，那么化简的依据是什么，化简的结果又是什么？ 分式 可以化简，化简过程为：
像上面这样，把分式中分子和分母的公因式约去，叫做分式的约分.
分子和分母都除以b+c
确定分子和分母的公因式
约分的方法： 分式的分子、分母同除以它们的公因式． (1)约分的关键是找出分子、分母的公因式． (2)找公因式的方法：①当分子、分母是单项式时，先找分子、分母系数的最大公约数，再找相同字母的最低次幂，它们的积就是公因式；②当分子、分母是多项式时，先把多项式分解因式，再按①中的方法找公因式．
(3)分子、分母都是单项式的分式的约分应约去分子、 分母中相同字母(或含有字母的式子)的最低次幂，并约去 系数的最大公约数． (4)分子、分母都是多项式的分式的约分应先把分子、 分母分解因式，将其转化为因式乘积的形式，然后进行 约分． (5)约分后的结果是最简分式或整式． (6)约分的依据是分式的基本性质中的 (其中M是不等于0的整式)．
当分式的分子、分母是单项式时，约去分子、分母中相同字母(或含有字母的式子)的最低次幂，并约去系数的最大公约数．
2 已知 ，则分子与分母的公因式是(　　) A．4ab　 B．2ab 　C．4a2b2　　D．2a2b23 【中考·台州】化简 的结果是(　　) A．－1 B．1 C. D.
下列等式成立吗？为什么？
分式的符号准则：将分式、分子、分母的符号改变其中的任意两个，其结果不变．即：
例2 不改变分式 的值，使分子、分母的第 一项系数不含“－”号．
错解：错解分析：上述解法出错的原因是把分子、分母的第 一项的符号当成了分子、分母的符号．正确解法：
当分式的分子、分母是多项式时，若分子、分母的第一项的系数是负数，应先提取“－”号并添加括号，再利用分式的基本性质化成题目要求的结果；变形时要注意不要把分子、分母的第一项的符号误认为是分子、分母的符号．
1 填上分母，使等式成立：2 下列分式： 其中与 相等的是(　　) A．(1)(2) B．(3)(4) C．(2)(3) D．(1)(2)(3)(4)
3 下列变形正确的是( ) A． B． C． D．
分子和分母没有公因式的分式叫做最简分式. 如在分式 中，分子和分母的公因式为b+c，约去这个公因式，得到 ，分式 是最简分式. 约分是为了将分式化为最简分式.
最简分式的条件： (1)分子、分母必须是整式； (2)分子、分母没有公因式．
例3 下列各式中，最简分式有(　　) A．1个　　B．2个　　C．3个　　D．4个
导引：本题考查最简分式的概念．m＋n与m2－n2有 公因式m＋n，所以 ；x2－2xy ＋y2＝(x－y)2，故 .因此， 最简分式有
判定最简分式的唯一标准是分式的分子与分母没有公因式．
1 【中考·滨州】下列分式中，最简分式是(　　) A. B. C. D.下列各式中，是最简分式的是________．(填序号) ① ② ③ ④ ⑤
3 下列分式中，是最简分式的有( )
A．1个 B．2个 C．3个 D．4个
当p=12，q=－8时，请分别用直接代入求值和化简后代入求值两种方法求分式 的值，并比较哪种方法较简单.
例4 已知 ，求分式 的值.
导引： 由条件可知 y≠0，因此y2≠0.根据分式的基本性质， 将分式的分子和分母同时除以y2转化为含有 的式 子，再将条件代入即可求值．解：由条件可知y≠0，因此y2≠0. 原式
本题运用了整体思想求值．关键是将所求分式利用分式的基本性质化出含有条件中的式子，再将条件式子整体代入求值．本例也可以将y看作已知量，把x＝ y代入所求分式求值．
已知 (其中x≠0)，求分式 的值．
2 当x＝－5时，分式 的值为(　　) A. B． C. D． 3 【中考·东营】若 ，则 的值为(　　) A．1 B. C. D.