初中数学冀教版八年级下册22.4 矩形公开课课件ppt

这是一份初中数学冀教版八年级下册22.4 矩形公开课课件ppt，共17页。PPT课件主要包含了问题思考，矩形的判定二，课堂小结，EBDC，不合格，对角线互相垂直等内容，欢迎下载使用。

门窗、方砖、数学教科书等都是什么图形?
一天,小丽和小娟到一个商店准备给今天要过生日的小华买生日礼物,选了半天,她们俩最后决定买相框送给小华,在里面摆放她们三个人的相片,为了相框摆放的美观性,她们选择了矩形的相框,那么她们是用什么方法知道拿的就是矩形相框呢?
活动1　矩形的判定(一)
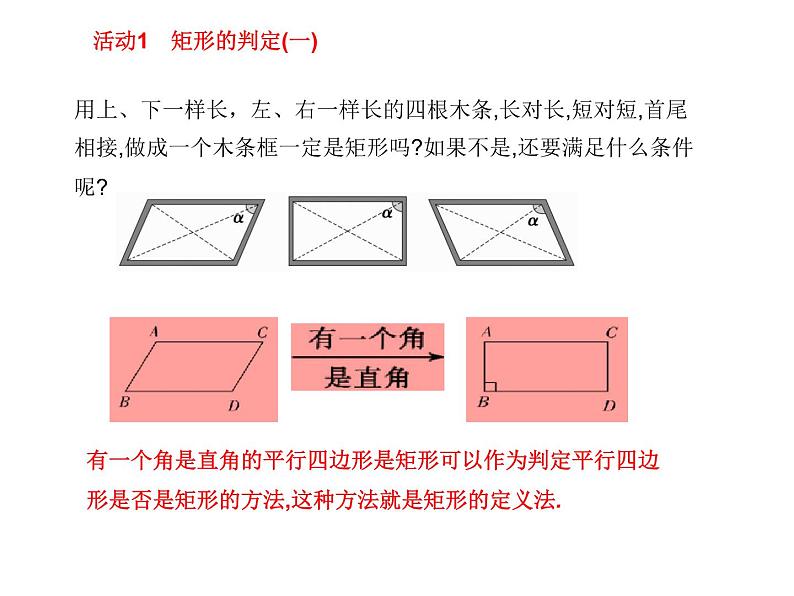
用上、下一样长，左、右一样长的四根木条,长对长,短对短,首尾相接,做成一个木条框一定是矩形吗?如果不是,还要满足什么条件呢?
有一个角是直角的平行四边形是矩形可以作为判定平行四边形是否是矩形的方法,这种方法就是矩形的定义法.
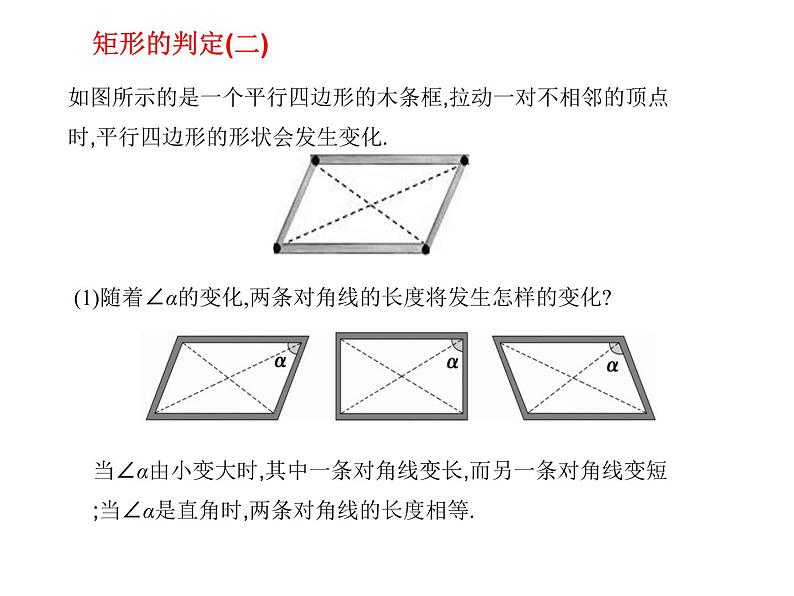
如图所示的是一个平行四边形的木条框,拉动一对不相邻的顶点时,平行四边形的形状会发生变化.
(1)随着∠α的变化,两条对角线的长度将发生怎样的变化?
当∠α由小变大时,其中一条对角线变长,而另一条对角线变短;当∠α是直角时,两条对角线的长度相等.
(2)当两条对角线的长度相等时,平行四边形有什么特征?由此你能得到一个怎样的猜想?
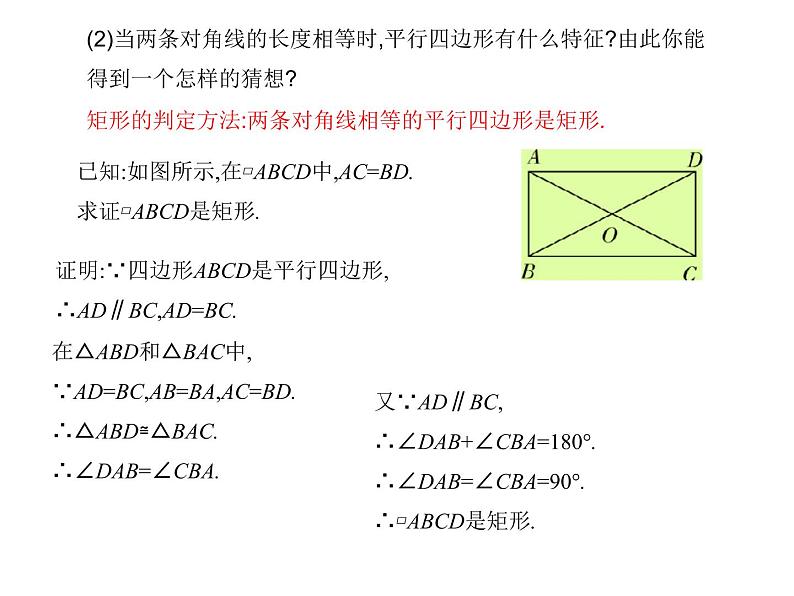
矩形的判定方法:两条对角线相等的平行四边形是矩形.
已知:如图所示,在▱ABCD中,AC=BD.求证▱ABCD是矩形.
证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.
在△ABD和△BAC中,∵AD=BC,AB=BA,AC=BD.∴△ABD≌△BAC.∴∠DAB=∠CBA.
又∵AD∥BC,∴∠DAB+∠CBA=180°.∴∠DAB=∠CBA=90°.∴▱ABCD是矩形.
活动3　矩形的判定(三)
想一想:矩形的四个角是直角,反过来,一个四边形至少有几个角是直角时,这个四边形就是矩形呢?
结论:“有三个角是直角的四边形是矩形”.
[知识拓展]　(1)由四边形直接判定矩形的方法是:有三个角是直角的四边形是矩形.(2)由平行四边形判定矩形的方法有:　①有一个角是直角的平行四边形是矩形.　②对角线相等的平行四边形是矩形.
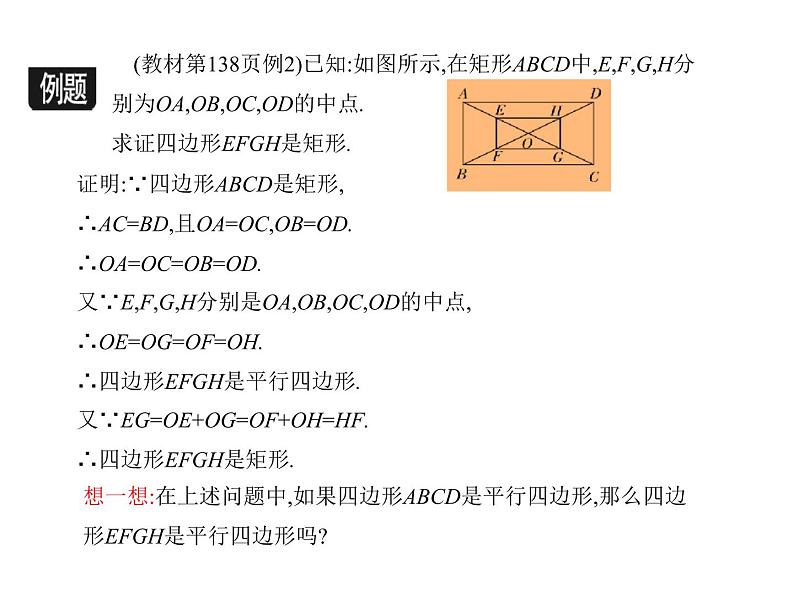
　(教材第138页例2)已知:如图所示,在矩形ABCD中,E,F,G,H分别为OA,OB,OC,OD的中点.求证四边形EFGH是矩形.
证明:∵四边形ABCD是矩形,∴AC=BD,且OA=OC,OB=OD.∴OA=OC=OB=OD.
又∵E,F,G,H分别是OA,OB,OC,OD的中点,∴OE=OG=OF=OH.∴四边形EFGH是平行四边形.
又∵EG=OE+OG=OF+OH=HF.∴四边形EFGH是矩形.
想一想:在上述问题中,如果四边形ABCD是平行四边形,那么四边形EFGH是平行四边形吗?
1.矩形的判定方法:(1)有一个角是直角的平行四边形是矩形.(2)有三个角是直角的四边形是矩形.(3)对角线相等的平行四边形是矩形.
2.判定一个四边形是矩形的方法与思路是:
1.如图所示,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是(　　)A.AB=BE B.DE⊥DCC.∠ADB=90°D.CE⊥DE
解析:∵四边形ABCD为平行四边形,∴AD∥BC,且AD=BC.又∵AD=DE,∴DE=BC,∴四边形BCED为平行四边形.选项A,∵AB=BE,DE=AD,∴BD⊥AE,∴▱DBCE为矩形;选项B,∵DE⊥DC,∴∠EDB=90°+∠CDB>90°,∴四边形DBCE不能为矩形;选项C,∵∠ADB=90°,∴∠EDB=90°,∴▱DBCE为矩形;选项D,∵CE⊥DE,∴∠CED=90°,∴▱DBCE为矩形.故选B.
2.(2016·黑龙江中考)如图所示,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB.请你添加一个条件为　　　　,使四边形DBCE是矩形. 
解析:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴DE∥BC,又∵DE=AD,∴DE=BC,∴四边形DBCE为平行四边形.又∵EB=DC,∴四边形DBCE是矩形.故填EB=DC.
3.木工师傅做了一张桌面,要求为矩形,现量得桌面的长为60 cm,宽为32 cm,对角线长为66 cm,这个桌面　　　　(填“合格”或“不合格”). 
解析:根据勾股定理求出桌面的对角线长为68 cm.故填不合格.
4.如图所示,E,F,G,H分别是四边形ABCD四条边的中点,要使四边形EFGH为矩形,四边形ABCD应具备的条件是　 　　　 . 
解析:连接BD,AC.∵H,G分别是AD,CD的中点,∴HG是△DAC的中位线,∴HG∥AC,同理可得EF∥AC,HE∥BD∥FG.∵四边形EHGF是矩形,∴∠FEH=∠EHG=∠HGF=∠EFG=90°,∴DB⊥AC.故填对角线互相垂直.
5.在△ABC中,D是BC边的中点,E,F分别在AD及其延长线上,CE∥BF,连接BE,CF.(1)求证△BDF≌△CDE;
(2)若DE= BC,试判断四边形BFCE是怎样的四边形?并证明你的结论.
解析:(1)由CE∥BF得出∠CED=∠BFD,根据“AAS”推出△BDF≌△CDE;(2)根据三角形全等得出DE=DF,根据BD=DC推出四边形BFCE是平行四边形,求出∠BEC=90°,根据矩形的判定定理即可推得结论.
证明:(1)∵CE∥BF,∴∠CED=∠BFD.∵D是BC边的中点,∴BD=DC.在△BDF和△CDE中,
∴△BDF≌△CDE(AAS).
解:(2)四边形BFCE是矩形.证明:∵△BDF≌△CDE,∴DE=DF.∵BD=DC,∴四边形BFCE是平行四边形.∵BD=CD,DE= BC,∴BD=DC=DE,∴∠BEC=90°,∴平行四边形BFCE是矩形.
6.如图所示,在△ABC中,AB=AC,D为BC边的中点,以AB,BD为邻边作▱ABDE,连接AD,EC.求证四边形ADCE是矩形.
解析:由等腰三角形“三线合一”的性质得出AD⊥BC,BD=CD,∠ADC=90°,从而由平行四边形的性质得出AE∥BD,AE=BD,从而得出AE∥CD,AE=CD,证出四边形ADCE是平行四边形,即可得出结论.
证明:∵AB=AC,D为BC边的中点,∴AD⊥BC,BD=CD,∴∠ADC=90°.∵四边形ABDE是平行四边形,∴AE∥BD,AE=BD,∴AE∥CD,AE=CD,∴四边形ADCE是平行四边形.又∵∠ADC=90°,∴四边形ADCE是矩形.
7.如图所示,在△ABC中,O是边AC上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交△BCA的外角平分线于点F.
(1)求证OE=OF;(2)当点O运动到何处时,四边形AECF是矩形?
解析:(1)根据MN∥BC,CE平分∠ACB,CF平分∠ACD,得到相等的角,再由等角对等边即可证得OE=OF;(2)根据矩形的性质可知矩形的对角线互相平分,即AO=CO,OE=OF,故当点O运动到AC的中点时,四边形AECF是矩形.
证明:(1)∵MN∥BC,∴∠OEC=∠ECB.∵CE平分∠ACB,∴∠BCE=∠ACE,∴∠OEC=∠ACE.∴OE=OC.同理可证OC=OF.∴OE=OF.
解:(2)当点O运动到AC的中点时,四边形AECF是矩形.理由如下:∵AO=CO,OE=OF,∴四边形AECF是平行四边形.∵∠ECA+∠ACF= ∠ACB+ ∠ACD,∴∠ECF=90°,∴四边形AECF是矩形.
8.如图所示,BD是▱ABCD的对角线,E,F分别为BD上两点,AC交BD于点O. (1)请你添加一个条件,使得△ABE≌△CDF,并证明;(2)在问题(1)中,当AC与EF满足什么条件时,四边形AECF是矩形,请说明理由.
解析:(1)根据平行四边形的性质得一组边相等、一组角相等,然后找到另外一组相等的角或相等的边即可证明全等;(2)首先得到四边形AECF是平行四边形,然后利用对角线相等的平行四边形是矩形即可判定.
解:(1)(答案不唯一)添加条件BE=DF即可证得△ABE≌△CDF.证明如下:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB.在△ABE和△CDF中,∴△ABE≌△CDF.
(2)当AC=EF时,四边形AECF是矩形.理由如下:∵四边形ABCD是平行四边形,∴∠BAC=∠DCA.由△ABE≌△CDF知∠BAE=∠DCF,AE=CF,∴∠EAO=∠FCO,∴AE∥CF.∴四边形AECF是平行四边形.∵AC=EF,∴四边形AECF是矩形.