初中2 幂的乘方与积的乘方精品课件ppt

这是一份初中2 幂的乘方与积的乘方精品课件ppt，共17页。PPT课件主要包含了学习目标，复习导入，x10，am+n，amn，底数不变，指数相乘，指数相加，amnamn，am·anam+n等内容，欢迎下载使用。
1.理解并掌握积的乘方的运算法则；（重点）2.掌握积的乘方的推导过程，并能灵活运用.（难点）
1.计算: （1） 10×102× 103 =______ ； （2） (x5 )2=_________.
2.（1）同底数幂的乘法：am·an= ( m，n都是 正整数).
（2）幂的乘方：(am)n= (m,n都是正整数）.
其中m , n都是正整数
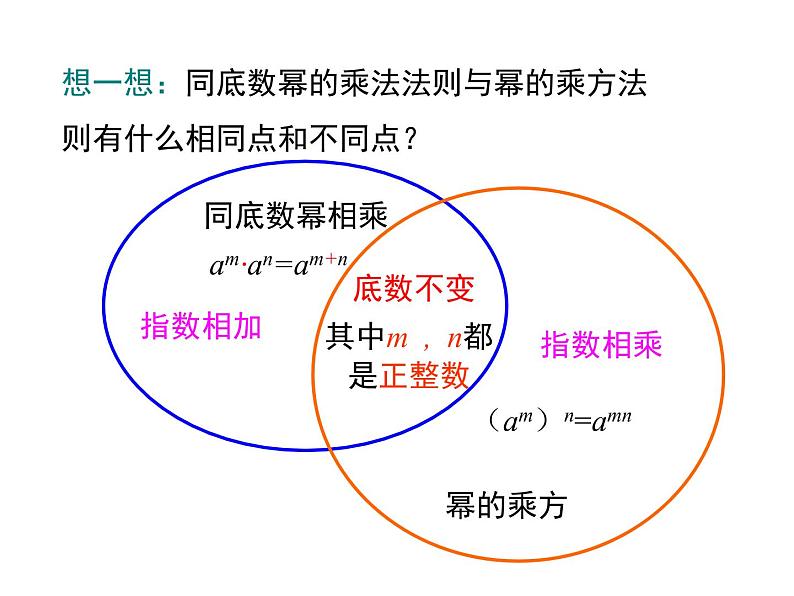
想一想：同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点？
我们学过的幂的乘方的运算性质适用吗？
我们只能根据乘方的意义及乘法交换律、结合律可以进行运算.
底数为两个因式相乘，积的形式.
（乘法交换律、结合律）
（同底数幂相乘的法则）
思考：积的乘方(ab)n =?
因此可得：(ab)n=anbn (n为正整数).
(ab)n=anbn (n为正整数)
积的乘方法则:积的乘方,等于把积的每一个因式分别乘方，再把所得的幂相乘.
(ab)n = anbn （n为正整数）
想一想：三个或三个以上的积的乘方等于什么？
(abc)n = anbncn （n为正整数）
例1 计算: (1)(3x)2 ； (2)(－2b)5 ； (3)(－2xy)4 ； (4)(3a2)n.
例2 太阳可以近似地看作是球体，如果用V、R 分别代表球的体积和半径，那么V＝ πR3，太阳的半径约为6×105千米，它的体积大约是多少立方千米(π取3)?
解：∵R＝6×105千米，∴V＝ πR3 ≈ ×3×(6×105)3≈8.64×1017(立方千米)．答：它的体积大约是8.64×1017立方千米．
逆用幂的乘方的运算性质
逆用同底数幂的乘法运算性质
逆用积的乘方的运算性质
提示：可利用 简化运算
幂的运算法则的反向应用
an·bn = (ab)n
am+n =am·an
(1)（ab2)3=ab6 ( )
(2) (3xy)3=9x3y3 ( )
(3) (－2a2)2=－4a4 ( )
(4) －(－ab2)2=a2b4 ( )
1.判断:
2.下列运算正确的是（ ） B.(xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
3. (0.04)2018×[(－5)2018]2=________.
(1) (ab)8; (2) (2m)3; (3) (－xy)5; (4) (5ab2)3; (5) (2×102)2; (6) (－3×103)3.
解：(1)原式=a8·b8;
(2)原式= 23 ·m3=8m3;
(3)原式=(－x)5 ·y5=－x5y5;
(4)原式=53 ·a3 ·(b2)3=125a3b6;
(5)原式=22 ×(102)2=4 ×104;
(6)原式=(－3)3 ×(103)3=－27 ×109=－2.7 ×1010.
（1）2(x3)2·x3－(3x3)3+(5x)2·x7; （2）(3xy2)2+(－4xy3) · (－xy) ; （3）(－2x3)3·(x2)2.
解：原式=2x6·x3－27x9+25x2·x7 = 2x9－27x9+25x9 = 0;
解：原式=9x2y4 +4x2y4 =13x2y4;
解：原式= －8x9·x4 =－8x13.
能力提升：如果(an.bm.b)3=a9b15,求m, n的值.
(an)3.(bm)3.b3=a9b15,
 a3n.b3m+3=a9b15,
 3n=9,3m+3=15.
解:∵(an.bm.b)3=a9b15,