冀教版22.6 正方形精品课件ppt

这是一份冀教版22.6 正方形精品课件ppt，共27页。PPT课件主要包含了问题思考，一组邻边分别相等，两组对边分别平行，相等且互相平分，轴对称图形，有一个直角，一组邻边相等，平行四边形，正方形，三个角是直角等内容，欢迎下载使用。

观察图片,回答下列问题:
1.上述图片中的四边形都是特殊的平行四边形,除菱形、矩形外,还有一种特殊的平行四边形,观察这些特殊的平行四边形,你能发现它们有什么共同特征吗?与同伴交流.
四个角都相等都是90°
2.观察特征,填写下表:
3.这种特殊的平行四边形与我们学过的菱形、矩形以及平行四边形之间有什么联系与区别?如何给出这个定义?
正方形的定义:有一组邻边相等,且有一个角是直角的平行四边形叫做正方形.
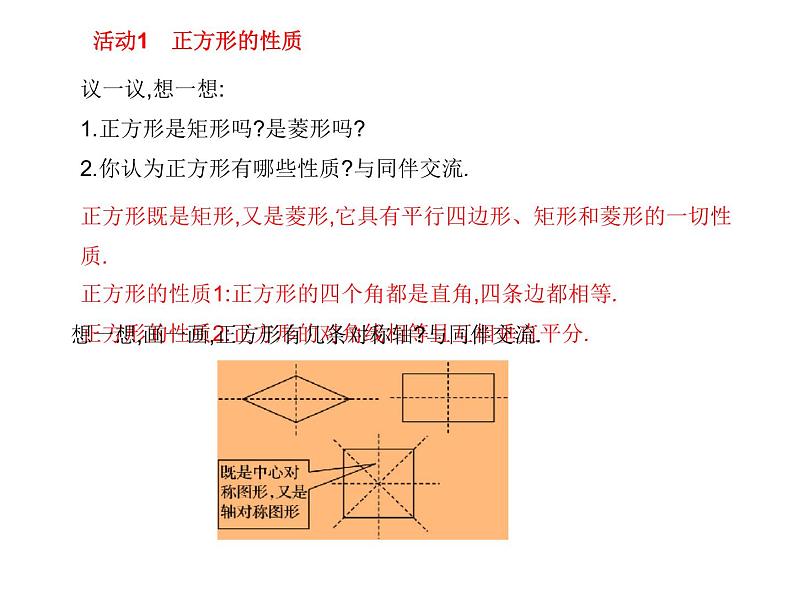
议一议,想一想:1.正方形是矩形吗?是菱形吗?2.你认为正方形有哪些性质?与同伴交流.
正方形既是矩形,又是菱形,它具有平行四边形、矩形和菱形的一切性质.正方形的性质1:正方形的四个角都是直角,四条边都相等.正方形的性质2:正方形的对角线相等且互相垂直平分.
想一想,画一画,正方形有几条对称轴?与同伴交流.
活动2　正方形的性质的运用
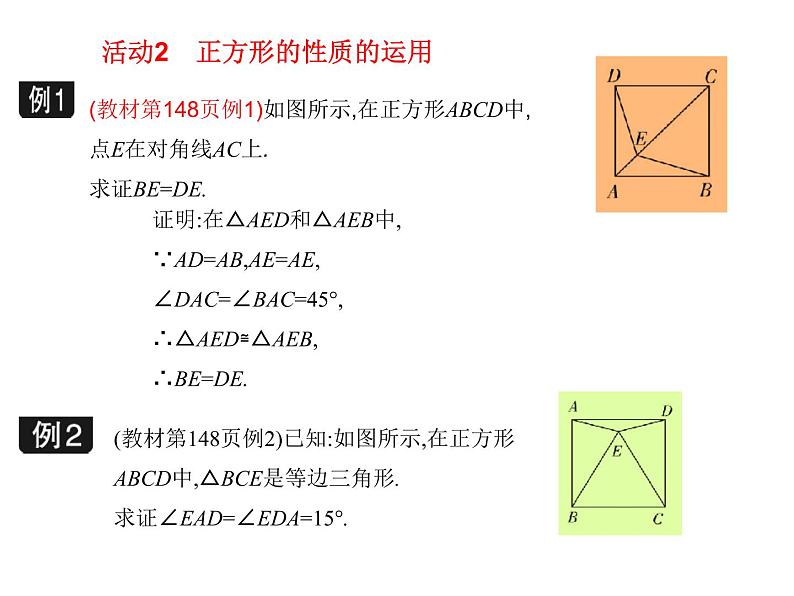
(教材第148页例1)如图所示,在正方形ABCD中,点E在对角线AC上.求证BE=DE.
证明:在△AED和△AEB中,∵AD=AB,AE=AE,∠DAC=∠BAC=45°,∴△AED≌△AEB,∴BE=DE.
(教材第148页例2)已知:如图所示,在正方形ABCD中,△BCE是等边三角形.求证∠EAD=∠EDA=15°.
平行四边形、矩形、菱形与正方形关系演示
正方形是特殊的平行四边形，也是特殊的矩形，也是特殊的菱形。
平行四边形、矩形、菱形、正方形的关系
活动4　正方形的判定定理
(1)对角线相等的菱形是正方形.
(4)有一组邻边相等的矩形是正方形.
(3)有一个角是直角的菱形是正方形.
(2)对角线垂直的矩形是正方形.
已知:如图所示,点E,F,M,N分别在正方形ABCD的四条边上,且AE=BF=CM=DN.求证四边形EFMN是正方形.
提示:先证明△AEN≌△BFE,得到NE=EF,∠AEN=∠BFE,∠ANE=∠BEF;再证明EF=FM,FM=MN,MN=NE,从而得到四边形EFMN是菱形,最后证明四边形EFMN是正方形.
已知:如图所示,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证四边形BECF是正方形.
分析:方法1:要证四边形BECF是正方形,可以先证明四边形BECF是菱形,然后证明四边形BECF中有一个角是直角即可;方法2:要证四边形BECF是正方形,可以先证明四边形BECF是矩形,然后证明四边形BECF中有一组邻边相等即可.
证法1:∵BF∥CE,CF∥BE,∴四边形BECF是平行四边形.∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°.∵BE平分∠ABC,CE平分∠DCB,∴∠EBC= ∠ABC=45°,∠ECB= ∠DCB=45°.∴∠EBC=∠ECB=45°.∴EB=EC.∴四边形BECF是菱形.在△EBC中,∠EBC=∠ECB=45°,∴∠BEC=90°.∴菱形BECF是正方形.
证法2:∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°.∵BE平分∠ABC,CE平分∠DCB,∴∠EBC= ∠ABC=45°,∠ECB= ∠DCB=45°,∴∠EBC=∠ECB=45°,∴EB=EC.∵BF∥CE,CF∥BE,∴∠ECB=∠CBF,∠EBC=∠FCB=45°,∴∠EBF=∠ECF=∠BEC=90°.∴四边形BECF是矩形.∴矩形BECF是正方形.
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
1.判断下列说法是否正确(1)有一个角为直角的菱形是正方形;(　　)(2)四个角都相等的四边形是正方形.(　　)(3)四条边都相等的四边形是正方形;(　　)(4)有一组邻边相等的矩形是正方形;(　　) (5)对角线垂直且相等的四边形是正方形;(　　)(6)对角线相等的菱形是正方形;(　　)(7)对角线互相垂直的矩形是正方形;(　　)(8)对角线互相垂直平分的四边形是正方形.(　　)
解析:直接根据正方形的判定方法逐一进行判定.
2.(2016·毕节中考)如图所示,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是(　　)　　A.3 B.4C.5D.6
解析:设CH=x,则DH=EH=9-x.∵BE∶EC=2∶1,∴CE= BC=3.∴在Rt△ECH中,EH2=EC2+CH2,即(9-x)2=32+x2,解得x=4,即CH=4.故选B.
3.(2016·台湾中考)如图所示,有一个平行四边形ABCD与一正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数为 (　　)A.50B.55C.70D.75
解析:∵四边形CEFG是正方形,∴∠CEF=90°.∵∠CED=180°-∠AEF-∠CEF=180°-15°-90°=75°,∴∠D=180°-∠CED-∠ECD=180°-75°-35°=70°.∵四边形ABCD为平行四边形,∴∠B=∠D=70°.故选C.
4.如图所示的是由四个全等的直角三角形拼成的“赵爽弦图”.在Rt△ABF中,∠AFB=90°,BF=3,AB=5.四边形EFGH的面积是　　　　. 
解析:因为AB=5,所以 =5×5=25.Rt△ABF中,BF=3,AB=5,则AF= =4,所以SRt△ABF= ×3×4=6,四个直角三角形的面积为:6×4=24.∴四边形EFGH的面积是25-24=1.故填1.
5.正方形的四条边　　　　 ,四个角　　　　 ,两条对角线　　　　 . 
解析:根据正方形的边、角、对角线的性质填空.
6.如图所示,过正方形ABCD的顶点B作直线l,过点A,C作l的垂线,垂足分别为E,F.若AE=1,CF=3,则AB的长度为　　　　. 
解析:∵四边形ABCD是正方形,∴∠CBF+∠FBA=90°,∠CBF+∠BCF=90°,∴∠BCF=∠ABE.∵∠AEB=∠BFC=90°,AB=BC,∴△ABE≌△BCF(ASA),∴AE=BF,BE=CF,∴AB= .故填 .
7.已知:如图所示,四边形ABCD为正方形,E,F分别为CD,CB延长线上的点,且DE=BF.求证∠AFE=∠AEF.
提示:可证△ABF≌△ADE,得到AF=AE.根据等边对等角证得∠AFE=∠AEF.