数学冀教版21.2 一次函数的图像和性质优秀课件ppt

这是一份数学冀教版21.2 一次函数的图像和性质优秀课件ppt，共30页。PPT课件主要包含了学习目标，一次函数的性质2等内容，欢迎下载使用。

1.经历作图过程，初步了解作函数图像的一般步骤；2.理解一次函数的代数表达式与图像之间的对应关系；3.能较熟练作出一次函数的图像.
已知函数的表达式，通过列表、描点和连线，可以在直角坐标系中画出这个函数图像。
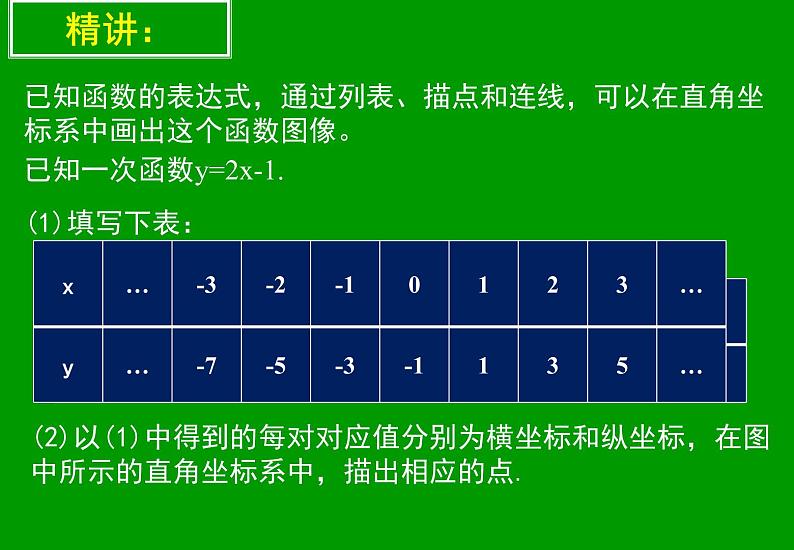
已知一次函数y=2x-1.(1)填写下表：
(2)以(1)中得到的每对对应值分别为横坐标和纵坐标，在图中所示的直角坐标系中，描出相应的点.
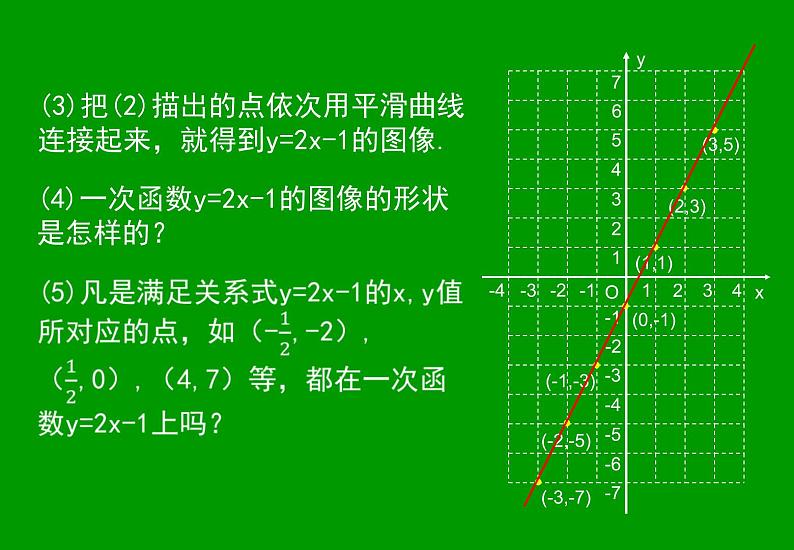
(3)把(2)描出的点依次用平滑曲线连接起来，就得到y=2x-1的图像.
(4)一次函数y=2x-1的图像的形状是怎样的？
一般地，一次函数y=kx+b的图像为一条直线.因此，我们把一次函数y=kx+b的图像也称为直线y=kx+b.在画一次函数的图像时，只要确定出两个点，再过这两点画直线就可以了.
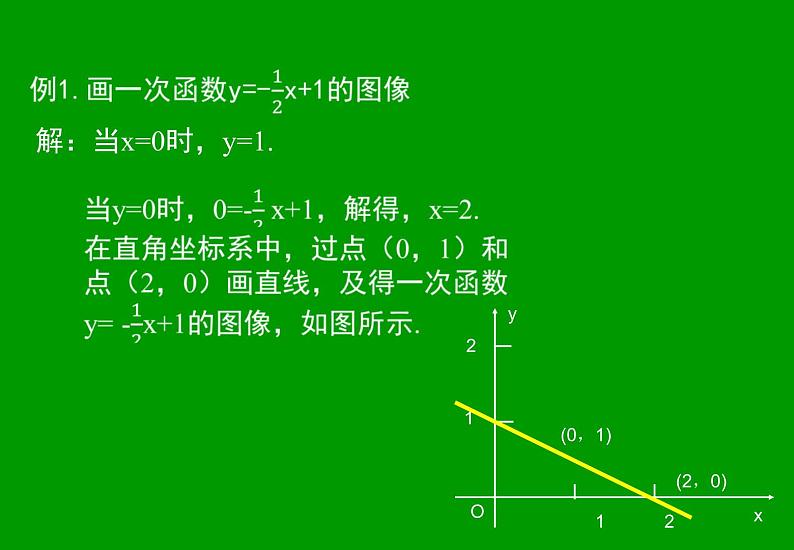
解：当x=0时，y=1.
在同一直角坐标系中，画出y=x和y=1-x的图像.
解析: 当x=0时，函数y=x=0；函数y=1-x=1. 当x=1时，函数y=x=1；函数y=1-x=0. 所以在坐标系中，过点(0，0)，(1，1)做直线，即可得一次函数y=x的图像；过点(0，1)，(1，0)做直线，即可得一次函数y=1-x的图像，如图：
观察 比较两个函数的相同点与不同点.
两图象都是经过原点的
正比例函数y= kx (k≠0) 的图象是经过原点(0,0)和点(1,k)的一条直线。
1. 填表并观察下列两个函数的变化情况.
(1)在同一个直角坐标系中画出这两个函数的图像.
(2)它们的图像有公共点吗？如果有，请写出公共点的坐标.
解析:(1) y=-5x+2的函数图像经过点(0，2)，(1，-3)，过这两点做直线，即为y=-5x+2的函数图像；y=x-10的函数图像经过点(0，-10),(2，-8)，过这两点做直线，即为y=-5x+2的函数图像.
(2)由图可知，这两个函数图像有公共点，由表可知，其公共点坐标为(2，-8)(或者联立这两个函数，令-5x+2=x-10，解得x=2，y=x-10=-8).
2. 今有一根弹簧，不悬挂重物时的长度为12cm，悬挂的重物每增加1kg(重物不超过8kg)，弹簧的长度就增加0.5cm.写出弹簧长度y(cm)和悬挂物的质量x(kg)之间的函数关系式，指出自变量的取值范围，并画出这个函数的图像.
自变量x的取值范围为：0≤x≤8.函数图像如图：
哪些函数，y的值是随x的值的增大而增大的？哪些函数，y的值是随x的值的增大而减小的？y的值随x的增大而增大和y的值随x值的增大而减小两种函数，它们的区别和自变量系数的符号有怎样的关系？
对于一次函数y=kx+b（k,b为常数，且k≠0）：当k>0时，y的值随x的值的增大而增大；当k<0时，y的值随x的值的增大而减小.
哪些函数的图像与y轴的交点在x轴的上方，哪些函数与y轴的交点在x轴的下方？函数的图像与y轴的交点在x轴的上方和函数的图像与y轴的交点在x轴的下方，这两种函数，它们的区别与常数项有怎样的关系？正比例函数的图像一定经过哪个点？
事实上，一次函数y=kx+b的图像是经过y轴上的点(0，b)的一条直线.当b＞0时，点(0，b)在x轴的上方；当b＜0时，点(0，b)在x轴的下方；当b=0时，点(0，0)是原点，即正比例函数y=kx的图像是经过原点的一条直线.
例1.已知关于x的一次函数y=(2k-1)x+(2k+1).(1)当k满足什么条件时，函数y的值随x的值的增大而增大？(2)当k满足什么条件时，y=(2k-1)x+(2k+1)的图像经过原点？(3)当k满足什么条件时，函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的下方？(4)当k满足什么条件时，函数y的值随x的值的增大而减小且函数图像与y轴的交点在x轴的上方？
解析: (1)当2k-1＞0时，y的值随x的值增大而增大. 解2k-1＞0，得：k＞0.5.(2)当2k+1=0，即k=-0.5时，函数y=(2k-1)x+(2k+1)的图像经过原点.(3)当2k+1＜0，函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的下方. 解2k+1＜0，得k＜-0.5.(4)当2k-1＜0时，y的值随x的值增大而减小.解得：k ＜0.5. 当2k+1＞ 0，函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的上方.解得k＞ -0.5. 所以此时k的取值范围为(-0.5，0.5).
1.判断下列函数中，y的值随x的值增大而变化的情况.
(1) y=-3x+3； (2) y=3x-3； (3) y=(3-π)x； (4) y=0.5x.
解析:(1)式中，-3＜0，所以该函数y的值随x的值增大而减小；(2)式中，3＞0，所以该函数y的值随x的值增大而增大；(3)式中，3-π＜0，所以该函数y的值随x的值增大而减小；(4)式中，0.5＞0，所以该函数y的值随x的值增大而增大.
2.已知关于x的一次函数y=kx+4k-2.(1)如果函数的图像经过原点，求k的值.(2)如果y的值随x的值的增大而减小，求k的取值范围.
解析:(1)该函数的图像经过原点，即其常数项为0，所以4k-2=0，解得，k=0.5.(2)该函数y的值随x的值的增大而减小，即其自变量系数小于0，所以k＜0.
3. 画出函数y=-3x+3的图像，结合图像回答下列问题：(1) y的值随x的值增大而 （填“增大”或“减小”），图像从左到右 （填“上升”或“下降”）(2)当y＜0时，求x的取值范围.(3)当0＜x＜1时，求y的取值范围.
(1)由图像可以得出答案.
(2)由图可知，当y＜0时，x的取值范围为x＞1.
(3)由图可知，当0＜x＜1时，y的取值范围为0＜y＜3.
4.某面食加工部每周用10000元流动资金采购面粉及其他物品，其中购买面粉的质量在1500kg-2000kg之间，面粉的单价为3.6元/千克，用剩余款额y元购买其他物品.设购买面粉的质量为x kg.
(1)求y与x的函数关系式，并写出自变量的取值范围.
(2)画出该函数的图像.
(3)观察图像，写出购买其他物品的款额y的取值范围.
解析: (1)由题意可知，购买面粉的资金为3.6x，总资金为10000元，即3.6x+y=10000，所以该函数式为:y=-3.6x+10000，其中x的取值范围是1500≤x≤2000.
(2)该函数图像如图所示：
(3)观察图像，由图可知，该函数随x值的增大，y的值逐渐变小.所以y的值最大为y=-3.6x+10000=10000-(-3.6*1500)=4600；最小为y=-3.6x+10000=10000-(-3.6*2000)=2800.y的取值范围即为:2800≤y≤4600.
(2013 遵义）P1(x1，y1)，P2(x2，y2)是正比例函数y=-0.5x图象上的两点，下列判断中，正确的是( )
解析:根据正比例函数图象的性质: 当k＜0时，y随x的增大而减小，所以D为正确答案．
A. y1＞y2 C.当x1＜x2时，y1＜y2
B. y1＜y2 D.当x1＜x2时，y1＞y2
(2013 眉山）若实数a,b,c满足a+b+c=0，且a＜b＜c，则函数y=cx+a的可能是( )
解析:由于a+b+c=0，且a＜b＜c，所以a＜0＜c，因为c＞0，所以y的值随x的值的增大而增大; a＜0，所以该函数与y轴的交点在y轴负半轴.观察图象可知，C为正确答案.
A. B. C. D.
(2013 鞍山）在一次函数y=kx+2中，若y随x的增大而增大，则它的图象不经过第 象限．
解析:由于y随x的增大而增大，所以k＞0，同时2＞0，所以大致图象如下图所示，
故而该函数的图象经过一、二、三象限，不经过第四象限.
1.一次函数y=kx+b的图像为一条直线，故其图像又称为直线y=kx+b. 2.一次函数y=kx+b中的系数k与b决定着它的性质：(1)当k＞0时，y随x的增大而增大，图像从左向右是上升的.(2)当k＜0时，y随x的增大而减小，图像从左向右是下降的.(3)当b=0时，一次函数y=kx+b为正比例函数y=kx，它的图像一定经过原点.(4)当b≠0时，直线y=kx+b一定不经过原点.