冀教版八年级下册21.1 一次函数说课ppt课件

这是一份冀教版八年级下册21.1 一次函数说课ppt课件，共58页。PPT课件主要包含了一次函数，课程导入，练一练，一起探究，知识结构，注意事项等内容，欢迎下载使用。

在本章中，我们将学习一次函数一次函数的图象和性质一次函数的表达式及其确定方法一次函数与方程、不等式的关系一次函数的应用
我们已经知道函数是刻画变量之间关系的数学模型，这些模型有多种形态，其中最简单的一种就是一次函数。你知道什么样的函数叫做一次函数吗？一次函数有什么特点呢？不妨先来做做下面几道题吧！
1.长江三峡大坝从2003年6月1日开始下闸蓄水，到6月10日，水库的水位由106m升至135m。如果这段时间按220h计算，且将水位的上升看做匀速的，那么，水库的水位y(m)和下闸蓄水的时间t(h)之间的函数关系是怎样的呢？2.某新建住宅小区物业管理部门按房主的住房面积收取物业管理费，每月按 1.60元/平方米收取，对有汽车的房主每月再收取车库使用费80元。设有汽车房主的住房面积为x m2。每月应收房主物业管理费与车库使用费共为y元，请写出y与x的函数关系式：3.小刚家道学校的路程为3.5km。他每天骑自行车去上学，速度为0.2km/min。 (1)在上学的路上，小刚离开家的路程s1(km)与 离开家的时间t(min)的函数关系式为： （2）在上学的路上，小刚距学校的路程s2 (km)与 离开家的时间t(min)的函数关系式为：
s2=3.5-0.2×t
观察上面几个函数表达式，它们有什么共同热点呢？
它们都是用自变量的一次整式来表示的
如果两个变量x和y之间的函数关系式可以表示成y=kx+b(k,b为常数，k≠0的形式，那么就称y是x的一次函数。特别的，当b=0时，一次函数就成为y=kx(k为常数， k≠0）。这时y叫做x的正比例函数。
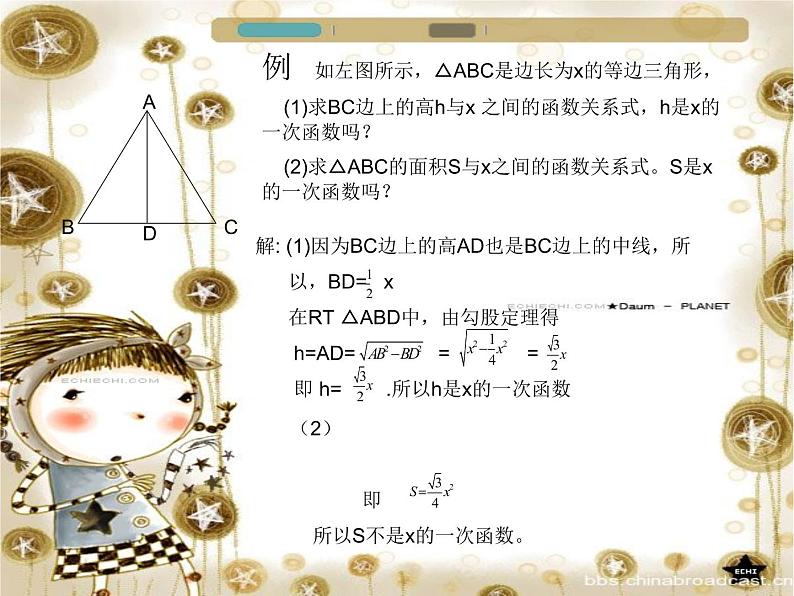
例 如左图所示，△ABC是边长为x的等边三角形， (1)求BC边上的高h与x 之间的函数关系式，h是x的一次函数吗？ (2)求△ABC的面积S与x之间的函数关系式。S是x的一次函数吗？
1. 在函数①y=2-x②y=8+0.03t③y=1+x+1/x④y=(x+3)/x中，是一次函数的有————2. 如果等腰三角形的周长是20 cm,底边是x cm,那么腰长y(cm)与底边长x(cm)之间的函数关系是什么？这个函数是一次函数吗？
y=(20-x)/2 它是一次函数
25.2 一次函数的图象和性质
一次函数是一种形式上比较简单的函数，相应地，它的图像和性质又有什么特点呢？ 我们已经知道，对于由表达式给出的函数，可以由表达式确定出两个变量的一系列对应的数值，在直角坐标系中，以这些对应值为坐标描出相应的点，再用平滑的线连结这些点，就可以得到这个函数的图像
已知一次函数y=2x-1(1)填写下表：(2)以(1)中得得到的每对对应值分别为横坐标和纵坐标，在下图的直角坐标系中描出相应的点。 (3)把由(2)得到的点依次连结起来，就得到了y=2x-1的图像。
1.一次函数y=2x-1图像的形状是怎样的？你和其他同学得到的结果是一样的吗？2.凡是满足关系式y=2x-1的x,y的值所对应的点(x,y)如(-1,-3),(1,1),(4,7)……都在一次函数y=2x-1的图像上吗？3.请你从一次函数y=2x-1的图像上任意取一点，检验该点的横坐标x纵坐标y是否满足关系式y=2x-1.
我们看到，一次函数y=kx+b的图像是一条直线。这样，在画一次函数的图像时，只要确定出两个点，再过这两点画直线就可以了。正式因为一次函数的图像时一条直线，所以也把一次函数y=kx+b的图像称为直线y=kx+b。
例 1.在同一直角坐标系中画出y=3x+2和y=-2x的图像。 2. 在同一直角坐标系中画出y=x和y=1-x的图像。
仔细观察上面的y=-2x和 y=x这两个正比例函数的图像，你会发现什么？怎样更画正比例函数的图像更简单？
事实上，正比例函数的图像是经过原点O(0,0)的一条直线。所以，在画正比例函数的图像时，只需再找到一个点，连结它和原点就可以得到正比例函数的图像。
我们已经画了几个一次函数的图像了，你有没有发现一次函数y=kx+b的性质呢？什么样的函数y的值随x的值增大而增大的？什么样的函数y的值随x的增大而减小的？这两类函数的区别和自变量的系数的符号有什么关系？
一次函数y=kx+b的性质
当k>0时，y的值随x的增大而增大当k<0时，y的值随x的增大而减小
一、已知两个函数：y1=2x+30,y2=4x。1.不画出它们的图像，说出当x的值增大时，y1，y2的值怎样变化。2.当x从1开始增大时，预测哪个函数的值先达到80.3.函数值增大的快慢与k（这里k>0）的值有什么关系？
二、如果一次函数y=(k+1)x-1的y的值随x的增大而减小，那么k的取值范围是————
确定一次函数表达式的方法
许多实际问题的解决都需要求出一次函数的表达式。那么怎样才能简便地求出一次函数的表达式呢？
如图所示，直线是一个一次函数的图像。已知这个图像（直线）上的两点坐标P（-20，5），Q（10，20），怎样确定这个一次函数的表达式呢？
设这个一次函数的表达式为 y=kx+b（1）因为点P,Q在在它的图像（直线）上，所以这个两点的坐标都应当满足表达式（1）。即： 5=-20k+b, 20=10k+b.解这个关于k和b的二元一次方程组，得 k=1/2, b=15.所以这个一次函数的表达式为 y=1/2x+15.
讨论一下，这样做对吗？请说明理由。
某汽车再加油后开始匀速行驶。知汽车行驶至20km时，油箱剩油58.4L；行驶至50km时，油箱剩油56L.如果油箱中剩余油量y(L)与汽车行驶的路程(km)之间的关系是一次函数关系，请你求出这个一次函数的表达式，并写出自变量的取值范围。
根据上题思想,做一做这道题吧
解:设方程为y=kx+b.已知过P(20,58.4),Q(50,56)两点,即: 58.4=20k+b 56=50k+b解得 b=60,k=-2/25则方程为 y=-2/25x+60当y=0时,x=750故自变量的取值范围为[0,750]
前面讲了两道题,都是在明显看到是一次函数的的情况下做的.那么,当不知道是一次函数时该怎么做呢?
一定质量的气体，在体积不变的情况下，压强随温度的变化而变化。下表是一定质量的某种气体在体积不变的情况下，其压强p（千帕）随温度t（。c）变化的试验数据：
1.由表格中的数据可以看出：0。c时的压强为100千帕，温度每升高1。c，压强增大2/5千帕。由此能写出p（千帕）与t（。c）之间的函数关系式吗？它是一次函数吗？ 2.如果设这个一次函数的表达式为p=kt+b，你能用解二元一次方程组的方法求出和吗？请你用这种方法把函数表达式求出来。
我们大家来探究一下吧!
1.由一次函数的表达式y=kx+b得,x每增加1,y增加k.表格中的数据符合该特点,故是一次函数.2.设表达式为p=kx+b,P(0,100),Q(5,102)在满足表达式则有100=b ,102=5k+ b 解得b=100, k=-2/5 .故表达式为p=-2/5x+100
求一次函数（含正比例函数）的表达式常有以下几种情况： 1.由问题的实际意义直接写出。 2.确认其为一次函数，然后采用以下步骤：（1）设表达式为y=kx+b(正比例函数设为y=kx)（2）根据变量的两组对应值（正比例函数只需要一组）列方程组（或方程），求出k与b的值。
1.一次函数的图像过点A（1，2）和点B（-2，1），则该函数的表达式为————。2.由S市寄往G市的包裹，邮寄费用的标准是3元每千克，每件另收挂号费2元。(1)写出邮寄总费用（元）与包裹质量（千克）之间的函数关系。（2）如果邮寄包裹的质量为7.8，那么，邮寄总费用是多少？
1. y=1/3x+5/3 解析:设函数的表达式为y=kx+b 过A（1，2）和点B（-2，1）则有2=k+b,1=-2k+b解得k=1/3, b=5/3.2. (1) y=3x+2 (2) 3*7.8+2=25.4
作业 第1题 第2题 第4题
第四节 一次函数与方程、不等式的关系
我们曾经学习过一元一次方程、一元一次不等式以及二元一次方程组，现在我们又学习了一次函数，你是否想过他们既然都是“一次”的，其中会不会有什么内在联系呢？
已知一次函数y=2x-1 (1)在如图的直角坐标系中，画出它的图像。（2）对这个一次函数，x取何值时，它所对应的y的值等于5？对这个一次函数，x取何值时，它所对应的y的值大于5？对这个一次函数，x取何值时，它所对应的y的值小于5？ (3）由图像上点的坐标，对（2）中各问题的结论作出解释。
分析 容易看出，对一次函数y=2x-1，求“x取何值时，它对应的的值等于5” ，就是求一元一次方程 2x-1=5的解；求“x取何值时，它对应的的值都大于（或小于）5“，就是求一元一次方程 2x-1>5（或2x-1<5)的解集。
由此看出，一次函数与一元一次方程、一元一次不等式有密切的联系!
例题： 已知函数y1=-2x+3和y2=1/2x-2.(1)x取何值时，y1=y2？(2)x取何值时，y1>y2？(3)x取何值时，y1解： （1）要使y1=y2，就时要使 -2x+3=1/2x-2. 解这个方程，得 x=2。 即当 x=2时，y1=y2 （2）要使y1>y2，就时要使 -2x+3>1/2x-2. 解这个方程，得 x<2。 即当 x=2时，y1>y2。 （3）要使y12。 即当 x=2时，y1由图像也可以看出：这个函数的图像的交点是（2，-1），也就是当x=2时，y1和y2的值相等，都等于-1；当x<2时，y1=-2x+3的图像在y2=1/2x-2的图像的上方，这说明此y1>y2；当x>2时，y1=-2x+3的图像在y2=1/2x-2的图像的下方，这说明此时y1 解一次不函数有两种方法。第一，用解一次不等式的方法来解；第二，先解一元一次方程，再利用图像分析。
借助一次函数的图像解方程组 x+y=7 3x-2y=6
答案： 借助图像可得： x=4，y=3
作业 第1题 第4题
一次函数在现实生活中有广泛的应用，现在我们就来就此尽心进行观察和探究。
模拟公司营销人员签订了这样的工作合同：工资由两部分组成，一部分是基本工资，每人每月300元；另一部分是按月销售量确定的工资，每销售一件产品奖励3元。
25.2 一次函数的应用
1.设某销售员每月销售x件商品，每月工资为y元,求x与y的关系式。2.用求出的函数关系式，尝试解决下列问题：（1）该营销员买月工资为1220元，他这个月销售了多收件产品？（2）要想使工资超过1500元，当月的销售量应为多少件？
事实上，营销员的月工资y（元）与他当月销售的件数x之间的函数关系式为： y=4x+300 当营销员的月工资为1220时，他的月销售产品受应该满足方程： 4x+300=1220 解这个方程得： x=230 要想每个月的工资超过1500元，当月的销售的产品数应当满足不等式： 4x+300〉1500 解这个不等式得： x〉300
某型号的体重秤，有效范围是0～100kg，称体重时，体重x(kg)与指针按顺时针方向转过的角度y（°）有如下一些对应数值：
1.请在直角坐标系中，分别以商标 中的每对对应数值为横坐标和纵坐标，描出相应的点，用线连接这些点，画出图象。 2.根据图像，求出x与y之间的函数关系，并写出自变量x的取值范围。 3.当体重为多少千克时，称的指针瞧好转了180°？
一个长方形的长，宽分别为60和40，现在他的款减少10，长增加x,设变化后长方形的面积为y。（1）写出x与y的函数关系式；（2）x取何值时，变化后的长方形与原来的长方形面积相等？（3）x去哪些值时，可以变化后的长方形的面积比原来的长方形的面积的2倍还大？
事实上，因为函数的图像是直线上的一段，并且经过原点，所以y是x的正比例函数，球的表达式为：y=18/5x 自变量的取值范围是：0<=x<=100 由180=18/5x，解得x=50，即称的体重为50千克，称的指针恰好转过了180°.
汽车在刹车后会由于惯性而继续向前弧形一段距离，这段距离脚刹车距离，某型号轿车的刹车距离 y（m）与轿车行驶的速度x（km/h）的关系如图所示。
（1）写出y与x之间的函数关系式。 （2）要刹车距离比超过4m，车速应但保持在那 个范围内？
25.1 一次函数25.2 一次函数的图像和 性质25.3 确定一次函数表达式的方法25.4 一次函数与方程、不等式的关系25.5 一次函数的应用
1.诸多函数中最简单的就是一次函数。 2.一次函数y=kx+b(k≠0)的图像是直线，所以又叫直线 y=kx+b。 3.一次函数y=kx+b(k≠0)中的k与b决定函数性质的基本矢 量： （1）当k＞0时，y随x增大而增大，其图像的趋势：从左 向右是上升的。 （2）当k＜0时，y随x增大而减小，其图像的趋势：从左向右是下降的。
（3）当b=0时，一次函数y=kx+b(k≠0)就变成y=kx (k≠0)，即正比例函数，它的图像过原点。 （4）当b≠0时，y=kx+b部过原点。 4.球一次函数的表达式至关重要，它是解决许多实际问题的关键环节。求一次函数的主要方法是： （1）有问题的实际意义直接写出，这种方法的实质是把问题中用文字叙述的数量关系用数学式子表达出来。 （2）根据图像、表格或已知条件确认（或近似看成）两个变量成一次函数，就可以将表达式设为y=kx+b，利用两组对应值求出k与b的值。这是一种重要的数学方法。
5.一次函数于一次方程及一次不等式有着密不可分的联系：（1）求函数y=kx+b与x轴交点的横坐标，只须另y=0，即解一次函数kx+b=0。（2）欲知x为何值时直线y=kx+b在轴的上方，只须另y＞0，即解一次不等式kx+b＞0。（3）求两直线y=kx+b与 y=kx+b的交点坐标，只须解一元二次方程组 y=kx+b y=kx+b（4）欲知x为何值时，直线y=kx+b在直线y=kx+b上方，只须另y=kx+b＞y=kx+b。
6.一次函数有着广泛的应用，掌握一次函数的应用有两个层次：（1）如果给出一次函数的表达式，则可直接用一次行数的性质解决问题。（2）如果问题只使用语言叙述或用表格或图片提供了一次函数的情境，则先求出表达式，仅‘而利用函数性质解决问题。
1.对于一次函数的概念，要把握函数表达式是一次式，而与表示自变量的字母无关。例如s=2t-5，y=3x+1等都是一次函数。2.在实际问题中，有时会遇到两个或多个一次函数图像拼接起来的图像。图1就是有两个一次函数图像组合‘而成的，对于其中的每一段，我们都可以用一次函数来分析。