初中冀教版第二十二章 四边形22.4 矩形授课ppt课件

这是一份初中冀教版第二十二章 四边形22.4 矩形授课ppt课件，共25页。PPT课件主要包含了平行四边形的性质，温故知新，一个角是直角，两组对边分别平行，情景创设，矩形的定义，变化过程，四个角都是直角，对边平行且相等，对角线互相平分且相等等内容，欢迎下载使用。

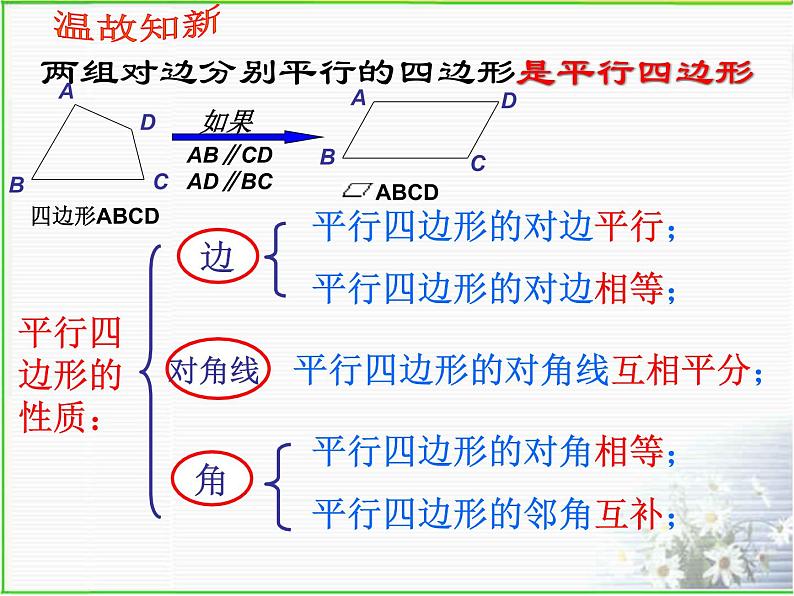
两组对边分别平行的四边形是平行四边形
平行四边形的对边平行；
平行四边形的对边相等；
平行四边形的对角相等；
平行四边形的邻角互补；
平行四边形的对角线互相平分；
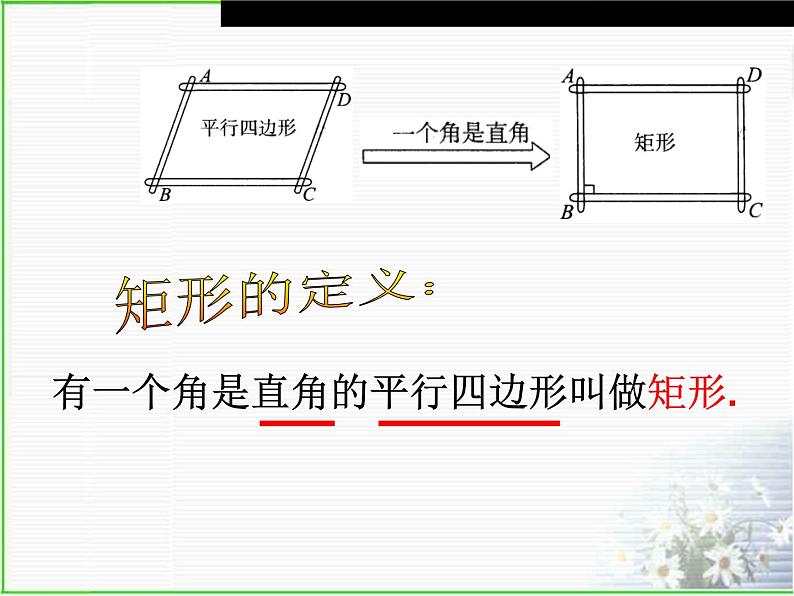
我们已经知道平行四边形是特殊的四边形，因此平行四边形除具有四边形的性质外，还有它的特殊性质，同样对于平行四边形来说有特殊情况即特殊的平行四边形，也，这堂课我们就来研究一种恃殊的平行四边形——
有一个角是直角的平行四边形叫做矩形.
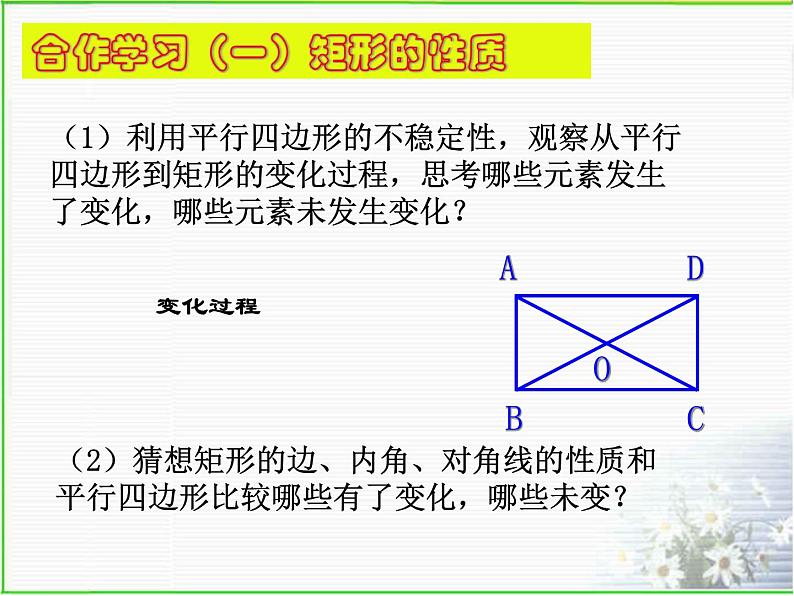
合作学习（一）矩形的性质
（1）利用平行四边形的不稳定性，观察从平行四边形到矩形的变化过程，思考哪些元素发生了变化，哪些元素未发生变化？
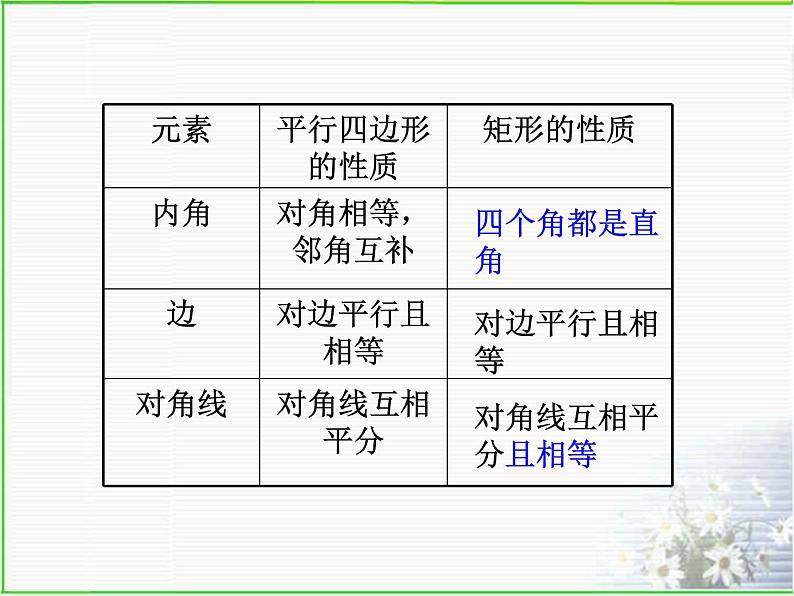
性质1:矩形的四个角都是直角；
已知：四边形ABCD是矩形,∠C= 90°求证：∠A=∠B=∠C=∠D=90°
证明：∵四边形ABCD是矩形， 令∠C=90° ∴∠A=∠C=90° ∠B+∠C=180 ° ∴∠B=180－∠C=90° ∴∠D=∠B=90° 即∠A=∠B=∠C=∠D=90°
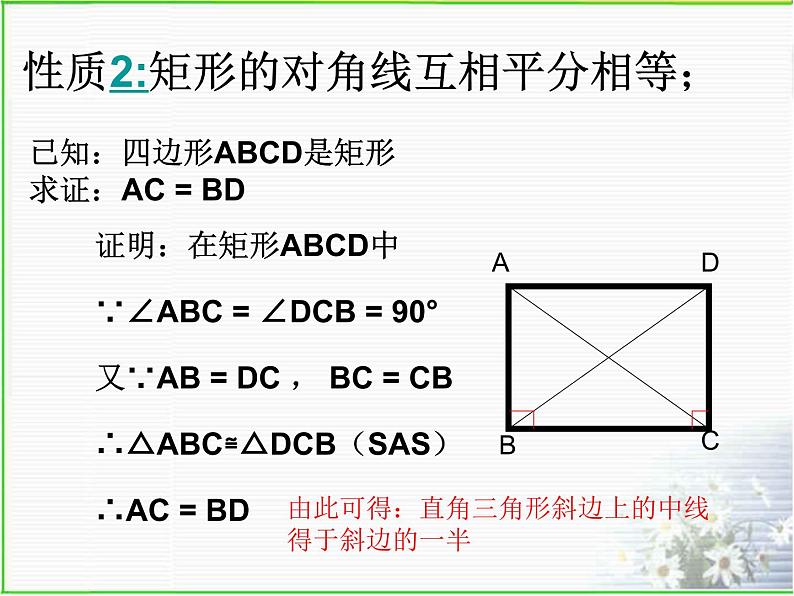
已知：四边形ABCD是矩形 求证：AC = BD
证明：在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC ， BC = CB
∴△ABC≌△DCB（SAS）
性质2:矩形的对角线互相平分相等；
由此可得：直角三角形斜边上的中线得于斜边的一半
任意画一个矩形，请探求它的对称性，如果是中心对称图形，找出它的对称中心，如果是轴对称图形找出它的对称轴。
举例：是轴对称图形的有哪些，是中心对称图形的有哪些，既是轴对称图形又是中心对称图形的有哪些？
性质三：既是轴对称图形又是中心对称图形
问题1：（1）根据矩形的上述性质，你能发现OA、OB、OC、OD有什么关系？
（2）由OA=OB=OC=OD可知图中有几个等腰三角形？这些三角形全等吗?面积相等吗？
（3）若已知BC=8，O到BC的距离为3，求矩形的面积，周长，对角线的长度。
解：OA=OB=OC=OD
∴AC=BD,OA=OC,OD=OB
∴ OA=OB=OC=OD
（3）若∠AOD=120度，AB=4厘米，求矩形的对角线长，周长，面积。
问题2：如图，矩形ABCD的两条对角线相交于点O
（1）若∠AOD=120度，试判断ΔAOB的形状。
（2）若要得到ΔAOB是等边Δ，你可以添加一个什么条件？
四边形ABCD是矩形若已知AB=8㎝，AD=6㎝， 则AC＝ ㎝ OB= ㎝若已知∠CAB=40°，则∠OCB= ∠OBA= ∠AOB= ∠AOD= 若已知AC＝10㎝，BC=6㎝，则矩形的周长＝ ㎝ 矩形的面积＝ ㎝24 若已知 ∠DOC=120°，AD＝6㎝，则AC= ㎝
1.矩形具有而平行四边形不具有的性质（ ）（A）内角和是360度 （B）对角相等（C）对边平行且相等 （D）对角线相等
2.下面性质中，矩形不一定具有的是（ ）（A）对角线相等 （B）四个角相等（C）是轴对称图形 （D）对角线垂直
3.下面图形中，既是轴对称图形，又是中心对称图形的是（ ）（A）角（B）任意三角形（C）矩形（D）等腰三角形
4.由已知矩形的一个顶点向其所对的对角线引垂线，该垂线分直角为3：1两部分，则垂线与另一条对角线的夹角是（ ）（A）60度（B）45度（C）30度（D）22.5度
拓展思维： 1.如图，在矩形ABCD中，AE=BF=3，EF⊥ED交BC于点F，矩形的周长为22，求EF的长.
解：∵在矩形ABCD中， ∴∠A=∠B=90°， ∴∠AED+∠ADE=90 ° ∵ EF⊥ED, ∴∠AED+ ∠BEF=90 ° ∴ ∠ADE= ∠BEF 在△ADE和△BEF中
∠ADE= ∠BEF（已证）
∴ △ADE≌△BEF（AAS）∴AD=BE
∵矩形的周长为22∴AD+AE+BE=11∴BE=4∴EF=5
合作学习（二）矩形的识别
①定义：有一个角是直角的平行四边形是矩形．

应用格式：①∵在平行四边形ABCD中，∠A=90° ∴四边形ABCD是矩形 （有一个角是直角的平行四边形是矩形）
②有三个角是直角的四边形是矩形
已知：如上图， ∠A= ∠ B= ∠ C=90°,试说明：四边形ABCD是矩形。
证明： ∵ ∠A+∠ B=90°+90°=180° ∴AC//BD ∴同理可得AB//CD ∴四边形ABCD是平行四边形（定义） ∴四边形ABCD是矩形 （有一个角是直角的平行四边形是矩形）
应用格式：∵ ∠A= ∠ B= ∠ C=90°, ∴四边形ABCD是矩形 （有三个角是直角的四边形是矩形）
③对角线相等的平行四边形是矩形
说理证明：已知如图：在平行四边形ABCD中，AC=BD.试说明：四边形ABCD是矩形。证明：∵在平行四边形ABCD中 ∴AD=CB, ∠DAB+ ∠CBA=180° 在△DAB和△CBA中
∴ △DAB≌△CBA（SSS）∴ ∠DAB= ∠CBA=90°∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)
应用格式：∵在平行四边形ABCD中，AC=BD. ∴四边形ABCD是矩形（对角线相等的平行四边形是矩形）
④对角线相等且互相平分的四边形是矩形．
说理证明：已知：四边形ABCD中，AC=BD,OA=OC,OB=OD试说明：四边形ABCD是矩形证明：∵OA=OC,OB=OD ∴四边形ABCD是平行四边形 （对角线互相平分的四边形是平行四边形） ∴AD=BC，AD//BC ∴ ∠DAB+ ∠CBA=180°在△DAB和△CBA中
∴△DAB≌△CBA（SSS）
∴ ∠DAB=∠CBA=90°∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)
应用格式：∵ AC=BD,OA=OC,OB=OD ∴四边形ABCD是矩形（对角线相等且互相平分的四边形是矩形）
解:(1)∵在矩形ABCD中 ∴∠BAD=∠ABC=90° ∵AE平分∠BAD ∴ ∠BAE= ∠EAD=45° 即∠1+ ∠CAD=45° ∴ ∠CAD= 45°-15°=30° ∵ AD//BC ∴ ∠2= ∠CAD =30°
解:(2)∵在矩形ABCD中 ∴OB=OA, ∠ABE=90° ∵ ∠BAE45°(第一问已证） ∴ ∠AEB=45 ° ∴ AB=BE又∵ ∠BAO= ∠BAE+ ∠1=60°∴ △ OAB为等边三角形∴AB=OB∴BO=BE