数学九年级下册第5章 对函数的再探索5.4二次函数的图像与性质复习ppt课件

这是一份数学九年级下册第5章 对函数的再探索5.4二次函数的图像与性质复习ppt课件，共32页。PPT课件主要包含了顶点坐标公式，a的作用，ab的作用，c的作用，b2-4ac的作用，抛物线的对称等内容，欢迎下载使用。

通过梳理二次函数的有关练习题，真正掌握好二次函数的图像性质的中考考点。
练习1、 在 y＝－x2， y＝2x2－ ＋3 ， y＝100－5x2， y=－2x2＋5x3－3 中有 个是二次函数。
点评：定义要点 (1)a≠0. (2)最高次数为2. (3)代数式一定是整式.
有 关 练 习
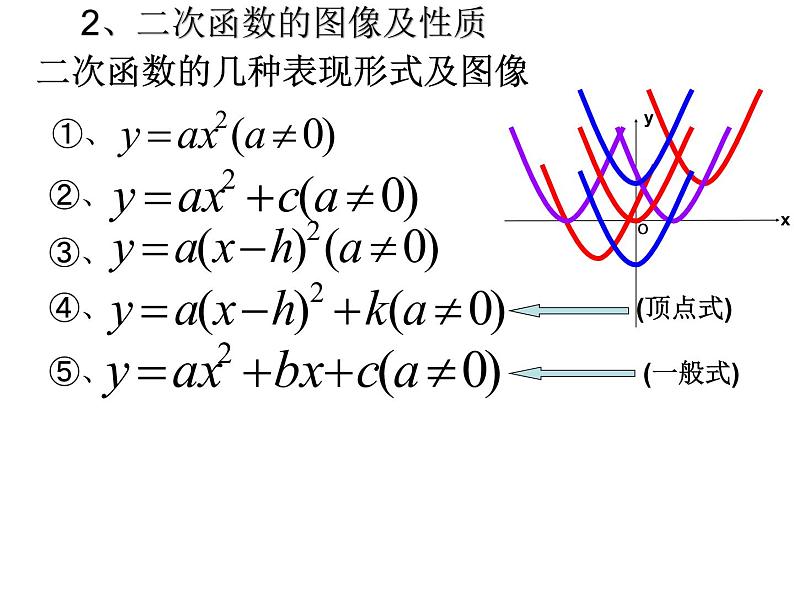
　二次函数的几种表现形式及图像
2、二次函数的图像及性质
4、二次函数　　　　　　　　 图象的顶点坐标和对称轴方程为（　　）A、（1，-2）， x＝1　 B、（1，2)，x＝1C、（-1，-2），x＝-1 D、（-1，2），x＝-1
3、抛物线　　　　　 的对称轴及顶点坐标分别是（ 　）A、y轴，（０，-4）　 B、x＝３，（０，４）C、x轴，（０，０）　　D、y轴，　（０，３）
选择合适的方法求二次函数解析式：
10、抛物线经过（2，0）（0，-2）（-1，0）三点。
11、抛物线的顶点坐标是（6，-2），且与 X轴的一个交点的横坐标是8。
已知顶点坐标、对称轴或最值
已知抛物线与x轴的交点坐标(x1,0).(x2,0)
3、二次函数的图像及性质
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
（1）求抛物线开口方向，对称轴和顶点M的坐标。（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C，A，B的坐标。 （3）x为何值时，y随的增大而减少，x为何值时，y有最大（小）值，这个最大（小）值是多少？（4）x为何值时，y<0？x为何值时，y>0？
当x< -3或x>1时，y > 0
当-3 < x < 1时，y < 0
考点一：对应练习2，真题练,4、13，P66页5
5、函数 　　　　的开口方向 ，顶点坐标是 ，对称轴是 　　 .当x 　 时.y随x的增大而减小。当x 　 时.y有最　　为 .
(1)决定开口方向：a＞０时开口向上，　　　　　　　 a＜０时开口向下.(2)决定形状: ︱a︱相同,则形状相同. ︱a︱不同,则形状不同.(3)决定开口大小: ︱a︱越大,则开口越小. ︱a︱越小,则开口越大.(4)决定最值:a>0时,有最低点,有最小值. a<0时,有最高点,有最大值.(5)决定增减性:a>0时,在对称轴左侧，y随x的增大而减小 在对称轴右侧，y随x的增大而增大. a<0时,在对称轴左侧，y随x的增大而增大在对称轴右侧，y随x的增大而减小.
4、a，b，c符号的确定
a、b同时决定对称轴位置： a、b同号时对称轴在y轴左侧　　　　　　　　　　　　 a、b异号时对称轴在y轴右侧　　　　　　　　　　　　 b＝０时对称轴是y轴
决定抛物线与y轴的交点： c＞０时,抛物线交于y轴的正半轴　　　　　　　　　　　 c＝０时,抛物线过原点　　　　　　　　　　　 c＜０时,抛物线交于y轴的负半轴
决定抛物线与x轴的交点： b2-4ac ＞０时,抛物线与x轴有两个交点　　　　　　　　　　　 b2-4ac ＝０时,抛物线与x轴有一个交点　　　　　　　　　　　 b2-4ac ＜０时,抛物线于x轴没有交点 b2-4ac ≥０时,抛物线于x轴总有交点
二次函数y=ax2+bx+c(a≠0)的几个特例：1）、当x=1 时，2）、当x=-1时，3）、当x=2时，4）、当x=-2时，
6）、2a+b 0. 　
5）、b²-4ac 0. 　
１、二次函数y=ax2+bx+c(a≠0)的图象如图 所示，则a、b、c的符号为（　　） A、a<0,b>0,c>0 B、a<0,b>0,c<0 C、a<0,b<0,c>0 D、a<0,b<0,c<0
2、二次函数y=ax2+bx+c(a≠0)的图象 如图所示，则a、b、c的符号为（　　） A、a>0,b>0,c=0 B、a<0,b>0,c=0 C、a<0,b<0,c<0 D、a>0,b<0,c=0
3、二次函数y=ax2+bx+c(a≠0)的图象如图 所示，则a、b、c 、 △的符号为（ 　） A、a>0,b=0,c>0,△>0 B、a<0,b>0,c<0,△=0 C、a>0,b=0,c<0,△>0 D、a<0,b=0,c<0,△<0
熟练掌握a，b， c，△与抛物线图象的关系
4.抛物线y=ax2+bx+c(a≠0)的图象经过原点和 二、三、四象限，判断a、b、c的符号情况： a 0,b 0,c 0.
5.抛物线y=ax2+bx+c(a≠0)的图象经过原点, 且它的顶点在第三象限，则a、b、c满足 的条件是：a 0,b 0,c 0.
6.二次函数y=ax2+bx+c中，如果a>0，b<0，c<0， 那么这个二次函数图象的顶点必在第 象限
先根据题目的要求画出函数的草图，再根据图象以及性质确定结果（数形结合的思想）
例3，对应练习9,10，真题15
7、如图，在同一坐标系中，函数y=ax+b与 y=ax2+bx(ab≠0)的图象只可能是（ ）
8、二次函数y=ax2+bx+c(a≠0)与一次函数y=ax+c在同一坐标系内的大致图象是（　）
例3，对应练习1、真3，对应练习9,10，真题15
练习⑴二次函数y=2x2的图象向 平移 个单位可得到y=2x2-3的图象；二次函数y=2x2的图象向 平移 个单位可得到y=2(x-3)2的图象。⑵二次函数y=2x2的图象先向 平移 个单位，再向 平移 个单位可得到函数y=2(x+1)2+2的图象。
3、将抛物线y=-3x2-1向上平移2个单位, 再向右平移 3个单位, 所得的抛物线的表达式为 　　　　 ，
4.若把抛物线y=x2+bx+c向左平移3个单位,再向上平移2个单位,得抛物线y=x2-2x+2,则b= ，c= ,
注意：顶点式中，上＋下－，左＋右－
抛物线 关于x轴对称的抛物线解析式是
①将原抛物线写成顶点式y=a(x-h)2+k②写出顶点(h,k)③写出顶点(h,k)关于x轴的点的坐标(h,-k)则关于x轴对称的抛物线解析式是y=-a(x-h)2-k
①将原抛物线写成顶点式y=a(x-h)2+k②写出顶点(h,k)③写出顶点(h,k)关于y轴的点的坐标(-h,k)则关于x轴对称的抛物线解析式是y=a(x+h)2+k
对应练习6，真题7，对应练习4
7.比较函数值的大小：
与x轴有两个不同的交点（x1，0）（x2，0）
有两个不同的解x=x1，x=x2
有两个相等的解x1=x2=
8、二次函数与一元二次方程的关系
例(1)如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=＿＿＿＿,此时抛物线 y=x2-2x+m与x轴有＿＿＿＿个交点.
(2)已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=＿＿＿＿.
(3)一元二次方程 3 x2+x-10=0的两个根是x1= -2 ,x2=5/3, 那么二次函数y= 3 x2+x-10与x轴的交点坐标是＿＿＿＿.
（-2、0）（5/3、0）
1.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的 形状相同,顶点在直线x=1上,且顶点到x轴的距离 为5,请写出满足此条件的抛物线的解析式.
解:抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同  a=1或-1 又顶点在直线x=1上,且顶点到x轴的距离为5,  顶点为(1,5)或(1,-5) 所以其解析式为: (1) y=(x-1)2+5 (2) y=(x-1)2-5 (3) y=-(x-1)2+5 (4) y=-(x-1)2-5 展开成一般式即可.
9、二次函数的综合运用
2.若a+b+c=0,a0,把抛物线y=ax2+bx+c向下平移 4个单位,再向左平移5个单位所到的新抛物线的 顶点是(-2,0),求原抛物线的解析式.
(1)由a+b+c=0可知,原抛物线的图象经过(1,0)
(2) 新抛物线向右平移5个单位, 再向上平移4个单位即得原抛物线
答案:y=-x2+6x-5
12.已知抛物线 y＝x²-mx+m-1.
(1)若抛物线经过坐标系原点，则m______；　　　　　　　
(2)若抛物线与y轴交于正半轴，则m______；　　　　　　　　
(3)若抛物线的对称轴为y轴，则m______。
(4)若抛物线与x轴只有一个交点，则m_______.