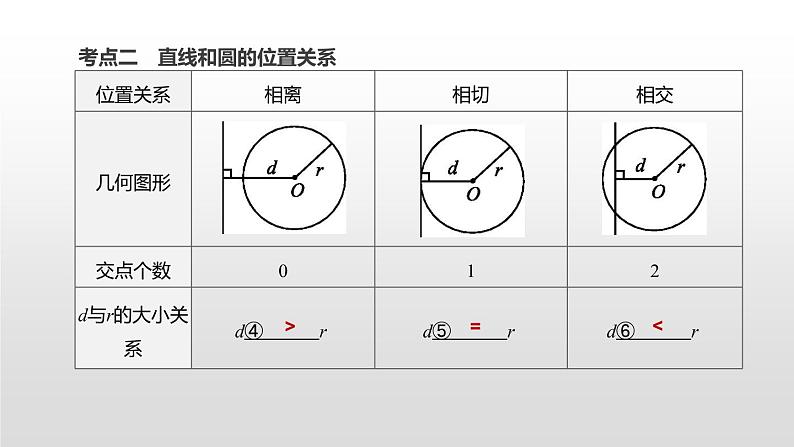
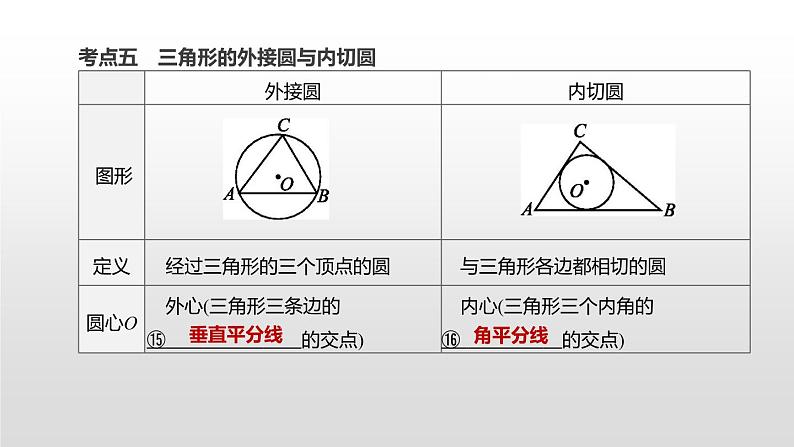
江苏2020中考一轮复习培优 第28课时　与圆有关的位置关系 练习课件

课时训练(二十八)　与圆有关的位置关系

(限时:40分钟)

|夯实基础|

1.[2018·常州] 如图K28-1,AB是☉O的直径,MN是☉O的切线,切点为N,如果∠MNB=52°,则∠NOA的度数为 (　　)

图K28-1

A.76°   B.56°   C.54°   D.52°

2.如图K28-2,AB是☉O的直径,C是☉O上的点,过点C作☉O的切线交AB的延长线于点E,若∠A=30°,则sinE的值为              (　　)

图K28-2

A.    B.    C.    D.

3.[2017·吉林] 如图K28-3,直线l是☉O的切线,A为切点,B为直线l上一点,连接OB交☉O于点C,若AB=12,OA=5,则BC的长为              (　　)

图K28-3

A.15    B.6    C.7    D.8

4.[2017·日照] 如图K28-4,AB是☉O的直径,PA切☉O于点A,连接PO并延长交☉O于点C,连接AC,AB=10,

∠P=30°,则AC的长度是(　　)

图K28-4

A.5   B.5   C.5    D.

5.如图K28-5,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是              (　　)

图K28-5

A.6　　   B.2+1　　 C.9　　   D.

6.在周长为26π的☉O中,CD是☉O的一条弦,AB是☉O的切线,且AB∥CD,若AB和CD之间的距离为18,则弦CD的长为　　　　. 

7.[2017·徐州] 如图K28-6,AB与☉O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=　　　°. 

图K28-6

8.如图K28-7,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:

(1)当d=3时,m=　　　　; (2)当m=2时,d的取值范围是　　　　. 

图K28-7

9.[2018·连云港] 如图K28-8,AB是☉O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=　　　　. 

图K28-8

10.如图K28-9,AB为☉O的直径,延长AB至点D,使BD=OB,DC切☉O于点C,B是的中点,弦CF交AB于点E.若☉O的半径为2,则CF=　　　　. 

图K28-9

11.[2019·鄂州] 如图K28-10,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A,B在x轴上,且OA=OB.点P为☉C上的动点,∠APB=90°,则AB长度的最大值为　　　　. 

图K28-10

12.[2019·黔东南州] 如图K28-11,点P在☉O外,PC是☉O的切线,C为切点,直线PO与☉O相交于点A,B.

(1)若∠A=30°,求证:PA=3PB;

(2)小明发现,∠A在一定范围内变化时,始终有∠BCP=(90°-∠P)成立.请你写出推理过程.

图K28-11

13.[2019·盐城] 如图K28-12,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,以CD为直径的☉O分别交AC,BC于点M,N,过点N作NE⊥AB,垂足为E.

(1)若☉O的半径为,AC=6,求BN的长;

(2)求证:NE与☉O相切.

图K28-12

|拓展提升|

14.[2019·无锡] 如图K28-13,在△ABC中,AC∶BC∶AB=5∶12∶13,☉O在△ABC内自由移动.若☉O的半径为1,且圆心O在△ABC内所能到达的区域的面积为,则△ABC的周长为　　　　. 

图K28-13

15.[2019·宁波] 如图K28-14,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的☉P与△ABC的一边相切时,AP的长为　　　　. 

图K28-14

【参考答案】

1.A

2.A　[解析] 连接OC.

∵CE是☉O的切线,∴OC⊥CE,

∵∠A=30°,∴∠BOC=2∠A=60°,

∴∠E=90°-∠BOC=30°,

∴sinE=sin30°=.故选A.

3.D　[解析] 由切线的性质得OA⊥AB,∵OA=5,AB=12,∴由勾股定理得BO=13,由圆的性质知OC=OA,

∴BC=BO-OC=13-5=8.

4.A　[解析] 过点O作OD⊥AC于点D,由已知条件和圆的性质易求OD的长,再根据勾股定理即可求出AD的长,进而可求出AC的长.

过点O作OD⊥AC于点D,

∵AB是☉O的直径,PA切☉O于点A,

∴AB⊥AP,∴∠BAP=90°,

∵∠P=30°,∴∠AOP=60°,∴∠AOC=120°,∵OA=OC,∴∠OAD=30°,∵AB=10,∴OA=5,∴OD=AO=2.5,

∴AD==,∴AC=2AD=5,故选A.

5.C　[解析] 如图,设半圆O与AC相切于点E,连接OE,作OP1⊥BC,垂足为P1,交半圆O于Q1,

此时垂线段OP1最短,即此时PQ取得最小值,为P1Q1=OP1-OQ1,∵AB=10,AC=8,BC=6,

∴AB2=AC2+BC2,

∴∠C=90°,∵∠OP1B=90°,∠OEC=90°,

∴OP1∥AC,OE∥BC.

∵AO=OB,∴P1C=P1B,AE=EC,

∴OP1=AC=4,OE=BC=3,

∴P1Q1=OP1-OQ1=4-3=1.

当Q2在AB边上,P2与B重合时,

PQ取得最大值,为P2Q2=5+3=8,

∴PQ长的最大值与最小值的和是9.故选C.

6.24　[解析] 如图,设AB与☉O相切于点F,连接OF,OD,延长FO交CD于点E.设☉O的半径为R,

∵2πR=26π,∴R=13,

∴OF=OD=13,

∵AB是☉O的切线,∴OF⊥AB,

∵AB∥CD,∴EF⊥CD,即OE⊥CD,

∴CE=ED,∵EF=18,OF=13,∴OE=5,

在Rt△OED中,

∵∠OED=90°,OD=13,OE=5,

∴ED===12,

∴CD=2ED=24.

7.60　[解析] ∵线段OA与弦BC垂直,

∴BD=BC=1.

在Rt△ABD中,sinA==,∴∠A=30°.

∵AB与☉O相切于点B,∴∠ABO=90°,

∴∠AOB=90°-∠A=60°.

8.(1)1　(2)1<d<3

9.44°　[解析] 连接OB.

∵OA=OB,∴∠OBA=∠OAB=22°,

∴∠AOB=136°,

∵OC⊥OA,∴∠AOC=90°,∴∠COB=46°,

∵CB是☉O的切线,∴∠OBC=90°,

∴∠OCB=90°-46°=44°,故答案为44°.

10.2　[解析] 如图,

连接OC.

∵DC切☉O于点C,

∴∠OCD=90°.

∵BD=OB,∴OB=OD.

∵OC=OB,∴OC=OD,

∴∠D=30°,∴∠COD=60°.

∵AB为☉O的直径,B是的中点,

∴CF⊥OB,CE=EF,∴CE=OC·sin60°=2×=,

∴CF=2.

11.16　[解析] 连接OC并延长,交☉C上一点P,以O为圆心,以OP长为半径作☉O,交x轴于A,B两点,此时AB的长度最大.

∵C(3,4),

∴OC==5.

∵以点C为圆心的圆与y轴相切,

∴☉C的半径为3,

∴OP=OA=OB=8,

∵AB是直径,

∴∠APB=90°,

∴AB长度的最大值为16.

12.解:(1)证明:连接OC.由题意,AB是☉O的直径,∴∠ACB=90°.

∵∠A=30°,∴AB=2BC.

∵OA=OC,

∴∠OCA=∠A=30°,∴∠COP=60°.

∵PC是☉O的切线,

∴∠OCP=90°,∴∠P=30°,

∵∠BOC=60°,OC=OB,

∴∠OBC=∠OCB=60°,

∴∠BCP=30°=∠P,

∴PB=BC,∴AB=2BP,

∴PA=3PB.

(2)∵∠ACB=∠OCP=90°,

∴∠OCA+∠OCB=∠BCP+∠OCB,

∴∠OCA=∠BCP.

∵∠A=∠OCA,∴∠BCP=∠A,

∵∠A+∠P+∠ACB+∠BCP=180°,且∠ACB=90°,

∴2∠BCP=90°-∠P,

∴∠BCP=(90°-∠P).

13.解:(1)∵OD=OC=,∴CD=5.

∵∠ACB=90°,CD是斜边上的中线,

∴AB=2CD=10,

BD=CD=5,

∵AC=6,

∴在Rt△ABC中,BC==8.

连接DN,如图,

∵CD为直径,∴∠DNC=90°,

∴N为BC中点(等腰三角形三线合一),

∴BN=BC=4.

(2)证明:连接NO,

∵BD=CD,∴∠B=∠1.

∵OC=ON,∴∠1=∠2,

∴∠B=∠2,

∴NO∥AB.

∵NE⊥AB,

∴NO⊥NE.

∵ON是半径,

∴NE与☉O相切.

14.25　[解析] 如图,圆心O在△ABC内所能到达的区域是△O1O2O3,易得△ACB∽△O1O2O3,∴它的三边之比也是5∶12∶13,∵△O1O2O3的面积=,∴O1O2=,O2O3=4,O1O3=,连接AO1与CO2,并延长,相交于I,过I作ID⊥AC于D,交O1O2于E,过I作IG⊥BC于G,交O3O2于F,则I是Rt△ABC与Rt△O1O2O3的公共内心,四边形IEO2F与四边形IDCG都是正方形,易知IE=IF=,

∵ED=1,∴ID=IE+ED=,设△ACB的三边分别为5m,12m,13m,则有ID=2m=,解得m=,∴△ABC的周长=30m=25.

15.或3　[解析] 半径为6的☉P与△ABC的一边相切,可能与AC,BC,AB相切,故分类讨论:

①当☉P与AC相切时,点P到AC的距离为6,但点P在线段AD上运动,到AC的最大距离在点D处取到,为5,故这种情况不存在;

②当☉P与BC相切时,点P到BC的距离为6,如图,过P作PE⊥BC于E,PE=6,∴PE为△ACD的中位线,点P为AD中点,在Rt△ACD中,∵AC=12,CD=5,∴AD=13.

∴AP=AD=;

③当☉P与AB相切时,如图,点P到AB的距离为6,过P作PF⊥AB于F,即PF=6,

∵AD=BD=13,∴∠B=∠BAD.∵∠AFP=∠C=90°,∴△APF∽△BAC,∴=,其中,PF=6,AC=12,AB==6,∴AP=3.

综上所述,AP的长为或3.