









广东2020中考数学一轮抢分 1.第一节 线、角、相交线与平行线 课件
展开第四章 三角形
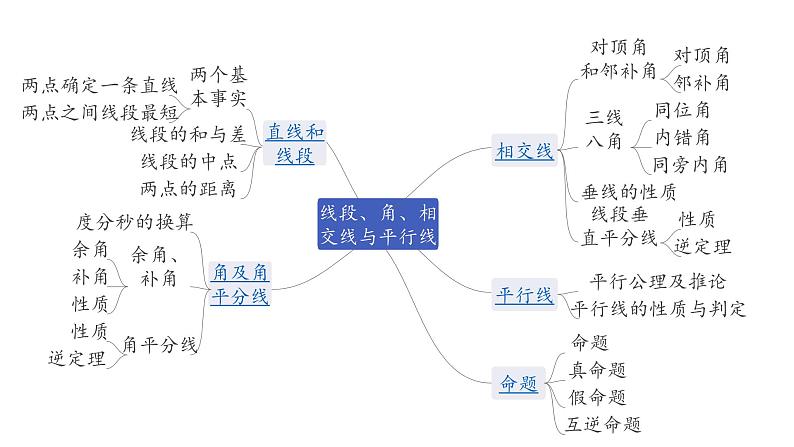
第一节 线、角、相交线与平行线
(建议时间: 分钟)
基础过关
1. 曲桥是我国古代经典建筑之一,它的维修增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图,A,B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( )
A. 两点之间,线段最短 B. 平行于同一条直线的两条直线平行
C. 垂线段最短 D. 两点确定一条直线
第1题图
2. (2019湖州)已知∠α=60°32′,则∠α的余角是( )
A. 29°28′ B. 29°68′ C. 119°28′ D. 119°68′
3. (2019河源模拟)如图,直线AC和直线BD相交于点O,若∠1+∠2=90°,则∠BOC的度数是( )
A. 100° B. 115° C. 135° D. 145°
第3题图
4. (2019湘西州)如图,直线a∥b,∠1=50°,∠2=40°,则∠3的度数为( )
A. 40° B. 90° C. 50° D. 100°
第4题图
5. (2019滨州) 如图,AB∥CD,∠FGB=154°,FG平分∠EFD,则∠AEF的度数等于( )
A. 26° B. 52° C. 54° D. 77°
第5题图
6. (2019襄阳)如图,直线BC∥AE,CD⊥AB于点D,若∠BCD=40°,则∠1的度数是( )
A. 60° B. 50° C. 40° D. 30°
第6题图
7. (2019成都)将等腰直角三角形纸片和矩形纸片按如图方式叠放在一起,若∠1=30°,则∠2的度数为( )
A. 10° B. 15° C. 20° D. 30°
第7题图
- (2019日照)如图,已知AB=8 cm,BD=3 cm,C为AB的中点,则线段CD的长为________cm.
第8题图
- (2019吉林省卷)如图,E为△ABC边CA延长线上一点,过点E作ED∥BC.若∠BAC=70°,∠CED=50°,则∠B=________°.
第9题图
10. (2019安徽)命题“如果a+b=0,那么a,b互为相反数”的逆命题为________________________________________________________________________.
满分冲关
1. (2019铜仁改编) 如图,如果∠1=∠3,∠2=60°,那么∠4的度数为________.
第1题图
2. (2019泰安改编)如图,直线l1∥l2,∠1=30°,则∠2+∠3=________.
第2题图
参考答案
第一节 线、角、相交线与平行线
基础过关
1. A 【解析】∵线段AB比折线AB短,∴原理为两点之间,线段最短.
2. A 【解析】和为90°的两个角互为余角,∵∠α=60°32′,∴∠α的余角为90°-∠α=90°-60°32′=29°28′.
3. C 【解析】∵∠1=∠2,∠1+∠2=90°,∴∠1=∠2=45°,∴∠BOC=180°-∠1=135°.
4. B 【解析】如解图,∵a∥b,∠1=50°,∴∠4=50°.∵∠2=40°,∴∠3=180°-∠2-∠4=90°.
第4题解图
5. B 【解析】∵AB∥CD,∴∠FGB+∠GFD=180°. ∵∠FGB=154°,∴∠GFD=180°-∠FGB=26°. ∵FG平分∠EFD,∴∠EFD=2∠GFD=52°. ∵AB∥CD,∴∠AEF=∠EFD=52°.
6. B 【解析】∵CD⊥AB,∴∠CDB=90°,∵∠BCD=40°,∴∠DBC=50°,∵BC∥AE,∴∠1=∠DBC=50°.
7. B 【解析】如解图,由矩形纸片性质可知两边a∥b,∴∠3=∠1=30°,由等腰直角三角形的性质可知,∠3+∠2=45°,∴∠2=45°-∠3=15°.
第7题解图
8. 1 【解析】∵C为AB的中点,AB=8 cm,∴BC=AB=4 cm,∵BD=3 cm ,∴CD=BC-BD=1 cm.
9. 60 【解析】∵BC∥DE,∴∠CED=∠C=50°,∵∠BAC=70°,∴∠B=180°-∠BAC-∠C=60°.
10. 如果a,b互为相反数,那么a+b=0
满分冲关
1. 120° 【解析】∵∠1=∠3,∴AB∥CD,∴∠5=∠2=60°,∴∠4=180°-∠5=120°.
第1题解图
2. 210° 【解析】 如解图,作l3∥ l1,∵l1∥l2,∴ l3∥l2.∴∠1=∠5=30°,∠4+∠3=180°.∴∠2+∠3=∠5+∠4+∠3=30°+180°=210°.
第2题解图








