广东2020中考数学一轮抢分 3.第三节 反比例函数 课件

第三章　函　数
第三节　 反比例函数(必考，每年1道，3或9分)
考点特训营
目 录
玩转广东8年中考真题
教材改编题
【对接教材】人教：九下第二十六章P1－P22； 北师：九上第六章P148－P162
考点特训营
图象及性质
系数k的几何意义
反比例函数解析式的确定
反比例函数
图象及性质
＞
＜
返回思维导图
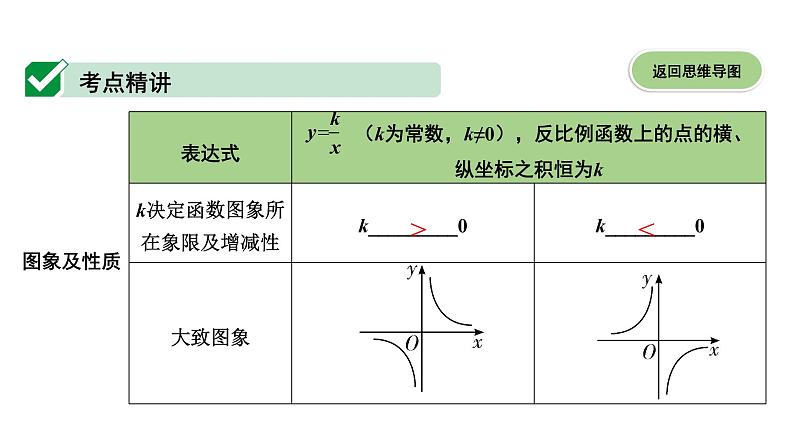
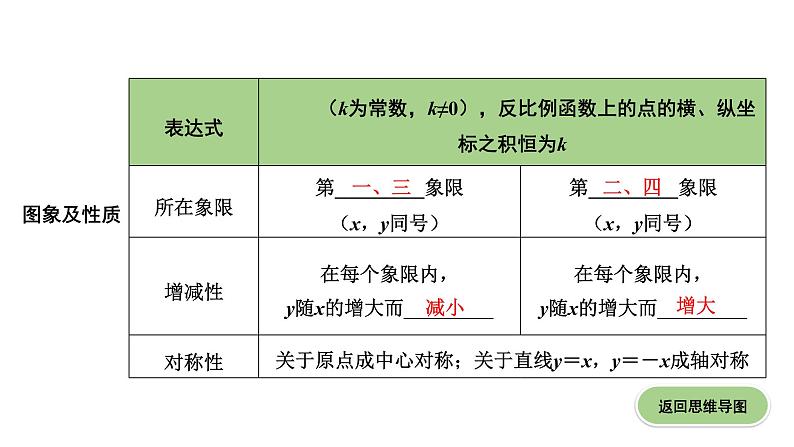
图象及性质
一、三
二、四
减小
增大
返回思维导图
系数k的几何意义
1.系数k的几何意义：如图，过反比例函数图象上任一点P（x，y）作x, 轴、y轴的垂线PM、PN，垂足分别为M、N，所得, 矩形PMON的面积S＝PN·PM＝|x|·|y|＝, |xy|＝_________,
2.常见的反比例函数图象中有关面积的类型见P47微专题类型一
|k|
返回思维导图
反比例函数解析式的确定
1.待定系数法：步骤
（1）设出反比例函数解析式 （k≠0），若题中已给解析式，则不必设；（2）找出反比例函数图象上一点P（a，b）；（3）将点P（a，b）代入解析式得k＝________；（4）确定反比例函数解析式
当已知面积时可考虑用k的几何意义求反比例函数的解析式.由图, 形面积得|k|，再结合图象所在象限判断k的正负，可得k的值，最后, 代入解析式即可
2.利用k的几何意义求解：
ab
返回思维导图
1. 反比例函数y＝ 的图象位于(　　)A. 第一、三象限 B. 第二、三象限 C. 第一、二象限 D. 第二、四象限2. 已知一次函数y＝kx和反比例函数 ，则在同一平面直角坐标系中的函数图象可能是(　　)
A
B
D
k＜0
＜
反比例函数的图象及性质
例 　已知反比例函数 (k≠1)．(1)若该函数图象在第二、四象限时，则k的值可以是(　　)A. 3 B. 2 C. 1 D. －1(2)若该函数图象在每一象限内，y随x的增大而减小，则k的取值范围为________；(3)若点(3，1)在该反比例函数图象上，当y<1时，则x的取值范围是__________；(4)若点A(2，3)与点B(－2，n)都在该函数图象上，则n的值为________；(5)在(4)的条件下，点C(x1，y1)、D(x2，y2)、E(x3，y3)在该函数图象上，若x1＜x2＜0＜x3，则y1、y2、y3的大小关系为___________；
D
k>1
x>3或x<0
－3
y2＜y1＜y3
(6)在(4)的条件下，若点P(x，y)是该反比例函数图象上一点，Q是x轴上一点，且PQ⊥x轴，则△POQ的面积为________；(7)如图，点A是反比例函数 图象上一点，过点A作x轴的平行线，与反比例函数 (x＜0)的图象交于点B(－3，m)．若AB＝4，求该反比例函数的解析式；
例(7)题图
3
(7)解：将点B(－3，m)代入y＝－ 中，得m＝－ ＝1，∴B(－3，1)，∵AB＝4，且AB∥x轴，∴A(1，1)．将点A的坐标代入y＝ 中，得1＝ ，解得k＝2.∴该反比例函数的解析式为y＝ ；
(8)如图，一次函数y＝－x＋3的图象与反比例函数 (k≠1)在第一象限的图象交于A(1，a)和B两点，与x轴交于点C.若点P在x轴上，且△APC的面积为5，求点P的坐标．
例(8)题图
解：把点A(1，a)代入y＝－x＋3，得a＝2，∴A(1，2)把A(1，2)代入反比例函数y＝ ，得k－1＝1×2＝2；∴反比例函数的解析式为y＝ ；∵一次函数y＝－x＋3的图象与x轴交于点C，∴C(3，0)，设P(x，0)，则PC＝|3－x|，∴S△APC＝ |3－x|×2＝5，∴x＝－2或x＝8，∴点P的坐标为(－2，0)或(8，0)．
A
D
C
A
第4题图
6. (2015广东23题9分)如图，反比例函数y＝ (k≠0，x＞0)的图象与直线y＝3x相交于点C，过直线上点A(1，3)作AB⊥x轴于点B，交反比例函数图象于点D，且AB＝3BD.(1)求k的值；(2)求点C的坐标；(3)在y轴上确定一点M，使点M到C、D两点距离之和d＝MC＋MD最小，求点M的坐标．
第6题图
解：(1)当－4＜x＜－1时，一次函数的值大于反比例函数的值；
(3)如解图，设点P的坐标为(x， x＋ )．由△PCA和△PDB面积相等，得 × ·(x＋4)＝ ×1×(2－ x－ )．解得x＝－ .∴y＝ x＋ ＝ .∴点P的坐标为( )．
第7题解图
8. (2019广东23题9分)如图，一次函数y＝k1x＋b的图象与反比例函数y＝ 的图象相交于A、B两点，其中点A的坐标为(－1，4)，点B的坐标为(4，n)．(1)根据图象，直接写出满足k1x＋b＞ 的x的取值范围；(2)求这两个函数的表达式；(3)点P在线段AB上，且S△AOP∶S△BOP＝1∶2，求点P的坐标．
第8题图
解：(1)x<－1或0(3)如解图，连接OP、OA、OB，设直线y＝－x＋3与x轴交于点C，∵当y＝0时，x＝3，∴点C的坐标为(3，0)．∵S△AOB＝S△AOC＋S△BOC，∴S△AOB＝ ×3×4＋ ×3×1＝ .∵S△AOP∶S△BOP＝1∶2，∴S△BOP＝ S△AOB＝ ＝5.∵点P在线段AB上，设P的坐标为(m，－m＋3)，S△POB＝S△POC＋S△BOC，∴S△BOP＝ ×3·(－m＋3)＋ ×3×1＝5，∴解得m＝ ，∴－m＋3＝－ ＋3＝ ，∴点P的坐标为( )．
(4)如图③，直线l与x轴，y轴分别交于A、B两点，与反比例函数y＝ (x＞0)的图象交于点C，连接OC，若S△AOB＝S△BOC＝1，求m的值．
(4)如解图②，过点C作CD⊥x轴于D，设OB＝a(a＞0)．∵S△AOB＝S△BOC，∴AB＝BC.∵△AOB的面积为1，∴ OA·OB＝1，∴OA＝ ，∵CD∥OB，AB＝BC，∴OD＝OA＝ ，CD＝2OB＝2a，∴C( ，2a)，∵反比例函数y＝ (x＞0)的图象经过点C，∴1－2m＝ ×2a＝4.解得m＝－ .
第1题解图②