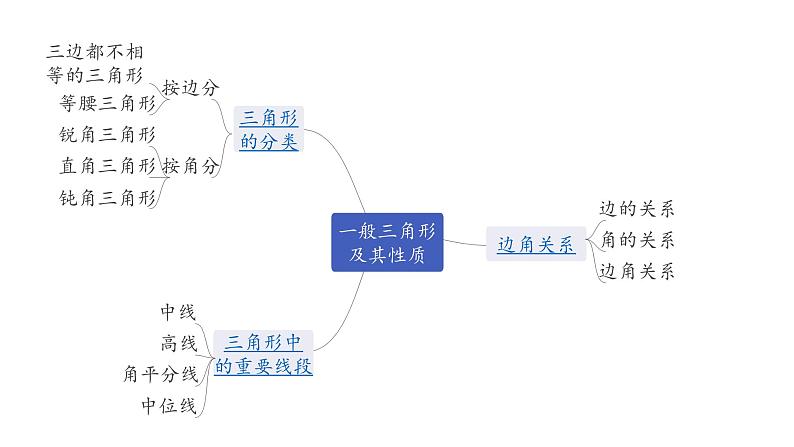
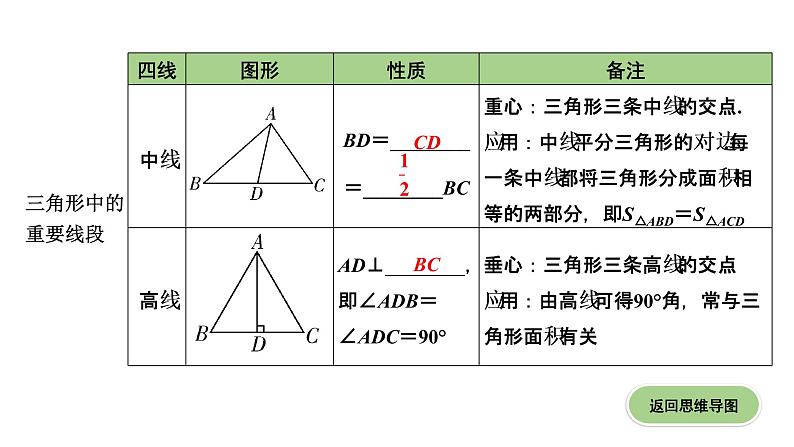
广东2020中考数学一轮抢分 2.第二节 一般三角形及其性质 课件

第四章  三角形

第二节 一般三角形及其性质

（建议时间：     分钟）

基础过关

1. (2019百色)三角形的内角和等于(　　)

A. 90°  B. 180°  C. 270°  D. 360°

2. (2019贵州三州联考)在下列长度的三条线段中，不能组成三角形的是(　　)

A. 2 cm，3 cm，4 cm  B. 3 cm，6 cm，6 cm  C. 2 cm，2 cm，6 cm  D. 5 cm，6 cm，7 cm

3. (2019自贡)已知三角形的两边长分别为1和4，第三边长为整数，则该三角形的周长为(　　)

A. 7  B. 8  C. 9  D. 10

4. (2019绍兴)如图，墙上钉着三根木条a，b，c，量得∠1＝70°，∠2＝100°，那么木条a，b所在直线所夹的锐角是(　　)

A. 5°  B. 10°  C. 30°  D. 70°

第4题图

5. (2019泰州)如图所示的网格由边长相同的小正方形组成，点A、B、C、D、E、F、G在小正方形的顶点上，则△ABC的重心是(　　)

A. 点D  B. 点E  C. 点F  D. 点G

第5题图

6. (2019荆门)将一副直角三角板按如图所示的位置摆放，使得它们的直角边互相垂直，则∠1的度数是(　　)

A. 95°  B. 100°  C. 105°  D. 110°

第6题图

7. (2019杭州)在△ABC中，若一个内角等于另两个内角的差，则(　　)

A. 必有一个内角等于30°  B. 必有一个内角等于45°

C. 必有一个内角等于60°  D. 必有一个内角等于90°

8. 如图，在△ABC中，AB＝6，AC＝10，AD平分∠BAC，BD⊥AD于点D，BD的延长线交AC于点F，E为BC的中点，则DE的长为(　　)

A. 2  B. 3  C. 4  D. 5

第8题图

9. (2019大庆)如图，在△ABC中，BE是∠ABC的平分线，CE是外角∠ACM的平分线，BE与CE相交于点E，若∠A＝60°，则∠BEC是(　　)

A. 15°  B. 30°  C. 45°  D. 60°

第9题图

10. (2018黄石)如图，△ABC中，AD是BC边上的高，AE、BF分别是∠BAC、∠ABC的平分线，∠BAC＝50°，∠ABC＝60°，则∠EAD＋∠ACD＝(　　)

A. 75°  B. 80°  C. 85°  D. 90°

第10题图

11. (2019青岛)如图，BD是△ABC的角平分线，AE⊥BD，垂足为F.若∠ABC＝35°，∠C＝50°，则∠CDE的度数为(　　)

A. 35°  B. 40°  C. 45°  D. 50°

第11题图

12. (2019梧州)如图，已知在△ABC中，D、E分别是AB、AC的中点，F、G分别是AD、AE的中点，且FG＝2 cm，则BC的长度是________cm.

第12题图

13. 如图，△ABC的面积是4，点D、E、F分别是BC、AD、BE的中点，则△CEF的面积是________．

第13题图

14. (2019铜仁)如图，在△ABC中，D是AC的中点，且BD⊥AC，ED∥BC，ED交AB于点E，BC＝7 cm，AC＝6 cm，则△AED的周长等于________cm.

第14题图

15. 如图，△ABC的面积为30，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD＝3，则△ABC的周长为________．

第15题图

满分冲关

1. (2019湖州)如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝9，CD＝4，则四边形ABCD的面积是(　　)

A. 24  B. 30

C. 36  D. 42

第1题图

2. 在△ABC中，AB＝，AC＝5，若BC边上的高等于3，则BC边的长为________．

3. (2019攀枝花)如图，在△ABC中，CD是AB边上的高，BE是AC边上的中线，且BD＝CE.

求证：(1)点D在BE的垂直平分线上；

(2)∠BEC＝3∠ABE.

第3题图

核心素养提升

海伦——秦九韶公式

1. (2019宜昌)古希腊几何学家海伦和我国南宋数学家秦九韶都曾提出利用三角形的三边求面积的公式，称为海伦－秦九韶公式：如果一个三角形的三边长分别是a，b，c，记p＝，那么三角形的面积为S＝.如图，在△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，若a＝5，b＝6，c＝7，则△ABC的面积为(　　)

A. 6

B. 6

C. 18

D.

第1题图

参考答案

第二节 一般三角形及其性质

基础过关

1. B

2. C　【解析】根据三角形三边关系，两边之和大于第三边，两边之差小于第三边，2 cm, 2 cm, 6 cm中6 cm最长，而6 > 2＋2，不能构成三角形，故选C.

3. C　【解析】设这个三角形的第三边长为c，则4－1<c<4＋1，即3<c<5，∵c是整数，∴c＝4，∴这个三角形的周长为1＋4＋4＝9.

4. B　【解析】如解图，∵∠2＝100°，∴∠3＝∠2＝100°，又∵∠1＝70°，∴∠1＋∠3＝170°≠180°，∴两直线不平行，∴木条a，b所在直线所夹的锐角为180°－(∠1＋∠3)＝10°.

第4题解图

5. A　【解析】三角形的重心为三角形三条边中线的交点，如解图，AB边和AC边及BC边上的中线，它们相交于点D.

第5题解图

6. C　【解析】如解图，∵∠3＝∠2＝45°，∠4＝60°，∴∠1＝∠3＋∠4＝105°.

第6题解图

7. D　【解析】设这三个内角分别为∠A，∠B，∠C，则∠A＝∠B－∠C，移项得∠A＋∠C＝∠B，∵∠A＋∠B＋∠C＝180°，∴2∠B ＝180°，∴∠B ＝90°.即必有一个内角等于90°.

8. A　【解析】∵AD平分∠BAC，BD⊥AD，∴AF＝AB＝6，BD＝DF，∴CF＝AC－AF＝4，∵BD＝DF，E为BC的中点，∴DE是△BCF的中位线，∴DE＝CF＝2.

9. B　【解析】∵BE是∠ABC的平分线，CE是∠ACM的平分线，∴∠CBE＝∠ABC，∠ECM＝∠ACM，∵∠BEC＝∠ECM－∠CBE，∴∠BEC＝(∠ACM－∠ABC)，∵∠ACM＝∠A＋∠ABC＝60°＋∠ABC，∴∠BEC＝(60°＋∠ABC－∠ABC)＝30°.

10. A　【解析】根据三角形内角和知∠C＝180°－∠ABC－∠BAC＝180°－60－50°＝70°，又∵AD⊥BC，∴∠DAC＝90°－70°＝20°，又∵AE为∠BAC的平分线，∴∠EAC＝∠BAC＝25°，则∠EAD＝∠EAC－∠DAC＝5°，∴∠EAD＋∠ACD＝75°.

11. C　【解析】∵BD是△ABC的角平分线，AE⊥BD，∴∠ABD＝∠CBD＝∠ABC＝17.5°，∠AFB＝∠EFB＝90°，∴∠BAF＝∠BEF，∴AB＝BE，∴AF＝EF，∴AD＝ED，∴∠DAF＝∠DEF，∵∠BAC＝180°－∠ABC－∠C＝95°，∴∠BED＝∠BAD＝95°，∴∠CDE＝95°－50°＝45°.

12. 8　【解析】∵D、E分别是AB、AC的中点，∴DE＝BC.又∵F、G分别是AD、AE的中点，∴FG＝DE，∴BC＝4FG＝8.

13. 1　【解析】∵S△ABC＝4，点E是AD的中点，∴S△BCE＝S△ABC＝×4＝2，又∵点F是BE的中点，∴S△CEF＝S△BCE＝×2＝1.

14. 10　【解析】∵BD⊥AC，AD＝CD＝3 cm，∴BD垂直平分AC，∴AB＝BC＝7cm，∵DE∥BC，∴AE＝BE＝3.5 cm，且DE＝BC＝3.5 cm，∴△AED的周长为AE＋ED＋AD＝3.5＋3.5＋3＝10 cm.

15. 20　【解析】如解图，连接OA，∵OB、OC分别平分∠ABC和∠ACB，∴点O到边AB、AC、BC的距离都相等，∵OD⊥BC，且OD＝3，S△ABC＝(AB＋BC＋AC)·OD＝30，∴AB＋BC＋AC＝20.即△ABC的周长为20.

第15题解图

满分冲关

1. B　【解析】∵BD平分∠ABC，∠BCD＝90°，CD＝4，∴点D到AB的距离为4，∵BC＝9，AB＝6，∴S四边形ABCD＝S△ABD＋S△CBD＝AB·CD＋BC·CD＝×6×4＋×9×4＝30.

2. 9或1　【解析】如解图①，当BC边上的高AD在△ABC内时，在Rt△ACD中，AC＝5，AD＝3，由勾股定理得CD＝＝4，在Rt△ABD中，AB＝，AD＝3，由勾股定理得BD＝＝5，则BC＝BD＋CD＝9；如解图②，BC边上的高AD在△ABC的外部时，则点D一定在BC的延长线上，此时BC＝BD－CD＝1.综上，BC边的长为9或1.

第2题解图

3. 证明：(1)如解图，连接DE.

∵CD是AB边上的高，

∴CD⊥AB，

∴∠ADC＝90°.

∵BE是AC边上的中线，

∴AE＝CE.

∴DE＝AC＝CE＝AE.

∵BD＝CE，

∴DE＝BD，

∴点D在BE的垂直平分线上；

(2)∵BD＝DE，

∴∠DBE＝∠DEB.

∴∠ADE＝2∠ABE＝2∠DEB.

∵DE＝AE，

∴∠A＝∠ADE＝2∠ABE.

∴∠BEC＝∠ABE＋∠A＝3∠ABE.

第3题解图

核心素养提升

1. A　【解析】由题可知，p＝＝＝9，∴S△ABC＝＝＝6.