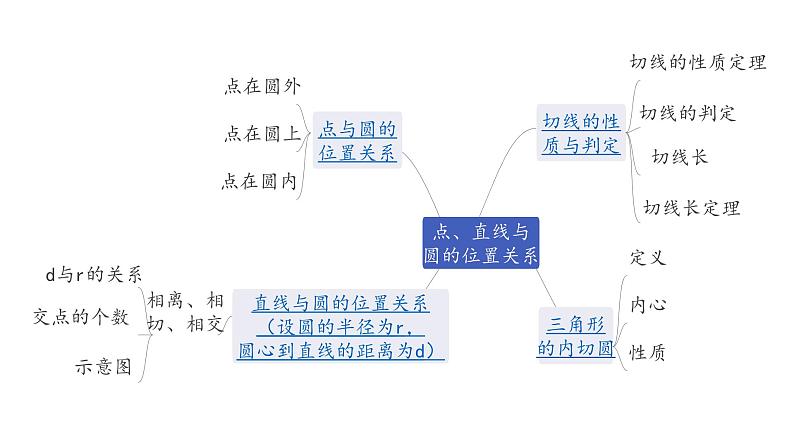
广东2020中考数学一轮抢分 2.第二节 点、直线与圆的位置关系 课件

第六章  圆

第二节 点、直线与圆的位置关系

（建议时间：     分钟）

基础过关

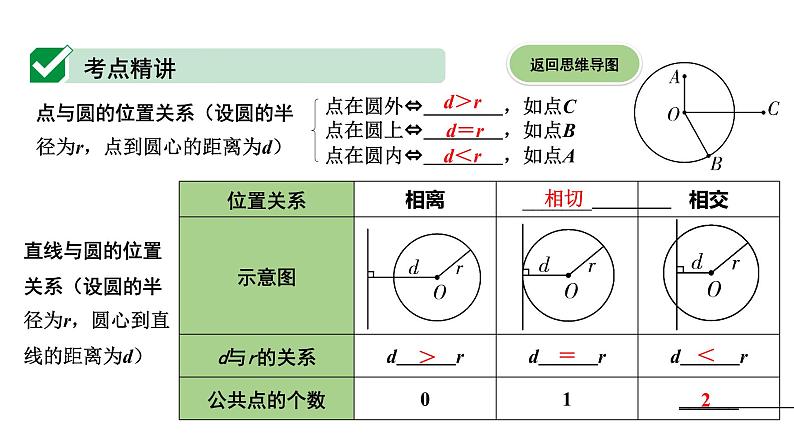
1. 已知⊙O的半径为5 cm，圆心O到直线l的距离为5 cm，则直线l与⊙O的位置关系为(　　)

A. 相交  B. 相切  C. 相离  D. 无法确定

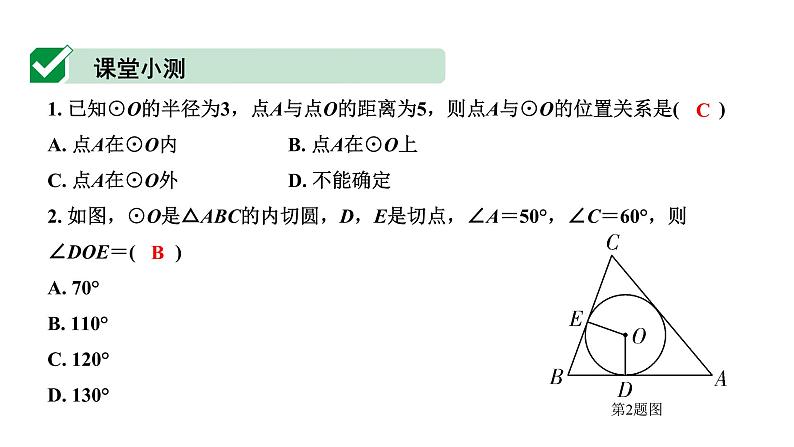
2. (2019梅州模拟)如图，直线l是⊙O的切线，A为切点，B为直线l上一点，连接OB交⊙O于点C.若AB＝12，OA＝5，则BC的长为(　　)

A. 5  B. 6  C. 7  D. 8

第2题图

3. (2019重庆A卷)如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙O交于点D，连接OD，若∠C＝50°，则∠AOD的度数为(　　)

A. 40°  B. 50°  C. 80°  D. 100°

第3题图

4. (2019台州)如图，等边三角形ABC的边长为8，以BC上一点O为圆心的圆分别与边AB，AC相切，则⊙O的半径为(　　)

A. 2  B. 3  C. 4  D. 4－

第4题图

5. (2019宿迁)直角三角形的两条直角边分别为5和12，则它的内切圆半径为________．

6. (2019河池)如图，PA，PB是⊙O的切线，A，B为切点，∠OAB＝38°，则∠P＝________°.

第6题图

7. (2019徐州)如图，AB为⊙O的直径，C为⊙O上一点，D为的中点，过点D作直线AC的垂线，垂足为E，连接OD.

(1)求证：∠A＝∠DOB；

(2)DE与⊙O有怎样的位置关系？请说明理由．

第7题图

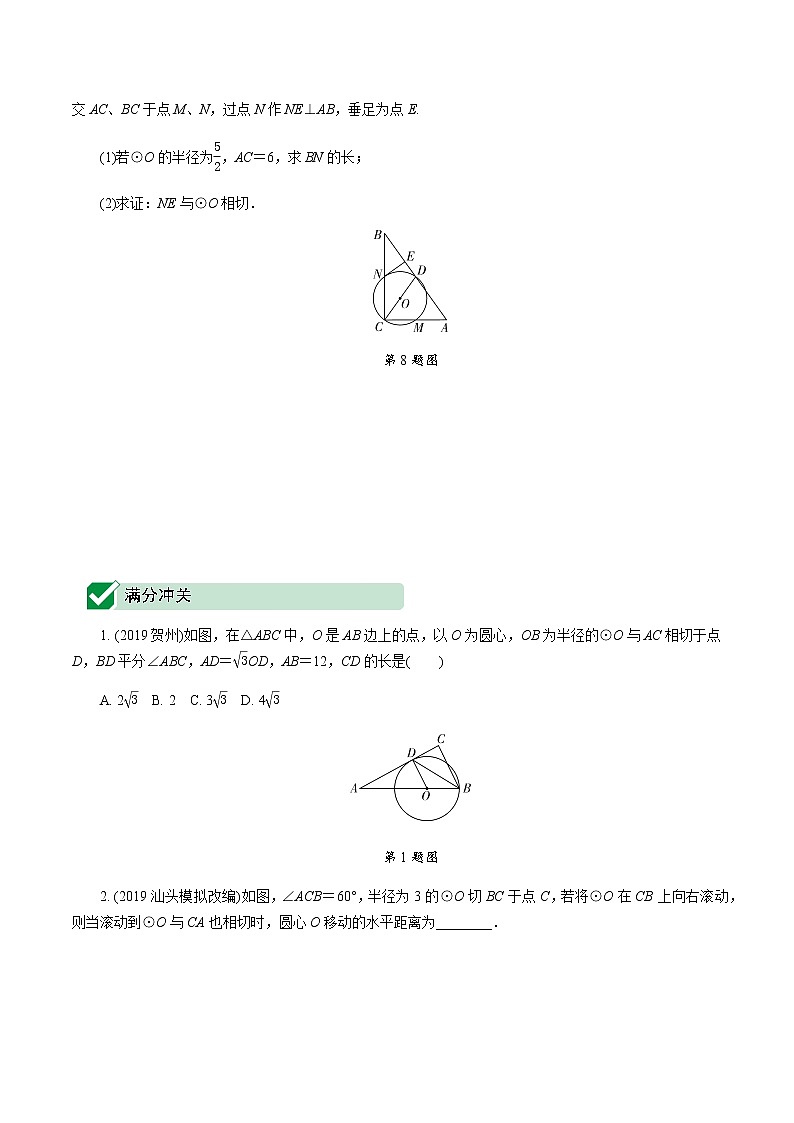
8. (2019盐城)如图，在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，以CD为直径的⊙O分别交AC、BC于点M、N，过点N作NE⊥AB，垂足为点E.

(1)若⊙O的半径为，AC＝6，求BN的长；

(2)求证：NE与⊙O相切．

第8题图

满分冲关

1. (2019贺州)如图，在△ABC中，O是AB边上的点，以O为圆心，OB为半径的⊙O与AC相切于点D，BD平分∠ABC，AD＝OD，AB＝12，CD的长是(　　)

A. 2  B. 2  C. 3  D. 4

第1题图

2. (2019汕头模拟改编)如图，∠ACB＝60°，半径为3的⊙O切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离为________．

第2题图

3. (2019中山模拟)如图，AD是⊙O的切线，切点为A，AB是⊙O的弦，过点B作BC∥AD，交⊙O于点C，连接AC，过点C作CD∥AB，交AD于点D，连接AO并延长交BC于点M，交过点C的直线于点P，且∠BCP＝∠ACD.

(1)求证：MB＝MC；

(2)求证：直线PC是⊙O的切线；

(3)若AB＝9，BC＝6，求PC的长．

第3题图

核心素养提升

《九章算术》——勾股容圆

1. 《九章算术》是东方数学思想之源，该书中记载：“今有勾八步，股一十五步，问勾中容圆径几何？”其意思是：“今有直角三角形，勾(短直角边)长为8步，股(长直角边)长为15步，问该直角三角形内切圆的直径是多少步．”该问题的答案是________步．

参考答案

第二节 点、直线与圆的位置关系

基础过关

1. B

2. D　【解析】由勾股定理得OB＝＝13，∴BC＝OB－OC＝13－5＝8.

3. C　【解析】∵AB是⊙O的直径，AC与⊙O相切于点A，∴∠BAC＝90°.∵∠C＝50°，∴∠ABD＝40°.∴∠AOD＝2∠ABD＝80°.

4. A　【解析】如解图，设⊙O分别与AB，AC相切于点M、N，连接OM、ON，∴∠BMO＝∠CNO＝90°.又∵∠B＝∠C，OM＝ON，∴△BMO≌△CNO(AAS)．∴OB＝OC＝4.又∵∠B＝60°，∴OM＝2，即⊙O的半径为2.

第4题解图

5. 2　【解析】∵两条直角边的长分别为5和12，由勾股定理可知，斜边长＝＝13，∴它的内切圆的半径＝＝2.

6. 76　【解析】如解图，连接OB，∵PA，PB是⊙O的切线，∴∠OAP＝∠OBP＝90°.∵AO＝BO，∴∠OBA＝∠OAB＝38°.∴∠AOB＝180°－38°－38°＝104°.在四边形AOBP中，∠P＝360°－90°×2－104°＝76°.

第6题解图

7. (1)证明：如解图，连接OC，

∵OC＝OA，

∴∠A＝∠ACO.

∵∠COB是△AOC的外角，

∴∠COB＝∠A＋∠ACO＝2∠A.

∵D为的中点，

∴＝.

∴∠COD＝∠DOB.

∵∠COB＝∠COD＋∠DOB＝

2∠DOB，

∴∠A＝∠DOB；

(2)解：DE与⊙O相切．

理由如下：

∵由(1)得∠A＝∠DOB，

∴AE∥OD.

∴∠E＋∠EDO＝180°.

∵DE⊥AE，

∴∠ODE＝90°.

∵OD是⊙O的半径，

∴DE是⊙O的切线．

第7题解图

8. (1)解：如解图，连接DN.

∵∠ACB＝90°，CD是斜边AB的中线，

∴CD＝AD＝BD，

∵CD是⊙O的直径，

∴∠DNC＝90°＝∠ACB，

∴DN∥AC，

∴BN＝BC，

∵⊙O的半径为，

∴CD＝5，

∴AB＝2CD＝10，

在Rt△ABC中，BC＝＝＝8，

∴BN＝4；

(2)证明：如解图，连接ND，ON.

∵BN＝CN，OC＝OD，

∴ON∥BD.

∵NE⊥DB，

∴NE⊥ON.

又∵ON为⊙O的半径，

∴NE与⊙O相切．

第8题解图

满分冲关

1. A　【解析】∵AD是⊙O的切线，∴OD⊥AD，在Rt△AOD中，AD＝OD，∴tan∠A＝＝＝.∴∠A＝30°.∴∠AOD＝60°，∵OD＝OB，∴∠ODB＝∠ABD＝∠AOD＝30°.∵BD平分∠ABC，∴∠CBD＝∠ABD＝30°.∴∠ABC＝60°.∴∠C＝90°.在Rt△ABC中，sin∠A＝，AB＝12，∴BC＝AB·sin∠A＝12×＝6. 在Rt△CBD中，CD＝BC·tan∠CBD＝6×＝2.

2. 3　【解析】设⊙O与CA相切于点P，此时和CB相切于点D，连接OC、OD、OP.∵⊙O与CA相切，⊙O与CB相切，∴∠OCD＝∠ACB＝30°，∵OD＝3，∴CD＝＝3，即圆心O移动的水平距离为3.

第2题解图

3. (1)证明：∵AD是⊙O的切线，

∴OA⊥AD.

∵BC∥AD，

∴OA⊥BC.

∴MB＝MC；

(2)证明：如解图，过C点作直径CF，连接FB，

 ∵CF为直径，

∴∠FBC＝90°，即∠F＋∠BCF＝90°.

∵AB∥DC，

∴∠ACD＝∠BAC.

∵∠BAC＝∠F，∠BCP＝∠ACD，

∴∠F＝∠BCP.

∴∠BCP＋∠BCF＝90°，即∠PCF＝90°.

∴CF⊥PC，

∵OC为⊙O的直径，

∴直线PC是⊙O的切线；

(3)解：由(1)知BM＝CM＝BC＝3，AM⊥BC，

∴AC＝AB＝9.

在Rt△AMC中，AM＝＝6，

设⊙O的半径为r，则OC＝r，OM＝AM－r＝6－r，

在Rt△OCM中，OM2＋CM2＝OC2，即(6－r)2＋32＝r2，

解得r＝，

∴CF＝2r＝，OM＝6－＝.∴BF＝2OM＝.

∵∠F＝∠MCP，∠PMC＝∠FBC＝90°，

∴△PCM∽△CFB.

∴＝.

∴＝，

∴PC＝.

第3题解图

核心素养提升

1. 6　【解析】由勾股定理得，斜边＝＝17.如解图，⊙O是△ABC的内切圆，AB＝8，BC＝15，AC＝17，设⊙O的半径为r，则BE＝OE＝OF＝BF＝OG＝r，AE＝AG，CG＝CF，∴CF＝AC－AG＝AC－(AB－r)，即15－r＝17－(8－r)，解得2r＝15＋8－17＝6，即直角三角形内切圆的直径是6.

第1题解图

如需查看更多内容，请微信扫上方二维码获取