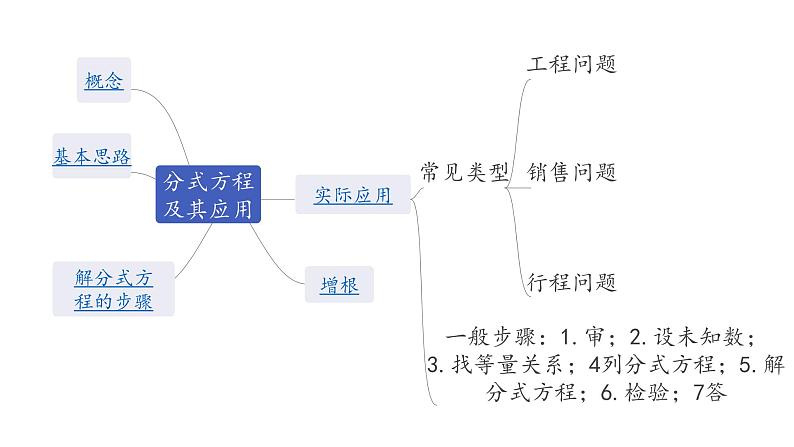
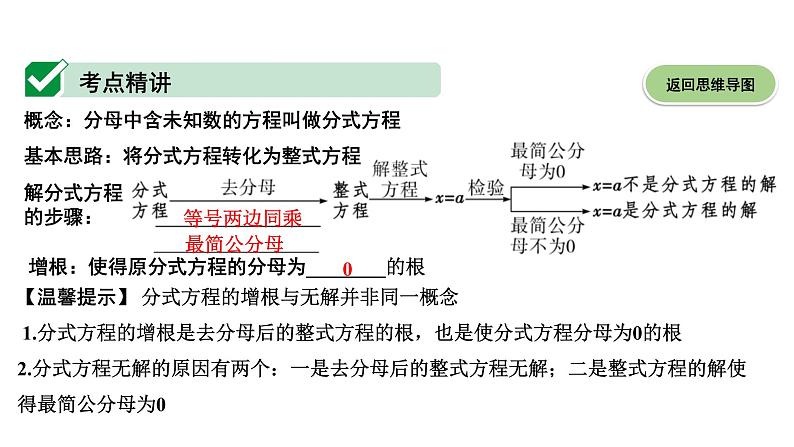
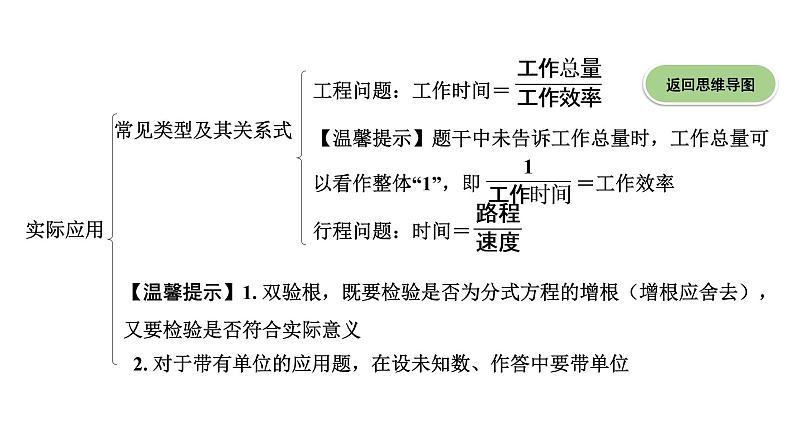
广东2020中考数学一轮抢分 2.第二节 分式方程及其应用 课件

第二章  方程（组）与不等式（组）

第二节 分式方程及其应用

（建议时间：     分钟）

基础过关

1. (2019百色)方程＝1的解是(　　)

A. 无解  B. x＝－1  C. x＝0  D. x＝1

2. (2019淄博)解分式方程＝－2时，去分母变形正确的是(　　)

A. －1＋x＝－1－2(x－2)  B. 1－x＝1－2(x－2)

C. －1＋x＝1＋2(2－x)  D. 1－x＝－1－2(x－2)

3. (2019成都)分式方程＋＝1的解为(　　)

A. x＝－1  B. x＝1  C. x＝2  D. x＝－2

4. (2019 湘潭)现代互联网技术的广泛应用，催生了快递行业的高速发展．据调查，湘潭某家小型快递公司的分拣工小李和小江，在分拣同一类物件时，小李分拣120个物件所用的时间与小江分拣90个物件所用的时间相同，已知小李每小时比小江多分拣20个物件，若设小江每小时分拣x个物件，则可列方程为(　　)

A. ＝  B. ＝  C. ＝  D. ＝

5. (2019十堰)十堰即将跨入高铁时代，钢轨铺设任务也将完成，现还有6000米的钢轨需要铺设，为确保年底通车，如果实际施工时每天比原计划多铺设20米，就能提前15天完成任务，设原计划每天铺设钢轨x米，则根据题意所列的方程是(　　)

A. －＝15  B. －＝15

C. －＝20  D. －＝20

6. (2019烟台)若关于x的分式方程－1＝有增根，则m的值为________．

7. (2019江西)斑马线前“车让人”，不仅体现着一座城市对生命的尊重，也直接反映着城市的文明程度．如图，某路口的斑马线路段A－B－C横穿双向行驶车道，其中AB＝BC＝6米，在绿灯亮时，小明共用11秒通过AC，其中通过BC的速度是通过AB速度的1.2倍，求小明通过AB时的速度．设小明通过AB时的速度是x米/秒，根据题意列方程得：__________________．

第7题图

8. (2019南京)解方程－1＝.

9. (2019毕节)解方程：1－＝.

10. (2019日照)“一带一路”战略给沿线国家和地区带来很大的经济效益，某企业的产品对沿线地区实行优惠，决定在原定价基础上每件降价40元，这样按原定价需花费5000元购买的产品，现在只花费了4000元．求每件产品的实际定价是多少？

满分冲关

1. (2019荆州)已知关于x的分式方程－2＝的解为正数，则k的取值范围为(　　)

A. －2<k<0  B. k>－2且k≠－1  C. k>－2  D. k<2且k≠1

2. 某乡镇决定对一段公路进行改造．已知这项工程由甲工程队单独做需要40天完成；如果由乙工程队先单独做10天，那么剩下的工程还需要两队合作20天才能完成．

(1)求乙工程队单独完成这项工程所需的天数；

(2)求两队合作完成这项工程所需的天数．

3. (2018玉林)山地自行车越来越受中学生的喜爱．一网店经营的某型号山地自行车，今年一月份销售额为30000元，二月份每辆车售价比一月份每辆车售价降价100元，若销售的数量与上一月销售的数量相同，则销售额是27000元．

(1)求二月份每辆车售价是多少元？

(2)为了促销，三月份每辆车售价比二月份每辆车售价降低了10%，网店仍可获利35%，求每辆山地自行车的进价是多少元？

核心素养提升

1. 在求3x的倒数的值时，嘉淇同学误将3x看成了8x，她求得的值比正确答案小5，依上述情形，所列关系式成立的是(　　)

A. ＝－5  B. ＝＋5  C. ＝8x－5  D. ＝8x＋5

2. 对于非零实数a、b，规定a⊗b＝－.若x⊗(2x－1)＝1，则x的值为(　　)

A. 1  B.   C. －1  D. －

参考答案

第二节 分式方程及其应用

基础过关

1. C　【解析】方程两边同乘(x＋1)，得1＝x＋1，解得x＝0.

2. D　【解析】分式方程＝－2去分母，也就是两边同乘(x－2)，得1－x＝－1－2(x－2)．

3. A　【解析】给方程两边同乘x(x－1)得x(x－5)＋2(x－1)＝x(x－1)，去括号得x2－5x＋2x－2＝x2－x，即－2x＝2，解得x＝－1.经检验，x＝－1是原分式方程的解．

4. B　【解析】∵小江每小时分拣x个物件，小李每小时比小江多分拣20个物件，∴小李每小时分拣(x＋20)个物件．根据等量关系“小李分拣120个物件所用的时间与小江分拣90个物件所用的时间相同”可列方程＝.

5. A　【解析】根据题意可得：－＝15.

6. 3　【解析】给分式方程去分母，得3x－(x－2)＝m＋3，去括号，得3x－x＋2＝m＋3，合并同类项，得2x＝m＋1，∴m＝2x－1.∵原分式方程有增根，∴x－2＝0.∴x＝2.∴m＝2x－1＝2×2－1＝3.

7. ＋＝11　【解析】依题意，小明通过AB段和BC段的时间可以分别表示为秒、秒，故可列方程为＋＝11.

8. 解：方程两边同乘(x－1)(x＋1)，得x(x＋1)－(x－1)(x＋1)＝3，

去括号，得x2＋x－x2＋1＝3，

移项，得x2＋x－x2＝3－1，

合并同类项，得x＝2.

检验：当x＝2时，(x－1)(x＋1)≠0.

∴原分式方程的解为x＝2.

9. 解：方程两边同乘(2x＋2)，得2x＋2－(x－3)＝6x ，

去括号，得2x＋2－x＋3＝6x，

移项，得6x－2x＋x＝2＋3，

合并同类项，得5x＝5，

系数化为1，得x＝1.

检验：当x＝1时，2x＋2≠0，

∴x＝1是原分式方程的解．

10. 解：设每件产品的实际定价是x元，则原定价为(x＋40)元．

根据题意，可列方程为

＝，

解得x＝160.

经检验，x＝160是原分式方程的解，且符合题意．

答：每件产品的实际定价为160元．

满分冲关

1. B　【解析】去分母，得x－2(x－1)＝－k，解得x＝k＋2.∴∴k＞－2且k≠－1.故选B.

2. 解：(1)设乙工程队单独完成这项工程需x天，依题意得

＋(＋)＝1，

解得x＝60.

经检验，x＝60是原分式方程的解，且符合题意，

答：乙工程队单独完成这项工程需60天；

(2)1÷(＋)＝24，

答：两队合作完成这项工程需24天．

3. 解：(1)设二月份每辆车售价是x元，则一月份每辆车售价是(x＋100)元，根据题意得

＝，

解得x＝900.

当x＝900时，x(x＋100)≠0，

∴x＝900是原分式方程的解，且符合题意．

答：二月份每辆车售价是900元；

(2)设每辆山地自行车的进价是y元，根据题意得

900×(1－10%)－y＝35%y，

解得y＝600.

答：每辆山地自行车的进价是600元．

核心素养提升

1. B

2. A　【解析】根据题意，得x⊗(2x－1)＝－＝1，解得x＝1.经检验，x＝1是原分式方程的解．