






广东2020中考数学一轮抢分 1.第一节 尺规作图 课件
展开第七章 图形的变化
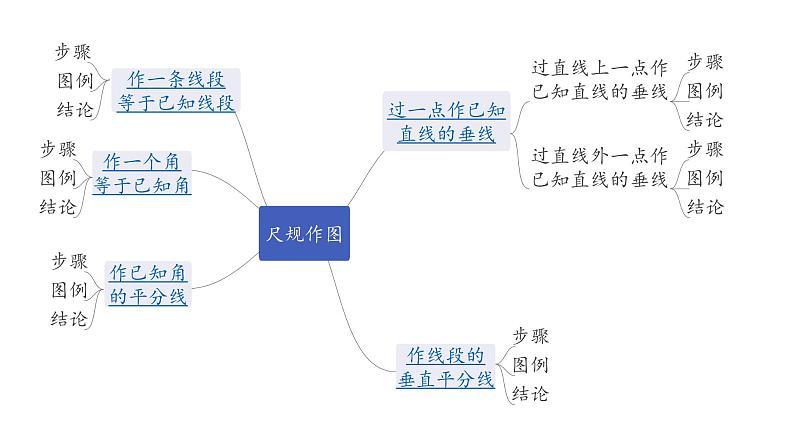
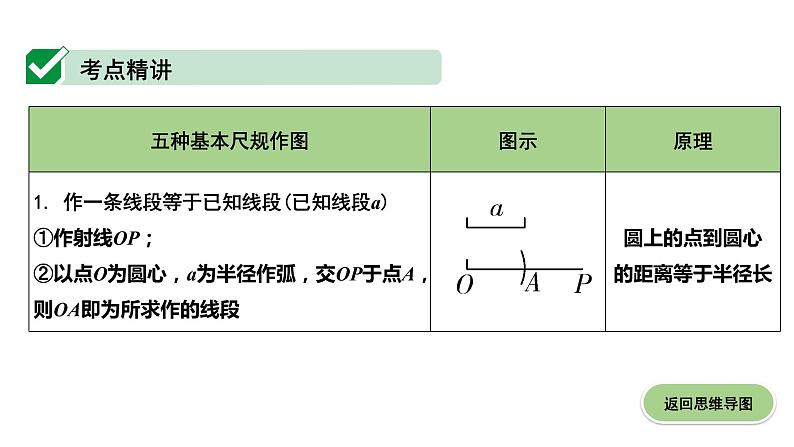
第一节 尺规作图
(建议时间: 分钟)
基础过关
1. (2019宜昌)通过如下尺规作图,能确定点D是BC边中点的是( )
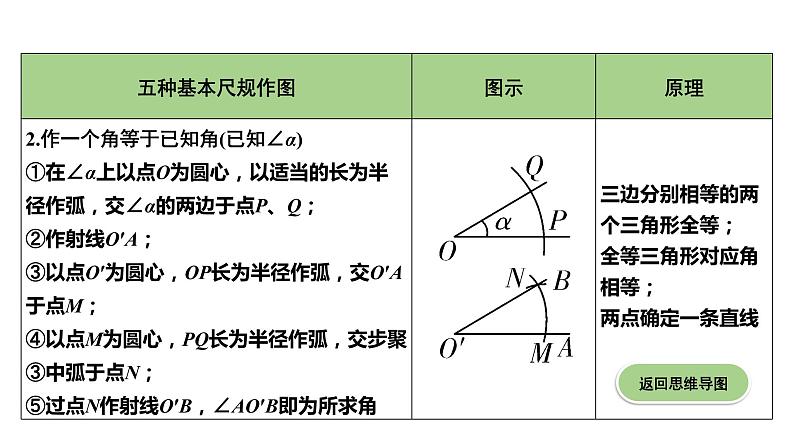
2. 如图是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是( )
A. SAS B. SSS C. AAS D. ASA
第2题图
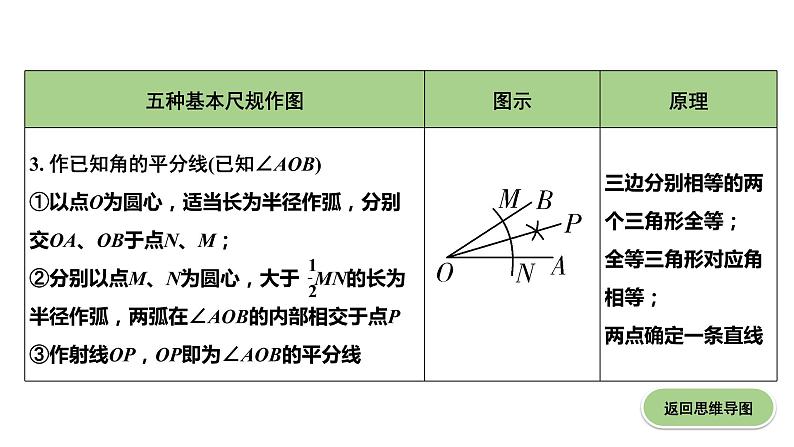
3. (2019潍坊)如图,已知∠AOB.按照以下步骤作图:
①以点O为圆心,以适当的长为半径作弧,分别交∠AOB的两边于C,D两点,连接CD;
②分别以点C,D为圆心,以大于线段OC的长为半径作弧,两弧在∠AOB内交于点E,连接CE,DE;
③连接OE交CD于点M.
下列结论中错误的是( )
- ∠CEO=∠DEO B. CM=MD C. ∠OCD=∠ECD D. S四边形OCED=CD·OE
第3题图
4. (2019成都)如图 ,▱ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO,AB于点M,N;②以点O为圆心,以AM长为半径作弧,交OC于点M′;③以点M′为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点N′;④过点N′作射线ON′交BC于点E.若AB=8,则线段OE的长为________.
第4题图
- 如图,OP平分∠MON,A是边OM上一点,以点A为圆心,大于点A到ON的距离为半径作弧,交ON于点B、C,再分别以点B、C为圆心,大于BC的长为半径作弧,两弧交于点D,作直线AD分别交OP、ON于点E、F,若∠MON=60°,EF=1,则OA=________.
第5题图
- (2019葫芦岛)如图,BD是▱ABCD的对角线,按以下步骤作图:①分别以点B和点D为圆心,大于BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则▱ABCD的边BC上的高为________.
第6题图
7. 如图,已知正方形ABCD,点E是BC边上的一点,连接DE.
(1)请用尺规作图法,在CD的延长线上截取线段DF,使DF=CE;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,连接AF. 求证:△AFD≌△DEC.
第7题图
8. (2019泰州)如图,△ABC中,∠C=90°,AC=4,BC=8.
(1)用直尺和圆规作AB的垂直平分线;(保留作图痕迹,不要求写作法)
(2)若(1)中所作的垂直平分线交BC于点D,求BD的长.
第8题图
满分冲关
1. 如图,在▱ABCD中,AD>AB.
(1)请用尺规作图法,作∠BAD的平分线交BC于点E,并在AD边上截取AF=AB,连接EF;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,判断四边形ABEF的形状,并说明理由.
第1题图
2. (2019佛山模拟)如图,△ABC中,AC=8,BC=10,AC>AB.
(1)用尺规作图法在△ABC内求作一点D,使点D到两点A、C的距离相等,又到边AC、BC的距离相等;(保留作图痕迹,不写作法)
(2)若△ACD的周长为18,求△BCD的面积.
第2题图
核心素养提升
1. (2019河北)根据圆规作图的痕迹,可用直尺成功找到三角形外心的是( )
参考答案
第一节 尺规作图
基础过关
1. A 2. B
3. C 【解析】由作图过程可知OC=OD,OE是∠AOB的平分线,∴OE是CD的垂直平分线,即CM=MD,OE⊥CD,∴CE=DE,∠MCE=∠MDE.∵∠CEO=90°-∠MCE,∠DEO=90°-∠MDE,∴∠CEO=∠DEO.选项A、B正确;∵CE>OC,∴∠COE>∠CEO,∴90°-∠COE<90°-∠CEO,即∠OCD<∠ECD,C错误;∵OE⊥CD,∴S四边形OCED=CD·OE,D正确.
4. 4 【解析】∵四边形ABCD是平行四边形,AC与BD相交于点O,∴OC=OA,由作图可知,∠COE=∠CAB,∴OE∥AB,∴OE是△CAB的中位线,∴OE=AB=4.
5. 2 【解析】由作图痕迹可知AD⊥ON,∵∠MON=60°,∴∠OAD=30°.∵∠PON=∠MON=30°,∴OF==.在Rt△AOF中,OA=2OF=2.
6. 【解析】由作图方法可知MN为BD的垂直平分线,∵四边形ABCD为平行四边形,∴四边形MBND为菱形.如解图,设BD与MN交点为点O,过点M作MG⊥BC于点G,∵BD=8,MN=6,∴OB=4,OM=3.∴MB=BN==5.∴BD·MN=BN·MG,即×8×6=5MG,解得MG=.即▱ABCD的边BC上的高为.
第6题解图
7. (1)解:如解图,DF即为所求;
第7题解图
(2)证明:在正方形ABCD中,AD=CD,∠C=∠ADC=90°,
∴∠ADF=180°-∠ADC=90°.
∴∠ADF=∠C=90°.
又∵ DF=CE,
∴△AFD≌△DEC(SAS).
8. (1)如解图,直线MN即为所求;
第8题解图
(2)如解图,连接AD,则AD=BD,
设BD=AD=x,则CD=8-x,
在Rt△ACD中,∵AC2+CD2=AD2,
∴42+(8-x)2=x2.
解得x=5,
即BD=5.
满分冲关
1. 解:(1)如解图,即为所求;
第1题解图
(2)四边形ABEF是菱形;
理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠BAE=∠DAE.
∴∠BAE=∠AEB.
∴BE=AB.
由(1)得AF=AB,
∴BE=AF.
又∵BE∥AF,
∴四边形ABEF是平行四边形.
∵AF=AB,
∴四边形ABEF是菱形.
2. 解:(1)如解图,点D即为所求;
第2题解图
(2)如解图,过点D作DF⊥BC于点F,连接AD,BD.
∵AC+CD+AD=18,DC=DA,AC=8,
∴CD=5,CE=4.
∴DE==3.
∵CD平分∠ACB,DE⊥AC,DF⊥CB,
∴DF=DE=3.
∴S△BCD=BC·DF=×10×3=15.
核心素养提升
1. C








