

















































福建2020中考数学一轮培优 第六章 圆 试卷练习课件
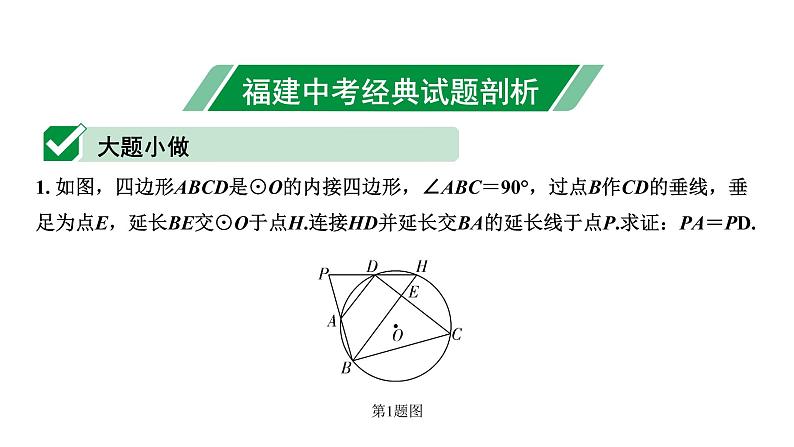
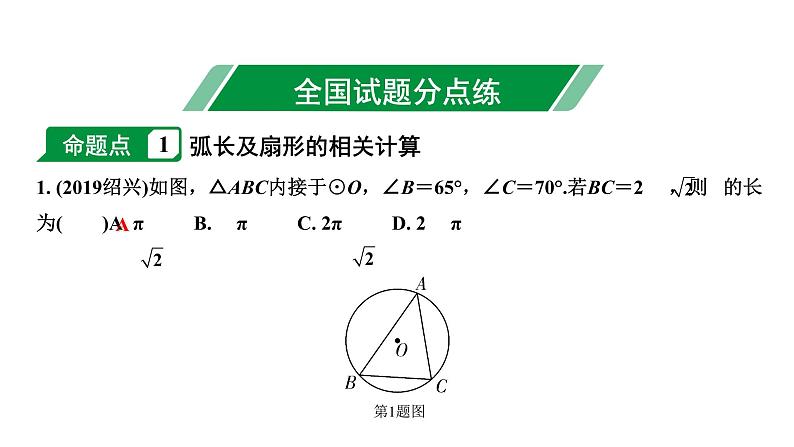
展开第六章 圆
第二节 与圆有关的位置关系
中考试题中的核心素养
数学核心素养提升
1. 在公园的O处附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均相等),现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为( )
A. E,F,G B. F,G,H
C. G,H,E D. H,E,F
第1题图
数学文化专练
《割圆术》
2. 我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度,祖冲之继承并发展了“割圆术”,将π的值精确到小数点后第七位,这一结果领先世界一千多年,“割圆术”的第一步是计算半径为1的圆内接正六边形的面积S6,则S6的值为( )
A. B. 2 C. D.
《九章算术》——勾股容圆
3. 《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步.问该直角三角形内切圆的直径是多少步.”该问题的答案是________步.
参考答案
中考试题中的核心素养
1. A 【解析】设图中小正方形的边长为x,则OA=x,OE=OF=2x,OG=x,OH=2x,∵OE=OF<OA,OG<OA,OH>OA,∴点E、F、G在⊙O内,点H在⊙O外,因此E、F、G三棵树需要被移除,故选A.
2. C 【解析】如解图,∵⊙O是单位圆,∴OA=1,∵六边形ABCDEF是正六边形,∴△OAB是正三角形,∴AB=1,过点O作OG⊥AB于点G,∴OG=OA·sin60°=,∴正六边形的面积为6S△OAB=6××AB·OG=.
第2题解图
3. 6 【解析】由勾股定理得,斜边==17.如解图,⊙O是△ABC的内切圆,AB=8,BC=15,AC=17,设⊙O的半径为r,则BE=OE=OF=BF=OG=r,AE=AG,CG=CF,∴GC=AC-AG=AC-(AB-r),FC=BC-BF=BC-r,即15-r=17-(8-r),解得2r=15+8-17=6,即直角三角形的内切圆直径是6.
第3题解图








