考点10 点、直线、平面之间的关系压轴题汇总-2020-2021学年高一《新题速递·数学》（人教版）

考点10 点、直线、平面之间的关系压轴题汇总
一、单选题（共15小题）

1.（2020秋•西城区校级期中）在三棱锥A﹣BCD中，若AD⊥BC，AD⊥BD，那么必有（　　）

A．平面ADC⊥平面BCD B．平面ABC⊥平面BCD
C．平面ABD⊥平面ADC D．平面ABD⊥平面ABC

【解答】解：在三棱锥A﹣BCD中，若AD⊥BC，AD⊥BD，且BC∩BD＝B，
可得AD⊥平面BCD，
由AD⊂平面ABD，可得平面ABD⊥平面BCD，
由AD⊂平面ACD，可得平面ACD⊥平面BCD，故A正确；
若平面ABC⊥平面BCD，又平面ACD⊥平面BCD，AC＝平面ABC∩平面ACD，
可得AC⊥平面BCD，AC⊥CD，与AD⊥CD矛盾，故B错误；
若平面ACD⊥平面ABD，又平面ABD⊥平面BCD，可得CD⊥平面ABD，CD⊥BD，不一定成立，故C错误；
若平面ABD⊥平面ABC，又平面ABD⊥平面BCD，可得BC⊥平面ABD，则BC⊥BD，不一定成立，故D错误．
故选：A．
【知识点】平面与平面垂直

2.（2020•道里区校级模拟）正方体ABCD﹣A1B1C1D1的棱长为2，E是棱DD1的中点，则平面AC1E截该正方体所得的截面面积为（　　）
A．5 B．2 C．4 D．2

【解答】解：如图所示，设 F 为 BB1的中点，
连接 AF，FC1，设 G 为 CC1的中点，
连接 EG，GB，
由EG∥AB 且 EG＝AB，得ABGE 是平行四边形，
则AE∥BG 且 AE＝BG，
又BG∥C1F 且 BG＝C1F，得AE∥C1F 且 AE＝C1F，
则A，E，C1，F 共面，
故平面AC1E 截该正方体所得的截面为 AFC1E．
又AF＝FC1＝EC1＝EA，
，EF⊥AC1，
故AFC1E 的面积为．
故选：D．

【知识点】平面的基本性质及推论

3.（2020•浙江模拟）如图，在三棱锥S﹣ABC中，SA⊥平面ABC，AB＝BC＝4，∠ABC＝90°，侧棱SB与平面ABC所成的角为45°，M为AC的中点，N是侧棱SC上一动点，当△BMN的面积最小时，异面直线SB与MN所成角的余弦值为（　　）

A． B． C． D．

【解答】解：由题意知△ABC为等腰直角三角形
，
因为M为AC的中点，所以BM⊥AC．
又SA⊥平面ABC，所以SA⊥BM，所以BM⊥平面SAC，所以BM⊥MN，
故△BMN的面积．
由题意知，所以，所以，
当MN最小时，△BMN的面积最小，此时MN⊥SC．
当MN⊥SC时，过S作SE⊥SC，交CA的延长线于点E，则SE∥MN，
连接BE，则∠BSE为异面直线SB与MN所成的角或其补角．
因为SA⊥平面ABC，所以∠SBA为直线SB与平面ABC所成的角，
所以∠SBA＝45°，所以SA＝AB＝4，所以，．
又，所以，所以，，
在Rt△EMB中，由题意知，
所以由余弦定理得：
＝＝，
故当△BMN的面积最小时，异面直线SB与MN所成角的余弦值为．
故选：D．
【知识点】异面直线及其所成的角

4.（2020秋•洛阳期中）如图，△ABC为等边三角形，D，E，F分别为AB，AC，BC的中点，AF∩DE＝G，以DE为折痕把△ADE折起，使点A到达点A'的位置，下列命题中，错误的是（　　）

A．动点A'在平面ABC上的射影在线段AF上
B．恒有平面A'GF⊥平面BCDE
C．三棱锥A'﹣EFD的体积有最大值
D．异面直线A'E与BD不可能垂直

【解答】解在等边三角形ABC中，AG⊥DE，FG⊥DE，
由A'G⊥DE，FG⊥DE，且A'G∩FG＝G，
可得DE⊥平面A'FG，
而DE⊂平面BCED，
则平面A'GF⊥平面BCED，
过A'在平面A'FG内，作A'H⊥平面ABC，
由面面垂直的性质可得A'在平面ABC上的射影在线段AF上，
故A，B正确；
又VA'﹣EFD＝A'H•S△EFD，由于S△EFD为定值，
当A'H＝A'G时，三棱锥A'﹣EFD的体积有最大值，故C正确；
在△ABC中，EF∥AB，可得异面直线A'E与BD所成角为∠A'EF（或补角），
设等边三角形ABC的边长为2，若∠A'EF＝90°，则A'E＝FE＝1，A'F＝，
由A'G＝FG＝，A'F＝，可得△A'FG存在，故D不正确．
故选：D．

【知识点】平面与平面垂直

5.（2020•道里区校级模拟）正方体ABCD﹣A1B1C1D1的棱长为2，E是棱B1C1的中点，则平面AD1E截该正方体所得的截面面积为（　　）
A．4 B．2 C．4 D．

【解答】解：取BB1中点F，连结EF、AF，
则EF∥AD1，∴梯形AFED1是平面AD1E截该正方体所得的截面，
∵正方体ABCD﹣A1B1C1D1的棱长为2，E是棱B1C1的中点，
∴AD1＝＝2，EF＝＝，
AF＝D1E＝＝，
梯形AFED1的高h＝＝，
∴平面AD1E截该正方体所得的截面面积为：
S＝（2）×＝．
故选：D．

【知识点】平面的基本性质及推论、棱柱的结构特征

6.（2020秋•万州区校级期中）在边长为a菱形ABCD中，∠DAB＝60°，将这个菱形沿对角线BD折起，使得平面DAB⊥平面BDC，若此时三棱锥A﹣BCD的外接球的表面积为5π，则a＝（　　）
A． B． C． D．3

【解答】解：取BD的中点H，连接AH，CH，
在等边三角形ABD中，AH＝a，
在等边三角形CBD中，CH＝a，
由平面DAB⊥平面BDC，AH⊥BD，平面ABD∩平面CBD＝BD，
可得AH⊥平面CBD，即有AH⊥CH，
△ACH为等腰直角三角形，
设三棱锥A﹣BCD的外接球的球心为O，半径设为R，
底面BCD的中心为O'，
在直角三角形ACH中，OC＝R＝＝＝a，
而4πR2＝5π，解得R＝，
则a＝，解得a＝，
故选：B．

【知识点】平面与平面之间的位置关系

7.（2020•江西模拟）在长方体ABCD﹣A1B1C1D1中，AD＝，AB＝，AA1＝1，过点B作直线1与直线A1D及直线AC1所成的角均为，这样的直线1的条数为（　　）
A．1 B．2 C．3 D．4

【解答】解：＝﹣，＝++，
则•＝（﹣）•（++）
＝•+2﹣•﹣2＝0+7﹣0﹣1＝6，
而||＝＝2，||＝＝3，
所以cos＜，＞＝＝，
所以直线A1D和直线AC1所成的角为，
将直线l、直线A1D和直线AC1平移至点P，
则当三条直线在同一平面时，直线l为角平分线；
若三条直线不在同一平面，则这样的直线有两条．
故这样的直线条数为3．
故选：C．

【知识点】空间中直线与直线之间的位置关系

8.（2020•河南模拟）在三棱锥P﹣ABC中，平面PBC⊥平面ABC，∠ACB＝90°，BC＝PC＝2，若AC＝PB，则三棱锥P﹣ABC体积的最大值为（　　）
A． B． C． D．

【解答】解：如图，取PB中点M，连结CM，
∵平面PBC⊥平面ABC，平面PBC∩平面ABC＝BC，
AC⊂平面ABC，AC⊥BC，
∴AC⊥平面PBC，
设点A到平面PBC的距离为h＝AC＝2x，
∵PC＝BC＝2，PB＝2x，（0＜x＜2），M为PB的中点，
∴CM⊥PB，CM＝，
解得＝，
VA﹣PBC＝＝，
设t＝，（0＜t＜2），则x2＝4﹣t2，
∴VA﹣PBC＝＝，（0＜t＜2），
关于t求导，得，令V′（t）＝0，解得t＝或t＝﹣（舍），
由V（t）单调性得当t＝时，（VA﹣PBC）max＝．
故选：D．

【知识点】棱柱、棱锥、棱台的体积、平面与平面垂直

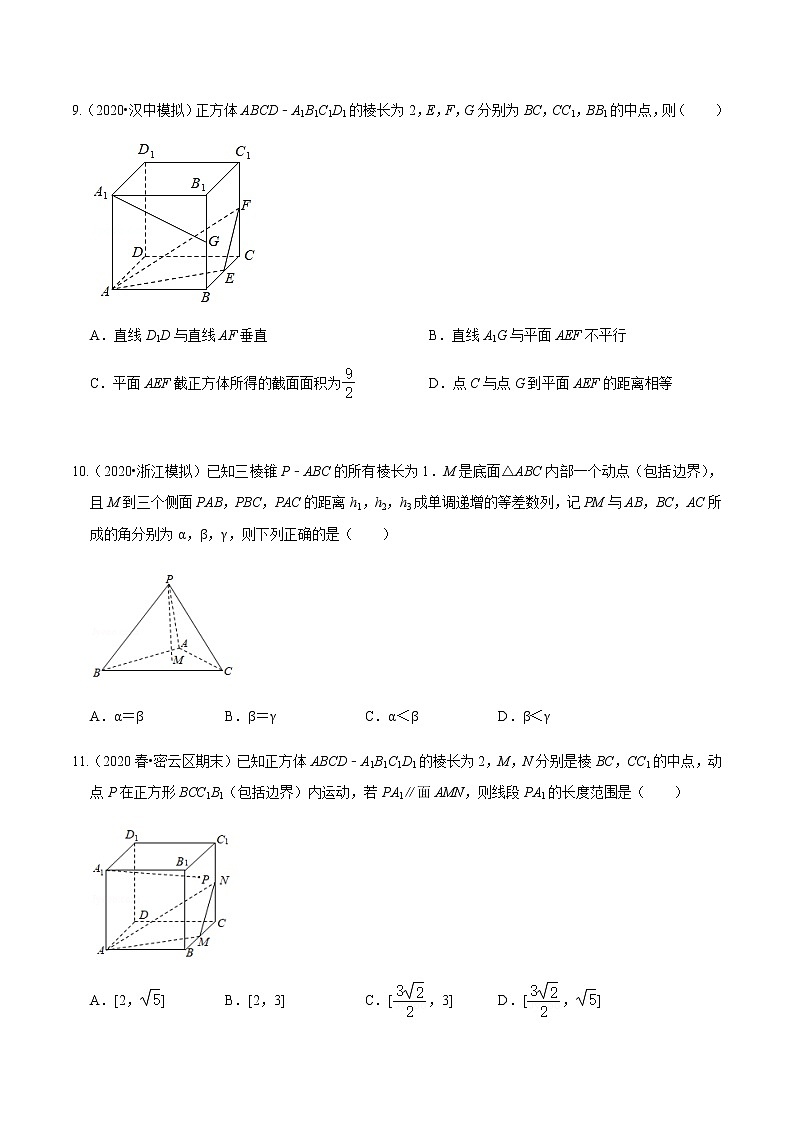
9.（2020•汉中模拟）正方体ABCD﹣A1B1C1D1的棱长为2，E，F，G分别为BC，CC1，BB1的中点，则（　　）

A．直线D1D与直线AF垂直
B．直线A1G与平面AEF不平行
C．平面AEF截正方体所得的截面面积为
D．点C与点G到平面AEF的距离相等

【解答】解：在A中，若D1D⊥AF，
又因为D1D⊥AE且AE∩AF＝A，所以DD1⊥平面AEF，
所以DD1⊥EF，所以CC1⊥EF，不成立，故A错误；
在B中，如图所示，取B1C1的中点Q，连接A1Q，GQ，
由条件可知：GQ∥EF，A1Q∥AE，且GQ∩A1Q＝Q，EF∩AE＝E，
所以平面A1GQ∥平面AEF，
又因为A1G⊂平面A1GQ，所以A1G∥平面AEF，故B错误；
在C中，如图所示，连接D1F，D1A，延长D1F，AE交于点S，
因为E，F为BC、C1C的中点，
所以EF∥AD1，所以A，E，F，D1四点共面，
所以截面即为梯形AEFD1，
又因为，，
所以，所以，故C正确；
在D中，记点C与点G到平面AEF的距离分别为h1，h2，
因为，
又因为，
所以h1≠h2，故D错误．
故选：C．


【知识点】空间中直线与直线之间的位置关系、空间中直线与平面之间的位置关系、平面的基本性质及推论

10.（2020•浙江模拟）已知三棱锥P﹣ABC的所有棱长为1．M是底面△ABC内部一个动点（包括边界），且M到三个侧面PAB，PBC，PAC的距离h1，h2，h3成单调递增的等差数列，记PM与AB，BC，AC所成的角分别为α，β，γ，则下列正确的是（　　）

A．α＝β B．β＝γ C．α＜β D．β＜γ

【解答】解：依题意知正四面体P﹣ABC的顶点P在底面ABC的射影是正三角形ABC的中心O，
由余弦定理可知，
cosα＝cos∠PMO•cos＜MO，AB＞，其中＜MO，AB＞表示直线MO与AB的夹角，
同理可以将β，γ转化，
cosβ＝cos∠PMO•cos＜MO，BC＞，其中＜MO，BC＞表示直线MO与BC的夹角，
cosγ＝cos∠PMO•cos＜MO，AC＞，其中＜MO，AC＞表示直线MO与AC的夹角，
由于∠PMO是公共的，因此题意即比较OM与AB，BC，AC夹角的大小，
设M到AB，BC，AC的距离为d1，d2，d3 则d1＝，其中θ是正四面体相邻两个面所成角，sinθ＝，
所以d1，d2，d3成单调递增的等差数列，然后在△ABC中解决问题
由于d1＜d2＜d3，可知M在如图阴影区域（不包括边界）
从图中可以看出，OM与BC所成角小于OM与AC所成角，所以β＜γ，
故选：D．

【知识点】异面直线及其所成的角

11.（2020春•密云区期末）已知正方体ABCD﹣A1B1C1D1的棱长为2，M，N分别是棱BC，CC1的中点，动点P在正方形BCC1B1（包括边界）内运动，若PA1∥面AMN，则线段PA1的长度范围是（　　）

A．[2，] B．[2，3] C．[，3] D．[，]

【解答】解：取B1C1的中点E，BB1的中点F，连结A1E，A1F，EF，取EF中点O，连结A1
∵点M，N分别是棱长为2的正方体ABCD﹣A1B1C1D1中棱BC，CC1的中点，
∴AM∥A1E，MN∥EF，
∵AM∩MN＝M，A1E∩EF＝E，
∴平面AMN∥平面A1EF，
∵动点P在正方形BCC1B1（包括边界）内运动，且PA1∥面AMN，
∴点P的轨迹是线段EF，
∵A1E＝A1F＝，EF＝，
∴A1O⊥EF，
∴当P与O重合时，PA1的长度取最小值为A1O＝，
当P与E（或F）重合时，PA1的长度取最大值为A1E＝A1F＝．
∴PA1的长度范围为[，]．
故选：D．

【知识点】直线与平面平行

12.（2020•上海）在棱长为10的正方体ABCD﹣A1B1C1D1中，P为左侧面ADD1A1上一点，已知点P到A1D1的距离为3，P到AA1的距离为2，则过点P且与A1C平行的直线交正方体于P、Q两点，则Q点所在的平面是（　　）

A．AA1B1B B．BB1C1C C．CC1D1D D．ABCD

【解答】解：如图，

由点P到A1D1的距离为3，P到AA1的距离为2，
可得P在△AA1D内，过P作EF∥A1D，且EF∩AA1于E，EF∩AD于F，
在平面ABCD中，过F作FG∥CD，交BC于G，则平面EFG∥平面A1DC．
连接AC，交FG于M，连接EM，
∵平面EFG∥平面A1DC，平面A1AC∩平面A1DC＝A1C，平面A1AC∩平面EFM＝EM，
∴EM∥A1C．
在△EFM中，过P作PQ∥EM，且PQ∩FM于Q，则PQ∥A1C．
∵线段FM在四边形ABCD内，Q在线段FM上，∴Q在四边形ABCD内．
∴则Q点所在的平面是平面ABCD．
故选：D．
【知识点】空间中直线与直线之间的位置关系

13.（2020•河南二模）如图是棱长为2的正方体ABCD﹣A1B1C1D1木块的直观图，其中P，Q，F分别是D1C1，BC，AB的中点，平面α过点D且平行于平面PQF，则该木块在平面α内的正投影面积是（　　）

A． B． C． D．

【解答】解：根据题意可知平面α过点D且平行于平面PQF，
则平面α可以平移至平面A1BC1，
木块在平面α内的正投影即可看成是在平面A1BC1的正投影，
根据投影的性质可得投影为正六边形，如图所示，
因为正方体ABCD﹣A1B1C1D1棱长为2，所以，
则投影面内正六边形的边长为：
根据正六边形面积公式可得投影的面积为：
，
故投影面积为：．
故选：A．

【知识点】直线与平面垂直、平行投影及平行投影作图法

14.（2020春•顺义区期末）如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，P为线段A1B上的动点（不含端点），则下列结论错误的是（　　）

A．平面CBP⊥平面BB1P
B．DC1⊥PC
C．三棱锥C1﹣D1PC的体积为定值
D．∠APD1的取值范围是（0，]

【解答】解：对于A，∵CB⊥BB1，CB⊥BP，BB1∩BP＝B，
∴CB⊥平面BB1P，
又CB⊂平面CBP，∴平面CBP⊥平面BB1P，故A正确；
对于B，∵DC1⊥D1C，DC1⊥BC，D1C∩BC＝C，
∴DC1⊥平面BCD1A1，又PC⊂平面BCD1A1，∴DC1⊥PC，故B正确；
对于C，∵△D1C1C的面积是定值S＝＝，
点P到平面D1C1C的距离是定值BC＝1，
∴三棱锥C1﹣D1PC的体积为定值V＝＝，故C正确；
对于D，当P与B重合时，∠APD1取最小值，
∵A1B＝，BD1＝，∴cos∠A1BD1＝＝．
∴∠APD1的最小值为arccos．
当P与A1重合时，∠APD1取最大值
∴∠APD1的取值范围是（arccos，]，故D错误．
故选：D．
【知识点】平面与平面垂直、棱柱、棱锥、棱台的体积

15.（2020•香坊区校级一模）如图，三棱锥S﹣ABC中，平面SAC⊥平面ABC，过点B且与AC平行的平面α分别与棱SA、SC交于E，F，若，则下列结论正确的序号为（　　）
①AC∥EF；
②若E，F分别为SA，SC的中点，则四棱锥B﹣AEFC的体积为；
③若E，F分别为SA，SC的中点，则BF与SA所成角的余弦值为；
④SC⊥BE．

A．②③ B．①②④ C．①②③ D．①②

【解答】解：①∵AC∥平面BEF，平面SAC∩平面BEF＝EF，AC⊂平面SAC，
∴AC∥EF，即①正确；
②取AC的中点M，连接BM、SM，
∵BA＝BC，∴BM⊥AM，
又平面SAC⊥平面ABC，平面SAC∩平面ABC＝AC，BM⊂平面ABC，
∴BM⊥平面SAC，即点B到平面AEFC的距离为BM＝．
∵SA＝SC＝2，AC＝，∴△SAC为等腰直角三角形，
∴SAEFC＝S△SAC﹣S△SEF＝SA•SC﹣SE•SF＝．
∴VB﹣AEFC＝BM•SAEFC＝××＝，即②正确；

③连接MF，
∵M、F分别为AC、SC的中点，∴FM∥SA，FM＝SA＝1，∴∠BFM即为BF与SA所成角．
在Rt△BMF中，tan∠BFM＝＝＝，
∴cos∠BFM＝，
∴BF与SA所成角的余弦值为，即③正确；
④连接EM，
由②知，BM⊥平面SAC，∴BM⊥SC，
若SC⊥BE，∵BM∩BE＝B，BM、BE⊂平面BME，∴SC⊥平面BME，
又EM⊂平面BME，∴SC⊥EM，这与SC∥EM相矛盾，即④错误．
∴正确的有①②③，
故选：C．
【知识点】异面直线及其所成的角、棱柱、棱锥、棱台的体积


二、填空题（共10小题）

16.（2020•韶关二模）已知长方体ABCD﹣A1B1C1D1中，AB＝3，AD＝4，AA1＝10，E，F，M分别是棱AB，BC，CC1的中点，P是该长方体底面ABCD上的动点，若PD1∥平面EFM，则△PBB1面积的取值范围是　　．

【解答】解：补全截面EFM为截面EFMHQR如图，设BR⊥AC，
∵直线D1P与平面EFM不存在公共点，
∴D1P∥平面EFMHQR，
易知平面ACD1∥平面EFMHQR，
∴P∈AC，
且当P与R重合时，BP＝BR最短，此时△PBB1的面积最小；
由等积法：BR×AB×BC，
即：BR×＝×3×4；
∴BP＝，
又BB1⊥平面ABCD，∴BB1⊥BP，△PBB1为直角三角形，
∴△PBB1的面积为：××10＝12，
当P与C重合时，PB＝BC最长为4，此时△PBB1的面积最大；
最大值为：×4×10＝20；
故答案为：[12，20]．

【知识点】直线与平面平行

17.（2020•南昌二模）已知四棱锥P﹣ABCD的底面ABCD是边长为3的正方形，PD⊥平面ABCD，PD＝6，E为PD中点，过EB作平面α分别与线段PA、PC交于点M，N，且AC∥α，则＝　　，四边形EMBN的面积为　　．

【解答】解：延伸平面α，交AC所在的平面ABCD于RS，
即平面α∩平面ABCD＝RS，
又B∈平面α∩平面ABCD，
∴B∈RS，即R，S，B三点共线，
又AC∥α，
由线面平行的性质定理可得AC∥RS，
则∠ARB＝∠ABR＝，即AR＝AB，
∴点A为RD的中点，E为PD中点，
则PD＝RD＝6，DA＝DE＝3，∠PDA＝∠ADP＝，
∴△PAD≌△RED，
∴∠MPE＝∠MRA，又∠PME＝∠RMA，PE＝RA，
∴△PME≌△RMA，则ME＝MA，
过M作MK⊥PD，交PD于点K，
∴•＝2•＝2•，则PM＝2MA，
∴，
∴MN＝＝2，
∵AC⊥BD，AC⊥PD，BD∩PD＝D，
∴AC⊥平面PBD，
∴MN⊥平面PBD，
∴MN⊥BE，
∴四边形EMBN的面积为S＝＝＝3．
故答案为：；．

【知识点】直线与平面平行

18.（2020春•湖北期末）如图所示，在四棱锥P﹣ABCD中，PA⊥平面ABCD，PC⊥AD，底面ABCD为梯形，AB∥DC，AB⊥BC，AB＝BC，点E在棱PB上，若PD∥平面EAC，则＝　　．


【解答】解：如图所示，连接BD交AC于点O，连接OE，

∵PA⊥平面ABCD，AD⊂面ABCD，∴PA⊥AD，
∵PC⊥AD，PA∩PC＝P，PA、PC⊂面PAC，∴AD⊥面PAC，
∵AC⊂面PAC，∴AD⊥AC．
∵AB⊥BC，AB＝BC，∴AC＝AB，∠BAC＝45°，
又AB∥DC，∴∠ACD＝∠BAC＝45°，∴△ACD为等腰直角三角形，CD＝AC＝2AB，
∴＝＝．
∵PD∥平面EAC，PD⊂面PBD，且平面EAC∩平面PBD＝OE，
∴OE∥PD，
∴＝＝2．
故答案为：2．
【知识点】直线与平面平行

19.（2020春•驻马店期末）在正方体ABCD﹣A1B1C1D1中，E，F分别为线段A1B1，AB的中点，O为四棱锥E﹣C1D1DC的外接球的球心，点M，N分别是直线DD1，EF上的动点，记直线OC与MN所成的角为θ，则当θ最小时，tanθ＝　　．

【解答】解：如图，设P，Q分别是棱CD和C1D1的中点，
则四棱锥E﹣C1D1DC的外接球即三棱柱DFC﹣D1EC1的外接球，
∵三棱柱DFC﹣D1EC1是直三棱柱，
∴其外接球球心O为上、下底面三角形外心G和H连结的中点，
由题意，MN是平面DD1EF内的一条动直线，
记直线OC与MN所成角为θ，
则θ的最小值是直线OC与平面DD1EF所成角，
即问题转化为求直线OC与平面DD1EF所成角的正切值，
不妨设正方体ABCD﹣A1B1C1D1中棱长为2，则EQ＝2，ED1＝，
∵△EC1D1为等腰三角形，∴△EC1D1外接圆直径为2GE＝＝＝，
则GE＝，GQ＝2﹣＝＝PH，
如图，以D为原点，DA，DC，DD1所在直线为x，y，z轴，建立空间直角坐标系，
则D（0，0，0），D1（0，0，2），C（0，2，0），F（2，1，0），O（ ，1，1），
＝（0，0，2），＝（2，1，0），＝（﹣，1，﹣1），
设平面DD1EF的法向量＝（x，y，z），
则，取x＝1，得＝（1，﹣2，0），
则sinθ＝＝，tanθ＝．
∴当θ最小时，tanθ＝．
故答案为：．

【知识点】异面直线及其所成的角

20.（2020•淮北二模）已知正四棱锥P﹣ABCD的底面边长为，高为，其内切球与面PAB切于点M，球面上与P距离最近的点记为N，若平面α过点M，N且与AB平行，则平面α截该正四棱锥所得截面的面积为　　．

【解答】解：取AB，CD中点Q，R，连结PQ，PR，QR，取QR中点S，连结PS，
则RQ⊥AB，S为正方形ABCD的中心，四棱锥P﹣ABCD是正四棱锥，
∴PS⊥平面ABCD，∴PS＝6，
在Rt△PSQ中，PQ＝＝＝4，
同理，PR＝4，∴△PQR是正三角形，
∴正四棱锥P﹣ABCD内切球的球心为正△PQR的内心O，
内切球的半径是正△PQR的内切圆半径为2，
内切球与平面PAB的切点M为正△PQR内切圆与直线PQ的切点，
∴M为PQ中点，球面上与P距离最近的点为连结OP与球面的交点，
即在OP之间，且ON＝2，∴N为OP中点，
连结MN并延长交PR于I，平面α过M，N，I与直线AB平行，
设平面α分别与平面PAB，平面PCD交于EF，GH，
∵AB⊂平面PAB，∴EF∥AB，又∵AB∥CD，∴CD⊄α，
∴CD∥α，同理可证GH∥CD，∴EF∥GH，连结GF，HE，
则梯形EFGH为所求的截面，
∵RQ⊥AB，PS⊥AB，PS∩RQ＝S，∴AB⊥平面PQR，
∵IM⊂平面PQR，∴AB⊥IM，AB∥EF，∴EF⊥IM，
连结OQ，则OQ为∠POS的角平分线，∴∠PQO＝30°，
∵M，N是PQ，PO的中点，∴MN∥OQ，
∴∠PMI＝∠PQO＝30°，而∠MPI＝60°，∴∠PIM＝90°，
∴MI＝PMcos30°＝3，PI＝PMsin30°＝＝，
又HG∥CD，∴HG＝＝，
∴截面梯形EFGH的面积为S＝＝＝9．
故答案为：9．

【知识点】平面的基本性质及推论

21.（2020春•通州区期末）如图，在边长为2正方体ABCD﹣A1B1C1D1中，E为BC的中点，点P在正方体表面上移动，且满足B1P⊥D1E，则点B1和满足条件的所有点P构成的图形的面积是　　　　　　．


【解答】解：以D为坐标原点，DA所在直线为x轴，DC所在直线为y轴，DD1所在直线为z轴，
建立空间直角坐标系，如图所示；
则D1（0，0，2），E（1，2，0），B1（2，2，2），
设点P（x，y，z），则 ＝（x﹣2，y﹣2，z﹣2），＝（1，2，﹣2），
又B1P⊥D1E，∴•＝（x﹣2）+2（y﹣2）﹣2（z﹣2）＝0，
即x+2y﹣2z﹣2＝0．
又点P在正方体的表面上，
当z＝0时，x+2y﹣2＝0，是线段AM，点M（0，1，0）；
当z＝1时，x+2y﹣4＝0，是点B1（2，2，2）；
当x＝0时，2y﹣2z﹣2＝0，是线段MN，点N（0，2，1）；
当x＝1时，2y﹣2z﹣1＝0，是线段AB1；
当y＝0时，x﹣2z﹣2＝0，是点A（2，0，0）；
当y＝1时，x﹣2z＝0，是线段B1N．
如图所示，点P的轨迹构成的图形是四边形AB1NM．
∵MN∥AB1，AB1＝2，MN＝＝，
A（2，0，0），M（0，1，0），B1（2，2，2），＝（﹣2，1，0），＝（0，2，2），
∴点M到AB1的距离d＝||•＝＝，
∴点B1和满足条件的所有点P构成的图形的面积是：
＝＝．
故答案为：．

【知识点】平面的基本性质及推论、直线与平面垂直

22.（2020春•河南月考）已知四棱锥P﹣ABCD中，PA⊥平面ABCD，PA＝2，底面ABCD是边长为2的正方形，用与直线PA、BD都平行的平面截此四棱锥，截面与AB、AD、PD、PC、PB分别交于F、G、H、M、E，则截面EFGHM面积的最大值为　　　　　　．

【解答】解：设＝λ（0＜λ＜1），连接AC，BD，AC交BD，FG分别于O，N，连接NM，
∵PA⊥平面ABCD，
∴PA⊥BD，
∵PA∥平面EFGHM，
∴EF∥PA，MN∥PA，GH∥PA，
∴＝＝＝1﹣，
∴EF∥GH∥MN，
∴EF＝2（1﹣λ），
∵BD∥平面EFGHM，连接EH，
∴FG∥BD，EH∥BD，
∴＝＝＝λ，FG∥EH，＝＝＝1﹣，
∴四边形EFGH为矩形，FG＝λBD＝2λ，MN＝2﹣λ，MN⊥FG，
∴S截面EFGHM＝S矩形EFGH+S△MGH＝2（1﹣λ）×2λ+×2λ[（2﹣λ）﹣2（1﹣λ）]＝﹣3（λ﹣）2+，
当λ＝时，截面EFGHM面积的最大值为，
故答案为：．

【知识点】平面的基本性质及推论

23.（2020•长春二模）三棱锥A﹣BCD的顶点都在同一个球面上，满足BD过球心O，且BD＝2，三棱锥A﹣BCD体积的最大值为　　；三棱锥A﹣BCD体积最大时，平面ABC截球所得的截面圆的面积为　　．

【解答】解：当BD过球心，所以∠BAD＝∠BCD＝90°，
所以AO⊥面BCD，VA﹣BCD＝，当BC＝CD时体积最大，
因为BD＝2，OA＝，所以BC＝CD＝2，
所以最大体积为：＝；
三棱锥A﹣BCD体积最大时，三角形ABC中，AB＝AC＝＝2＝BC，
设三角形ABC的外接圆半径为r，则2r＝，所以r＝，
所以外接圆的面积为S＝πr2＝，
故答案分别为：，．

【知识点】平面的基本性质及推论

24.（2020•淇滨区校级模拟）已知P，A，B，C，D是球O的球面上的五个点，四边形ABCD为梯形，AD∥BC，AB＝DC＝AD＝2，BC＝4，△PAD为等边三角形且平面PAD⊥平面ABCD，则球O的表面积为　　．

【解答】解：由题意可知，几何体的图形，如图：△PAD为等边三角形，F为AD的中点，
底面ABCD是等腰梯形，侧面PAD是正三角形与底面ABCD垂直，所以四棱锥的外接球的球心是O，在底面ABCD的外心E的垂直直线与侧面PAD的外心G的垂直直线的交点，
因为AD∥BC，AB＝DC＝AD＝2，BC＝4，△PAD为等边三角形且平面PAD⊥平面ABCD，
所以E是底面ABCD的外心，半径为2，OE＝GF，G是正三角形的外心，OE＝，EA＝2，
所以外接球的半径为R＝＝，
则球O的表面积为：4π×＝．
故答案为：．

【知识点】平面与平面垂直、球的体积和表面积

25.（2020•邯山区校级模拟）如图，正方形ABCD﹣A1B1C1D1的棱长为，动点P在对角线BD1上，过点P作垂直于BD1的平面，记这样得到的截面多边形（含三角形）的面积为y，设BP＝x，则当x∈[1，5]时，函数y＝f（x）的值域为　　．


【解答】如图：∵正方形ABCD﹣A1B1C1D1的棱长为，
∴正方体的对角线长为6，
∵x∈[1，5]，根据对称性可得：当x＝1或5时，三角形的面积最小，
设截面三角形的边长为t，由等体积法得：，
∴，∴．
当x＝3，即P在BD1中点时，截面为正六边形的面积最大，
此时正六边形的边长为，故截面面积为．
故答案为：．

【知识点】平面的基本性质及推论


三、解答题（共10小题）

26.（2020秋•洛阳月考）如图，在三棱柱ABC﹣A1B1C1中，侧面AA1C1C⊥底面ABC，∠C1CA＝60°，AB⊥AC，AC＝AB＝AA1＝2．
（1）求证：CA1⊥BC1；
（2）求三棱柱ABC﹣A1B1C1的侧面积．


【解答】解：（1）∵AC＝AA1，∴侧面ACC1A1是菱形，∴AC1⊥CA1．
∵侧面AA1C1C⊥底面ABC，且平面ABC∩平面AA1C1C＝AC，AB⊥AC，∴AB⊥平面AA1C1C．
又∵CA1⊂平面AA1C1C，∴CA1⊥AB．
又AC1∩AB＝A，∴CA1⊥平面C1AB．
又BC1⊂平面C1AB，∴CA1⊥BC1．
（2）设棱CA的中点为D，连C1D，BD，则C1D⊥AC，
∴C1D⊥底面ABC．从而C1D⊥BD．
由∠C1CA＝60°，AC＝AB＝AA1＝2．
得AD＝1，，
∴．
在△BCC1中，由余弦定理得，从而．
∴．
由（1）知AB⊥平面AA1C1C，∴AA1⊥AB，，
又．
∴三棱柱ABC﹣A1B1C1的侧面积为．

【知识点】棱柱、棱锥、棱台的侧面积和表面积、直线与平面垂直

27.（2020秋•潞州区校级月考）如图，在四棱锥P﹣ABCD中，底面ABCD是平行四边形，AB＝AC＝2，AD＝2，PB＝，PB⊥AC．
（1）求证：平面PAB⊥平面PAC；
（2）若∠PBA＝45°，点E在线段PA上，且三棱锥D﹣PCE的体积为，求．


【解答】（1）证明：∵AB2+AC2＝BC2，∴AB⊥AC，
又PB⊥AC，AB∩PB＝B，∴AC⊥平面PAB，
又AC⊂平面PAC，∴平面PAB⊥平面PAC，
（2）解：∵∠PBA＝45°，∴，AP2+BP2＝AB2，∴BP⊥AP，
过点P作PM⊥AB，交AB于点M，则PM＝1，
由（1）AC⊥平面PAB，且PM⊂平面PAB，AC⊥PM，且AB∩AC＝A，
∴PM⊥平面ABCD，
设点E到平面ACD的距离为h，则VD﹣PCE＝VP﹣ACD﹣VE﹣ACD
＝
＝
＝＝，
解得：，所以点E到平面ACD的距离为，
∴．

【知识点】棱柱、棱锥、棱台的体积、平面与平面垂直

28.（2020秋•上高县校级月考）如图1，C，D是以AB为直径的圆上两点，且AB＝2AD，AC＝BC，将△ABC所在的半圆沿直径AB折起，使得点C在平面ABD上的射影E在BD上，如图2．
（1）求证：BC⊥平面ACD；
（2）在线段AB上是否存在点F，使得AD∥平面CEF？若存在，求出的值；若不存在，请说明理由．


【解答】解：（1）证明：∵AB是圆的直径，
∴AD⊥BD．
∵CE⊥平面ABD，AD⊂平面ABD，
∴CE⊥AD．
又∵CE∩BD＝E，BD，CE⊂平面BCD，
∴AD⊥平面BCD．
∵BC⊂平面BCD，
∴AD⊥BC．
又∵BC⊥AC，AC∩BC＝C，
∴BC⊥平面ACD．
（2）解：连接AE，∵CE⊥平面ABD，AE，BE⊂平面ABD，
∴CE⊥AE，CE⊥BE．
在Rt△ACE和Rt△BCE中，由AC＝BC得AE＝BE，
在Rt△ABD中，由AB＝2AD，得∠ABD＝30°，
∴∠AED＝∠ABE+∠BAE＝60°，
∴在Rt△ADE中，DE＝AE，
∴E是BD的三等分点，且DE＝EB．
在线段AB上存在点F，使得AF＝FB，则有FE∥AD．
∵FE⊂平面CEF，AD⊄平面CEF，
∴AD∥平面CEF．
故在线段AB上存在点F，使得AD∥平面CEF，此时＝．

【知识点】直线与平面平行、直线与平面垂直

29.（2020秋•五华区校级月考）如图，在三棱柱ABC﹣A1B1C1中，四边形AA1C1C是边长为的正方形，CC1⊥BC，BC＝1，AB＝2．
（1）证明：平面A1BC⊥平面ABC1；
（2）在线段A1B上是否存在点M，使得CM⊥BC1，若存在，求的值；若不存在，请说明理由．


【解答】解：（1）证明：在△ABC中，AB＝2，BC＝1，AC＝，
有AC2+BC2＝AB2，可得AC⊥BC，
又CC1⊥BC，AC∩CC1＝C，可得BC⊥平面AA1C1C，
即有BC⊥AC1，
由四边形AA1C1C是边长为的正方形，可得A1C⊥AC1，
而BC∩A1C＝C，可得AC1⊥平面A1BC，
又AC1⊂平面ABC1，则平面A1BC⊥平面ABC1；
（2）在线段A1B上存在点M，使得CM⊥BC1，且＝．
理由如下：由（1）可得，以C为原点，
CA，CB，CC1所在直线分别为x，y，z轴距离空间直角坐标系，
如图所示，则A（，0，0），C（0，0，0），B（0，1，0），A1（，0，），C1（0，0，），
设M（x，y，z），＝λ，
所以（x，y﹣1，z）＝λ（，﹣1，），解得x＝λ，y＝1﹣λ，z＝λ，
所以＝（λ，1﹣λ，λ），＝（0，1，﹣），要使CM⊥BC1，
则需•＝0，即1﹣λ﹣3λ＝0，解得λ＝．
故＝．

【知识点】平面与平面垂直

30.（2020秋•梅河口市校级月考）如图，在三棱柱ABC﹣A1B1C1中，底面△ABC为直角三角形，AC⊥BC，侧棱CC1⊥底面ABC，AC＝CC1
（1）证明：平面A1BC⊥平面ABC1；
（2）若点E为侧棱AA1的中点，点F为棱BC上的一点，且BC＝3BF，证明：A1B∥平面C1EF．


【解答】证明：（1）因为侧棱CC1⊥底面ABC，且AC＝CC1，
所以四边形AA1C1C为正方形，可知AC1⊥A1C，
又BC⊥AC，由已知侧棱CC1⊥底面ABC可得CC1⊥BC，AC∩CC1＝C，
可得BC⊥平面AA1C1C，AC1⊂平面AA1C1C，
可知AC1⊥BC，BC∩A1C＝C，
又A1C，BC⊂平面ABC，
所以AC1⊥平A1BC，AC1⊂平面ABC1，
所以，平面A1BC⊥平面ABC1．
（2）如图，设A1C与C1E相交于点M，连接MF，
在正方形AA1C1C中，
由已知BC＝3BF，可得，
在△A1BC中，，则有MF∥A1B，MF⊂平面C1EF，
又A1B⊄平面C1EF，
所以A1B∥平面C1EF．

【知识点】直线与平面平行、平面与平面垂直

31.（2020秋•金台区期中）如图，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD是菱形，且AB＝AA1＝1，E是棱AA1的中点，EC＝．
（1）求证：平面EDD1⊥平面EDC；
（2）求三棱锥D1﹣DEC的体积．


【解答】解：（1）证明：∵点E是AA1的中点，∴AE＝1
∵AD＝1，∴在Rt△EAD中，DE＝，
由题意知EC＝，DC＝1，则DC2+DE2＝EC2，∴DE⊥CD，
∵四棱柱ABCD﹣A1B1C1D1是直四棱柱，∴CD⊥DD1，
∵DD1，DE⊂平面EDD1，且DD1∩DE＝D，∴CD⊥平面EDD1，
又CD⊂平面EDC，∴平面EDD1⊥平面EDC．
（2）解：由（1）可知，CD⊥平面EDD1，
∵D1E＝，ED＝，DD1＝2，
∴＝，∴D1E⊥DE，
∴三棱锥D1﹣DEC的体积为：
＝＝＝＝．

【知识点】平面与平面垂直、棱柱、棱锥、棱台的体积

32.（2020春•海淀区校级期末）如图所示，在正方体ABCD﹣A1B1C1D1中，点G在棱D1C1上，且D1G＝D1C1，点E、F、M分别是棱AA1、AB、BC的中点，P为线段B1D上一点，AB＝4．
（Ⅰ）若平面EFP交平面DCC1D1于直线l，求证：l∥A1B；
（Ⅱ）若直线B1D⊥平面EFP．
（i）求三棱锥B1﹣EFP的表面积；
（ii）试作出平面EGM与正方体ABCD﹣A1B1C1D1各个面的交线，并写出作图步骤，保留作图痕迹．设平面EGM与棱A1D1交于点Q，求三棱锥Q﹣EFP的体积．


【解答】解：（1）在正方体ABCD﹣A1B1C1D1中，
因为平面ABB1A1∥平面 DCC1D1，平面EFP∩平面 ABB1A1＝EF，
所以EF∥l，
因为点E、F 分别是棱 AA1、AB 的中点，
所以 EF∥A1B，
所以l∥A1B．
（2）（i）因为直线 B1D⊥平面 EFP，EP⊂平面 EFP，
所以 B1D⊥EP，又因为△DAE≌△B1A1E，
所以DE＝B1E，
所以DP＝B1P，
因为，
×，
，
所以三棱锥B1﹣EFP的表面积为．
（ii）作图步骤如下：
连接GE，过点G作GH⊥DC于点H，连接HA并延长交GE的延长线于点I，连接IM并延长交AB于点J交DC的延长线于点K，
再连接GK交CC1于点S，连接MS并延长交B1C1的延长线于点R，连接RG并延长交A1D1于点Q，再连接EQ，GS，EJ，
则图中EQ，QG，GS，SM，MJ，JE即为平面EGM与正方体各个面的交线．

设 BJ＝CK＝x，由题知
2AJ＝HC+CK＝3+x，
所以，所以，
解得，
因为，
∵MC＝2，∴，
所以，

如上图，设N为线段A1D1的中点，可证点N在平面PEF内，且三角形PNE与三角形PEF面积相等，
所以，三棱锥Q﹣EFP的体积＝三棱锥Q﹣ENP的体积＝三棱锥P﹣ENQ的体积＝，
所以三棱锥Q﹣EFP 的体积为 ．
【知识点】平面与平面垂直、棱柱、棱锥、棱台的体积、棱柱、棱锥、棱台的侧面积和表面积

33.（2020•南昌三模）三棱柱ABC﹣A1B1C1中，AB＝2，，AC＝2，四边形ABB1A1为菱形，且∠ABB1＝60°，AC⊥CC1．
（Ⅰ）求证：平面ABB1A1⊥平面BB1C1C；
（Ⅱ）求点B1到平面ABC的距离．


【解答】解：（Ⅰ）证明：取BB1中点O，
连接AB1，OA，OC，B1C，菱形中∠ABB1＝60°，
故三角形ABB1是等边三角形，
则AO⊥BB1，BO＝1，，
又BB1∥CC1，AC⊥CC1，
所以AC⊥BB1，又AO⊥BB1，AO∩AC＝A，
故BB1⊥平面AOC，
所以BB1⊥CO，在Rt△BOC中，，
所以CO2+AO2＝AC2，故CO⊥AO，
又AO⊥BB1，所以AO⊥平面BB1C1C，
又AO⊆平面ABB1A1，所以平面ABB1A1⊥平面BB1C1C．
（Ⅱ）解：由（1）知：，
则，
在△ABC中，，，
，
设点B1到平面ABC的距离为h，则．
故点B1到平面ABC的距离为．

【知识点】平面与平面垂直、点、线、面间的距离计算

34.（2020春•大兴区期末）如图所示，在正方体ABCD﹣A1B1C1D1中，AA1＝1．
（Ⅰ）求证：BD⊥A1C；
（Ⅱ）求证：平面BDC1⊥平面A1B1C；
（Ⅲ）用一张正方形的纸把正方体ABCD﹣A1B1C1D1完全包住，不将纸撕开，求所需纸的最小面积．（结果不要求证明）


【解答】解：（Ⅰ）证明：连结AC，在正方体ABCD﹣A1B1C1D1中，
∵底面ABCD是正方形，∴AC⊥BD，
∵AA1⊥平面ABCD，∴BD⊥AA1，
∵AA1∩AC＝A，∴BD⊥平面A1AC，
∵A1C⊂平面A1AC，∴BD⊥A1C．
（Ⅱ）证明：∵侧面BCC1B1是正方形，∴BC1⊥B1C，
∵A1B1⊥平面BCC1B1，∴A1B1⊥BC1，
∵A1B1∩B1C＝B1，∴BC1⊥平面A1B1C，
∵BC1⊂平面BDC1，∴平面BDC1⊥平面A1B1C；
（Ⅲ）用一张正方形的纸把正方体ABCD﹣A1B1C1D1完全包住，
不将纸撕开，所需纸的最小面积为8．

【知识点】平面与平面垂直、直线与平面垂直

35.（2020•丹阳市模拟）如图，在直三棱柱ABC﹣A1B1C1中，AB⊥BC，BB1＝BC，B1C∩BC1＝M，N为A1B的中点．
（1）求证：直线MN∥平面ABC；
（2）求证：BC1⊥A1C．


【解答】证明：（1）∵直三棱柱ABC﹣A1B1C1中，四边形BB1C1C和四边形AA1C1C都是平行四边形，
∴AC∥A1C1，
在▱BB1C1C中，BC1∩B1C＝M，则M为BC1中点，
∵N为A1B中点，∴MN为△A1BC1的中位线，
∴MN∥A1C1，
∵A1C1∥AC，∴MN∥AC，
∵MN⊄平面ABC，AC⊂平面ABC，
∴MN∥平面ABC．
（2）BB1⊥平面A1B1C1，BB1⊂平面B1BCC1，
∴平面B1BCC1⊥平面A1B1C1，
∵AB⊥BC，∴A1B1⊥B1C1，
∵A1B1⊂平面A1B1C1，B1C1为交线，∴A1B1⊥平面B1BCC1，
∵BC1⊂平面B1BCC1，∴A1B1⊥BC1，
∵BB1＝BC，∴侧面B1BCC1为菱形，∴B1C⊥BC1，
∵A1B1∩B1C＝B1，∴BC1⊥平面A1B1C，
∵A1C⊂平面A1B1C，∴BC1⊥A1C．

【知识点】直线与平面垂直、直线与平面平行