高中数学人教A版 (2019)选择性必修 第二册4.3 等比数列课文配套课件ppt

这是一份高中数学人教A版 (2019)选择性必修 第二册4.3 等比数列课文配套课件ppt，共43页。PPT课件主要包含了必备知识·素养奠基，amqn-m，ap·aq，等比数列的单调性，a10，关键能力·素养形成，课堂检测·素养达标等内容，欢迎下载使用。

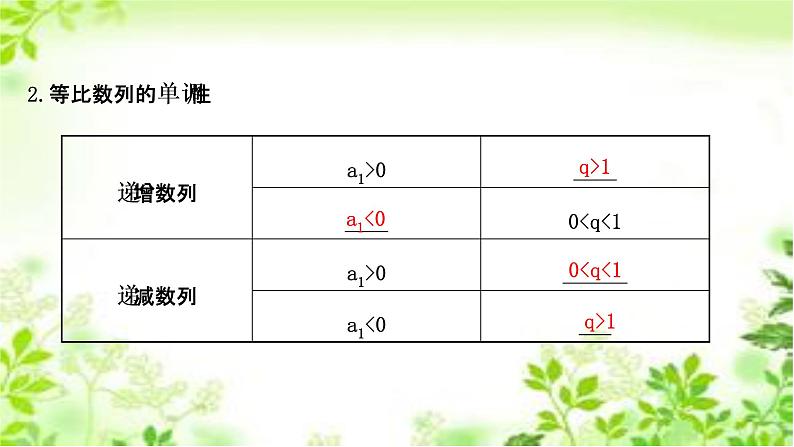
1.等比数列的项之间的关系等比数列{an},m,n,p,q∈N*
【思考】等比数列两项之间的关系an=amqn-m中,当n≤m时成立吗?提示:成立,如a2=a5q2-5=a5q-3=
【思考】当q=1,q<0时,分别是什么数列?提示:当q=1时是常数列;当q<0时是摆动数列.
【素养小测】1.思维辨析(对的打“√”,错的打“×”)(1)等比数列{an}中a2·a6= (　　)(2)当等比数列的公比q>1时,一定是递增数列.(　　)(3)等比数列{an}中,a1,a4,a7,a10,…仍然是等比数列.(　　)
提示:(1)×.a2·a6= (2)×.当数列的公比q>1时,若a1<0,则是递减数列.(3)√.a1,a4,a7,a10,…是以a1为首项,q3为公比的等比数列.
2.等比数列{an}的公比q=- ,a1= ,则数列{an}是(　　)A.递增数列B.递减数列C.常数列D.摆动数列【解析】选D.由于公比q=- <0,所以数列{an}是摆动数列.
3.在等比数列{an}中,已知a7·a12=10,则a8·a9·a10·a11=________. 【解析】因为a7·a12=a8·a11=a9·a10=10,所以a8·a9·a10·a11=102=100.答案:100
类型一　等比数列性质的应用 【典例】1.若数列{an}是递增的等比数列,a2a5=20,a1+a6=9,则a11=(　　) 2.已知各项都为正数的等比数列{an}满足:a3a7=2 ,a3=1,则a2=(　　) 【思维·引】1.利用a2a5=a1a6转化求值.2.利用a3a7= 求出q,进而求出a2.
【解析】1.选C.因为数列{an}是递增的等比数列,a2a5=20,a1+a6=9,所以a1a6=a2a5=20,所以a1,a6是一元二次方程x2-9x+20=0的两个根,且a12.选B.各项都为正数的等比数列{an}满足:a3a7=2 ,所以 =2 ,所以q= ,因为a3=1,所以a2=
【内化·悟】　用数列项的哪个要素的关系来确定所用的性质?提示:需要用数列项的下标关系,即项数的关系.
【类题·通】1.解答等比数列问题的基本方法——基本量法(1)基本步骤:运用方程思想列出基本量a1和q的方程组,解出a1和q,然后利用通项公式求解.(2)优缺点:适用面广,入手简单,思路清晰,但有时运算稍繁.
2.利用等比数列的性质解题(1)基本思路:充分发挥项的“下标”的指导作用,分析等比数列项与项之间的关系,选择恰当的性质解题.(2)优缺点:简便快捷,但是适用面窄,有一定的思维含量.
【习练·破】　(2020·眉山高二检测)已知数列{an}为正项的递增等比数列,a1+a6=12,a2a5=20,则 =(　　)A.5B.10C.25D.510
【解析】选C.设等比数列{an}的公比为q.因为数列{an}为正项的递增等比数列,a1+a6=12,a2a5=20,所以 解得a1=2,q= ,所以 =q10=25.
【加练·固】　　(2020·惠州高二检测)已知数列{an}是等比数列,函数y=x2-5x+3的两个零点是a1,a5,则a3=(　　)A.1B.-1C.± D. 【解析】选D.由根与系数的关系可知a1+a5=5,a1·a5=3,则a1>0,a5>0,从而a3>0,且 =a1·a5=3,所以a3= .
类型二　等比数列的实际应用【典例】朱载堉(1536-1611),明太祖九世孙,音乐家、数学家、天文历算家,在他多达百万字的著述中以《乐律全书》最为著名,在西方人眼中他是大百科全书式的学者王子.他对文艺的最大贡献是创建了“十二平均律”,此理论被广泛应用在世界各国的键盘乐器上,包括钢琴,故朱载堉被誉为“钢琴理论的鼻祖”.“十二平均律”是指一个八度有13个音,相邻两个音之间的频率之比相等,且最后一个音频率是最初那个音频率的2倍,设第二个音的频率为f2,第八个音的频率为f8,则 等于(　　)
【思维·引】化归成数列中项、公比的问题求解.【解析】选A.依题意13个音的频率成等比数列,记为{an},设公比为q,则a13=a1q12,且a13=2a1,所以q= 所以
【内化·悟】　在应用性问题中,判断是否为等比数列模型的关键是什么?提示:关键是看增长(缩减)是否按照同一比例.
【类题·通】　关于等比数列在应用问题中的应用首先根据题意判断是否是等比数列模型,其次分析等比数列的首项、公比、项数,最后利用等比数列的通项公式计算解题.
【习练·破】(2020·延庆高二检测)某企业生产A,B两种型号的产品,每年的产量分别为10万支和40万支,为了扩大再生产,决定对两种产品的生产线进行升级改造,预计改造后的A,B两种产品的年产量的增长率分别为50%和20%,那么至少经过________年后,A产品的年产量会超过B产品的年产量(参考数据:lg 2≈0.301 0)(　　) A.6B.7C.8D.9
【解析】选B.设经过n年后,A产品的年产量会超过B产品的年产量,则10×(1+ 50%)n>40×(1+20%)n,化为: >4,取对数可得:n> ≈6.2.所以至少经过7年后,A产品的年产量会超过B产品的年产量.
【加练·固】　　　某单位某年十二月份的产值是同年一月份产值的m倍,那么该单位此年的月平均增长率是________. 【解析】由题意可知,这一年中的每一个月的产值成等比数列,因为 =m,所以月平均增长率为 -1.答案: -1
类型三　等比数列与等差数列的综合应用角度1　灵活设项解题【典例】三个数成等比数列,其积为64,如果第一个数与第三个数各减去1,则这三个数成等差数列,求这三个数.【思维·引】利用等比数列设出前三项,表示出等差数列后求未知数.
【解析】因为三个数成等比数列,设三个数为 ,a,aq,则 ×a×aq=a3=64,所以a=4,所以三个数为 ,4,4q,第一个数与第三个数各减去1为 -1,4,4q-1,则 -1+4q-1=8,即2q2-5q+2=0,解得q=2或 ,所以这三个数为2,4,8或8,4,2.
【素养·探】　在利用等比数列设项解题过程中,常常用到核心素养中的数学运算,通过解方程求公比解题.本例中的条件若改为“其积为512,如果第一个数与第三个数各减去2”,试求这三个数.
【解析】设三个数依次为 ,a,aq,因为 ·a·aq=512,所以a=8.因为 +(aq-2)=2a,所以2q2-5q+2=0,所以q=2或q= ,所以这三个数为4,8,16或16,8,4.
角度2　等差、等比数列性质【典例】已知{an}是等差数列,{bn}是正项等比数列,且b1=1,b3=b2+2,b4=a3+ a5,b5=a4+2a6,则a2 018+b9=(　　)A.2 274B.2 074C.2 226D.2 026【思维·引】分别用等差数列的首项a1、公差d、等比数列的公比q表示出已知条件,求出a1,d,q后求a2 018+b9.
【解析】选A.设等差数列{an}的公差为d,正项等比数列{bn}的公比为q>0,因为b1=1,b3=b2+2,b4=a3+a5,b5=a4+2a6,所以q2=q+2,q3=2a1+6d,q4=3a1+13d,解得q=2,a1=d=1,则a2 018+b9=1+2 017+28=2 274.
【类题·通】等比数列项的设法(1)三数成等比数列常设成 ,a,aq或a,aq,aq2.(2)若四个数成等比数列,可设为 ,a,aq,aq2.若四个正数成等比数列,可设为 , ,aq,aq3.
【习练·破】　设公差不为零的等差数列{an}满足a3=7,且a1-1,a2-1,a4-1成等比数列,则a10等于________. 
【解析】设等差数列{an}的公差为d,则d≠0,则a1=a3-2d=7-2d,a2=a3-d=7-d,a4=a3+d=7+d,由于a1-1,a2-1,a4-1成等比数列,则(a2-1)2=(a1-1)(a4-1),即(6-d)2=(6-2d)(6+d),化简得d2-2d=0,由于d≠0,解得d=2,因此,a10=a3+7d=7+7×2=21.答案:21
　【加练·固】　　　已知数列{an}是由实数构成的等比数列,a1=2,且a2-4,a3,a4成等差数列,则{an}的公比为________. 【解析】因为数列{an}是由实数构成的等比数列,a1=2,且a2-4,a3,a4成等差数列,所以2a3=(a2-4)+a4,即2×2q2=2q-4+2q3,整理,得(q-2)(q2+1)=0,所以{an}的公比q=2.答案:2
1.对任意等比数列{an},下列说法一定正确的是(　　)A.a1,a3,a9成等比数列B.a2,a3,a6成等比数列C.a2,a4,a8成等比数列D.a3,a6,a9成等比数列【解析】选D.设等比数列的公比为q,因为 =q3,即 =a3a9,所以a3,a6,a9成等比数列.
2.已知数列{an}是等比数列,若 =4,则a5=(　　)A.2B.4C.2 D. 【解析】选B.根据题意,数列{an}是等比数列,设其公比为q,若 =4,则 =a3q2=a5=4.
3.(2020·全国Ⅰ卷)设{an}是等比数列,且a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8=(　　)A.12B.24C.30D.32【解题指南】根据已知条件求得q的值,再由a6+a7+a8=a1q5(1+q+q2)可求得结果.
【解析】选D.设等比数列 的公比为q,则a1+a2+a3=a1 =1,a2+a3+a4=a1q+a1q2+a1q3=a1q =q=2,因此,a6+a7+a8=a1q5+a1q6+a1q7=a1q5 =q5=32.
4.(2020·景德镇高二检测)在正项等比数列{an}中,若a3a4a5=3π,则sin(lg3a1+lg3a2+…+lg3a7)的值为________. 
【解析】在正项等比数列{an}中,若a3a4a5=3π= ,所以a4= .所以sin(lg3a1+lg3a2+…+lg3a7)=sin[lg3(a1a2·…·a7)]=sin(lg3 )=sin(lg3 ) 答案:
【新情境·新思维】　已知数列{ }是等比数列,公比为q,则数列{an} (　　)A.是等差数列,公差为lg3qB.是等差数列,公差为3qC.是等比数列,公比为lg3q　D.既不是等差数列,也不是等比数列