【精品练习题】人教版九年级下册数学教材同步练习题 29.3课题学习-制作立体模型同步测试-(新版)新人教版

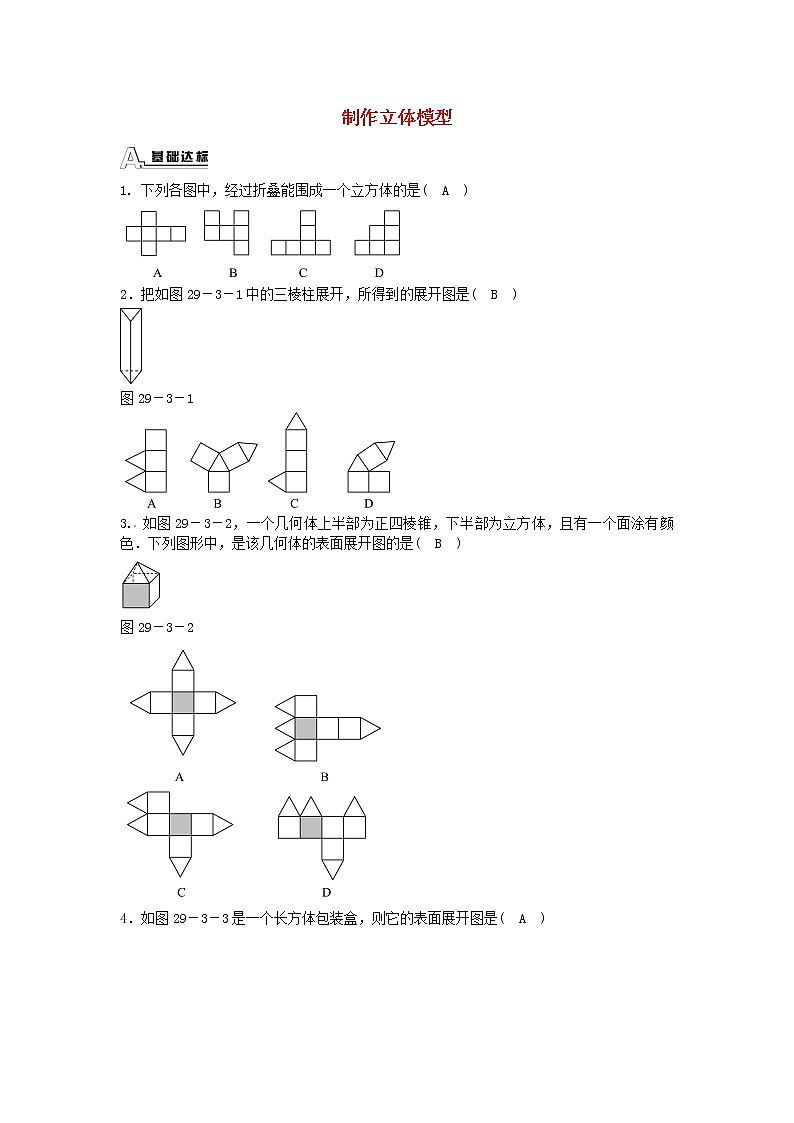
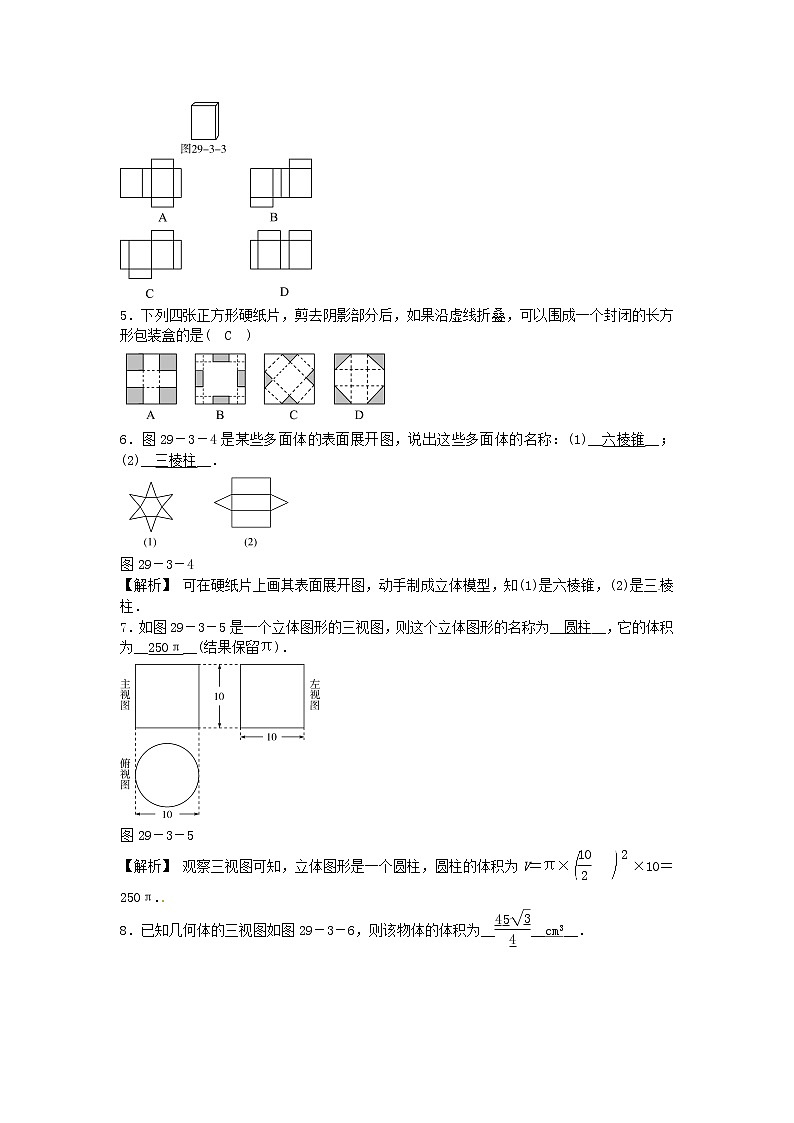
制作立体模型 1. 下列各图中，经过折叠能围成一个立方体的是(　A　)2．把如图29－3－1中的三棱柱展开，所得到的展开图是(　B　)图29－3－13. 如图29－3－2，一个几何体上半部为正四棱锥，下半部为立方体，且有一个面涂有颜色．下列图形中，是该几何体的表面展开图的是(　B　)图29－3－24．如图29－3－3是一个长方体包装盒，则它的表面展开图是(　A　)5．下列四张正方形硬纸片，剪去阴影部分后，如果沿虚线折叠，可以围成一个封闭的长方形包装盒的是(　C　)6．图29－3－4是某些多面体的表面展开图，说出这些多面体的名称：(1)__六棱锥__；(2)__三棱柱__．图29－3－4【解析】 可在硬纸片上画其表面展开图，动手制成立体模型，知(1)是六棱锥，(2)是三棱柱．7．如图29－3－5是一个立体图形的三视图，则这个立体图形的名称为__圆柱__，它的体积为__250π__(结果保留π)．图29－3－5【解析】 观察三视图可知，立体图形是一个圆柱，圆柱的体积为V＝π××10＝250π.8．已知几何体的三视图如图29－3－6，则该物体的体积为____cm3__．图29－3－6【解析】 观察三视图可知物体是一个正三棱柱，如图所示，底面棱长为3 cm，高为5 cm，于是它的体积为V＝×32×5＝(cm3)．9. 将一边长为2的正方形纸片折成四部分，再沿折痕折起来，恰好能不重叠地搭建成一个三棱锥，则三棱锥四个面中最小的面积是(　C　)A．1　　　　　　　B.C.  D.10.如图29－3－7，将一张边长为3的正方形纸片按虚线裁剪后恰好围成一个底面是正三角形的棱柱，这个棱柱的侧面积为(　A　)图29－3－7A．9－3  B．9C．9－  D．9－【解析】∵将一张边长为3的正方形纸片按虚线裁剪后，恰好围成一个底面是正三角形的棱柱，∴这个正三角形的底面边长为1，高为＝，∴侧面为长为3，宽为3－的长方形，面积为9－3.故选A.图29－3－811．小亮利用废纸板做一个三棱柱形无盖的笔筒，设计三棱柱立体模型如图29－3－8所示．(1)请画出立体模型的三视图和表面展开图；(2)做一该笔筒至少要用多少废纸板？【解析】 (1)主视图是长方形，左视图也是长方形，俯视图是一个直角三角形，表面展开图只有下底面无上底面．(2)表面积是3个矩形面积加一个直角三角形的面积．解：(1)三视图如图(1)所示，表面展开图如图(2)所示． 主视图　 左视图　俯视图(1)(2)(2)计算表面积：矩形面积为(6＋8＋10)×14＝24×14＝336(cm2)，直角三角形面积为×8×6＝24(cm2)，表面积为336＋24＝360(cm2)，所以做该笔筒至少要用废纸板360 cm2.12．如图29－3－9是一个纸杯的三视图，你能计算出这个纸杯能装多少水吗？(π取3.14，精确到1 cm3，不计纸的厚度)主视图　　　　　 左视图　　　　　俯视图图29－3－9【解析】 纸杯为一个圆台，圆台上底面直径为6 cm，下底面直径为4 cm，高为8 cm.解：如图所示，设AB为上底面直径，CD为下底面直径，则AB＝6 cm，CD＝4 cm, 延长AC，BD交于O，过O作OM⊥CD于N，并延长交AB于M，则OM⊥AB.∵CD∥AB，∴△OCD∽△OAB，∴＝，即＝，∴ON＝16，∴纸杯能装水的体积是V＝π××(16＋8)－π××16≈159(cm3)．图29－3－1013．如图29－3－10，长方体的底面边长分别为2 cm和4 cm，高为5 cm，若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，求蚂蚁爬行的最短路径长为多少？解：长方体侧面展开图是长方形，长为2×(2＋4)＝12(cm)，宽为5 cm，如图，由勾股定理得蚂蚁爬行的最短路径PQ长为＝13(cm)．