2021版新高考数学一轮复习第四章三角函数解三角形4.7正弦定理余弦定理的应用举例课件新人教B版202011231182

这是一份2021版新高考数学一轮复习第四章三角函数解三角形4.7正弦定理余弦定理的应用举例课件新人教B版202011231182，共52页。PPT课件主要包含了内容索引，易错点索引，解题导思等内容，欢迎下载使用。

必备知识·自主学习核心考点·精准研析核心素养·微专题核心素养测评
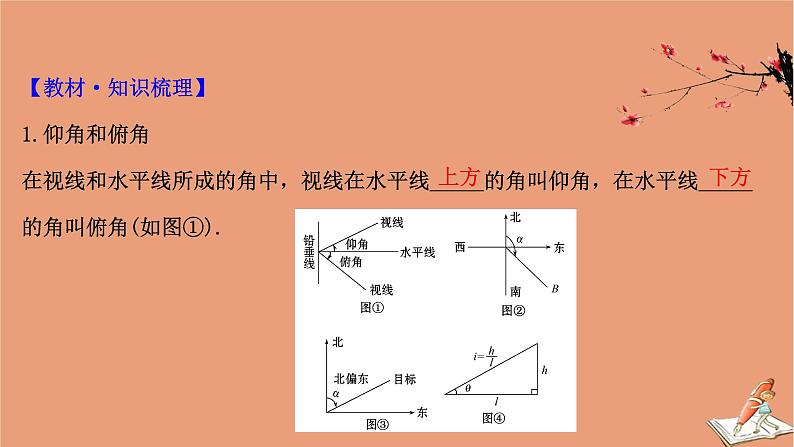
【教材·知识梳理】1.仰角和俯角在视线和水平线所成的角中，视线在水平线_____的角叫仰角，在水平线_____的角叫俯角(如图①).
2.方位角从指北方向顺时针转到目标方向线的水平角，如B点的方位角为α(如图②).3.方向角正北或正南方向线与目标方向线所成的锐角.(1)北偏东α，即由指北方向顺时针旋转α到达目标方向(如图③).(2)北偏西α，即由指北方向逆时针旋转α到达目标方向.(3)南偏西等其他方向角类似.
4.坡角与坡度(1)坡角：坡面与水平面所成的二面角的度数(如图④，角θ为坡角).(2)坡度：坡面的铅直高度与水平长度之比(如图④，i为坡度).坡度又称为坡比.
【常用结论】解与三角形有关的实际应用问题的四个步骤(1)读懂题意，理解问题的实际背景，明确已知和所求，理清量与量之间的关系.(2)根据题意画出示意图，将实际问题抽象成解三角形模型.(3)选择正弦定理或余弦定理求解.(4)将三角形的解还原为实际问题，注意实际问题中的单位、近似计算要求.
【知识点辨析】(正确的打“√”,错误的打“×”)(1)东北方向就是北偏东45°的方向.(　　)(2)俯角是铅垂线与视线所成的角,其范围为 (　　)(3)方位角与方向角其实质是一样的,均是确定观察点与目标点之间的位置关系. (　　)
提示:(1) √.(2)×.俯角是视线与水平线所构成的角.(3)√.
【教材·基础自测】1.(必修5P14问题4改编 )从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为(　　)A.α>β　 B.α=βC.α+β=90°　D.α+β=180°
【解析】选B.由已知及仰角、俯角的概念画出草图,如图,则α=β.
2.(必修5P12问题2改编 )如图所示,设A,B两点在河的两岸,一测量者在A所在的同侧河岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为(　　)
【解析】选A.由正弦定理得 又由题意得∠CBA=30°,所以AB=
3.(必修5P15习题1-2AT1改编 )若点A在点C的北偏东30°,点B在点C的南偏东60°,且AC=BC,则点A在点B的(　　)A.北偏东15°B.北偏西15°C.北偏东10°　D.北偏西10°
【解析】选B.如图所示,∠ACB=90°,又AC=BC,所以∠CBA=45°,而β=30°,所以α=90°-45°-30°=15°.所以点A在点B的北偏西15°.
4.(必修5P15练习AT2改编 ) 如图,飞机的航线和山顶在同一个铅垂面内,若飞机的高度为海拔18 km,速度为1 000 km/h,飞行员先看到山顶的俯角为30°,经过1 min后又看到山顶的俯角为75°,则山顶的海拔高度约为(精确到0.1 km,参考数据: ≈1.732)(　　)A.11.4 km B.6.6 km　 C.6.5 km　 D.5.6 km
【解析】选B.因为AB=1 000× (km),所以BC= ·sin 30°= (km),航线离山顶的高度为h= ×sin 75°= ×sin(45°+ 30°)≈11.4(km).所以山顶的海拔高度约为18-11.4=6.6(km).
5.(必修5P14练习AT1改编 )如图所示,D,C,B三点在地面的同一条直线上,DC=a,从C,D两点测得A点的仰角分别为60°,30°,则A点离地面的高度AB=________. 
【解析】由已知∠DAC=30°,△ADC为等腰三角形,AD= a,所以在Rt△ADB中,AB= AD= a.答案: a
考点一　测量距离问题  【题组练透】1.如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60 m,则河流的宽度BC=(　　)A.240( -1) mB.180( -1) mC.120( -1) mD.30( +1) m
2.一船以每小时15 km的速度向东行驶,船在A处看到一灯塔B在北偏东60°,行驶4小时后,船到达C处,看到这个灯塔在北偏东15°,这时船与灯塔的距离为(　　)A.60 kmB.60 kmC.30 kmD.30 km
3.(2019·衡阳模拟)如图,为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为世纪金榜导学号(　　)A.7 kmB.8 km　C.9 km　D.6 km
4.如图,海中有一小岛C,一小船从A地出发由西向东航行,望见小岛C在北偏东60°,航行8海里到达B处,望见小岛C在北偏东15°,若此小船不改变航行的方向继续前行2( -1)海里,则离小岛C的距离为(　　)世纪金榜导学号A.8( +2)海里　　B.2( -1)海里C.2( +1)海里D.4( +1)海里
【解析】1.选C.记气球在地面的投影为D,在Rt△ABD中,cs 15°= ,又cs 15°=cs (60°-45°)= ,所以AB= .在△ABC中,由正弦定理得 ,所以BC= 2.选A.画出图形如图所示,在△ABC中,∠BAC=30°,AC=4×15 =60 ,∠B=45°,由正弦定理得 所以BC= =60,所以船与灯塔的距离为60 km.
3.选A.在△ABC中,由余弦定理得AC2=AB2+BC2-2AB·BCcs B,即AC2=25+64-2×5×8cs B=89-80cs B.在△ADC中,由余弦定理得AC2=AD2+DC2-2AD·DCcs D,即AC2=25+9-2×5×3cs D=34-30cs D.因为∠B与∠D互补,所以cs B=-cs D,所以 解得AC=7(km).4.选C.BC= 所以离小岛C的距离为
【规律方法】距离问题的常见类型及解法1.类型:测量距离问题常分为三种类型:山两侧、河两岸、河对岸.2.解法:选择合适的辅助测量点,构造三角形,将实际问题转化为求某个三角形的边长问题,从而利用正、余弦定理求解.
【秒杀绝招】　直角三角形解T1,记气球在地面的投影为D,在Rt△ACD中,tan 60°= ,所以CD=60 ,在Rt△ABD中,因为tan 15°= ,tan 15°=tan(60°-45°)= 所以BD=120-60 ,所以BC=CD-BD=120( -1)(m).
考点二　测量高度问题  【典例】1.一架直升飞机在200 m高度处进行测绘,测得一塔顶与塔底的俯角分别是30°和60°,则塔高为(　　)
2.如图,在水平地面上有两座直立的相距60 m的铁塔AA1和BB1.已知从塔AA1的底部看塔BB1顶部的仰角是从塔BB1的底部看塔AA1顶部的仰角的2倍,从两塔底部连线中点C分别看两塔顶部的仰角互为余角.则从塔BB1的底部看塔AA1顶部的仰角的正切值为________;塔BB1的高为________m.世纪金榜导学号 
【解析】1.选A.如图所示. 在Rt△ACD中,CD= =BE,在△ABE中,由正弦定理得 所以AB= ,DE=BC=200- (m).
2.设从塔BB1的底部看塔AA1顶部的仰角为α,则AA1=60tan α m,BB1=60tan 2α m.因为从两塔底部连线中点C分别看两塔顶部的仰角互为余角,所以△A1AC∽△CBB1,所以 所以AA1·BB1=900,所以3 600tan αtan 2α=900,所以tan α= (负值舍去),所以tan 2α= ,BB1=60tan 2α=45(m).答案: 　45
【规律方法】求解高度问题的关注点1.在处理有关高度问题时,要理解仰角、俯角(在铅垂面上所成的角)、方向(位)角(在水平面上所成的角)是关键.2.注意山或塔垂直于地面或海平面,把空间问题转化为平面问题.
【变式训练】(2019·宜春模拟)某工厂实施煤改电工程防治雾霾,欲拆除高为AB的烟囱,测绘人员取与烟囱底部B在同一水平面内的两个观测点C,D,测得∠BCD=75°, ∠BDC=60°,CD=40米,并在点C处的正上方E处观测顶部A的仰角为30°,且CE=1米,则烟囱高AB=________米. 
【解析】∠CBD=180°-∠BCD-∠BDC=45°,在△CBD中,由正弦定理得BC= (米),所以AB=1+tan 30°·CB=1+20 (米).答案:(1+20 )
考点三　测量角度问题
【命题角度1】 方向问题【典例】如图,两座灯塔A和B与海岸观察站C的距离相等,灯塔A在观察站南偏西40°,灯塔B在观察站南偏东60°,则灯塔A在灯塔B的(　　)A.北偏东10°　B.北偏西10°C.南偏东80°D.南偏西80°【解析】选D.由条件及题干图知,∠CAB=∠CBA=40°,又∠BCD=60°,所以∠CBD=30°,所以∠DBA=10°,因此灯塔A在灯塔B的南偏西80°.
【解后反思】解决测量角度问题时有哪些注意事项?提示:1.测量角度时,首先应明确方位角及方向角的含义.2.求角的大小时,先在三角形中求出其正弦或余弦值.3.在解应用题时,要由已知正确画出示意图,通过这一步可将实际问题转化为可用数学方法解决的问题,解题中也要注意体会正、余弦定理使用的优点.
【命题角度2】时间、速度问题【典例】如图,据气象部门预报,在距离某码头南偏东45°方向600 km A处的热带风暴中心正以20 km/h的速度向正北方向移动,距风暴中心450 km以内的地区都将受到影响,则该码头将受到热带风暴影响的时间为(　　)A.14 h　　B.15 h　　C.16 h　　D.17 h
【解析】选B.记现在热带风暴中心的位置为点A,t小时后热带风暴中心到达点B位置,在△OAB中,OA=600 km,AB=20t km,∠OAB=45°,由余弦定理得OB2=6002+400t2-2×20t×600× ,令OB2≤4502,即4t2-120 t+1 575≤0,解得 所以该码头将受到热带风暴影响的时间为
【解后反思】如何求解码头将受到热带风暴影响的时间?提示:已知热带风暴速度,所以将时间问题转化为路程问题,即求出码头受到热带风暴影响时的风暴路线长度.运用解三角形知识求解即可.
【题组通关】 【变式巩固·练】1.如图所示,已知两座花坛A和B与教学楼C的距离相等,花坛A在教学楼C的北偏东40°的方向上,花坛B在教学楼C的南偏东60°的方向上,则花坛A在花坛B的________的方向上. 
【解析】由已知,∠ABC= (180°-80°)=50°,所以花坛A在花坛B的北偏西10°的方向上.答案:北偏西10°
2.在一次抗洪抢险中,某救生艇发动机突然发生故障停止转动,失去动力的救生艇在洪水中漂行,此时,风向是北偏东30°,风速是20 km/h;水的流向是正东,流速是20 km/h,若不考虑其他因素,救生艇在洪水中漂行的速度的方向为北偏东________,大小为________km/h. 
【解析】如图∠AOB=60°,由余弦定理知OC2=202+202-800cs 120°=1 200,故OC=20 ,∠COY=30°+30°=60°.答案:60°　20
【综合创新·练】如图,两座相距60 m的建筑物AB,CD的高度分别为20 m,50 m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角∠CAD等于(　　)　　　　　 　　　　　 　　　　　 A.30°　B.45° C.60° D.75°
【解析】选B.由已知,AD=20 m,AC=30 m,又CD=50 m,所以在△ACD中,由余弦定理得cs∠CAD= 又0°<∠CAD<180°,所以∠CAD=45°,所以从顶端A看建筑物CD的张角为45°.
【核心素养】　数学建模——正、余弦定理解决实际问题 【素养诠释】数学建模是对现实问题进行数学抽象,用数学知识与方法构建数学模型解决问题的素养.在解三角形问题中,主要涉及测量角度、高度等,通过正、余弦定理解决问题,最终解决实际问题.
【典例】国庆阅兵式上举行升旗仪式,在坡度为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆顶端的仰角分别为60°和30°,且第一排和最后一排的距离为10 米.则旗杆的高度为________米. 
【素养立意】 　与实际问题结合,考查用正弦定理、余弦定理解三角形.