2021届二轮（理科数学） 　统计与概率 专题卷（全国通用）

2021届二轮（理科数学） 　统计与概率      专题卷（全国通用）

一、选择题

1、已知变量与正相关，且由观测数据算得样本平均数， ，则由该观测数据算得的线性回归方程可能是（ ）

A.     B.     C.     D.

2、从学号为0～50的高一某班50名学生中随机选取5名同学参加数学测试,采用系

统抽样的方法,则所选5名学生的学号可能是：（   ）

A、5,15,25,35,45   B、1,2,3,4,5

C、2,4,6,8,10      D、 4,13,22,31,40

3、已知回归方程，则该方程在样本处的残差为（   ）

A. 5    B. 2    C. 1    D. -1

4、某超市为了了解“微信支付”与“支付宝支付”的情况（“微信支付”与“支付宝支付”统称为“移动支付”），对消费者在该超市在2019年1-6月的支付方式进行统计，得到如图所示的折线图，则下列判断正确的是（    ）

①这6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多

②这6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大

③这6个月中4月份平均每天使用“移动支付”的次数最多

④2月份平均每天使用“移动支付”比5月份平均每天使用“移动支付”的次数多

A．①③ B．①②③ C．①③④ D．①②③④

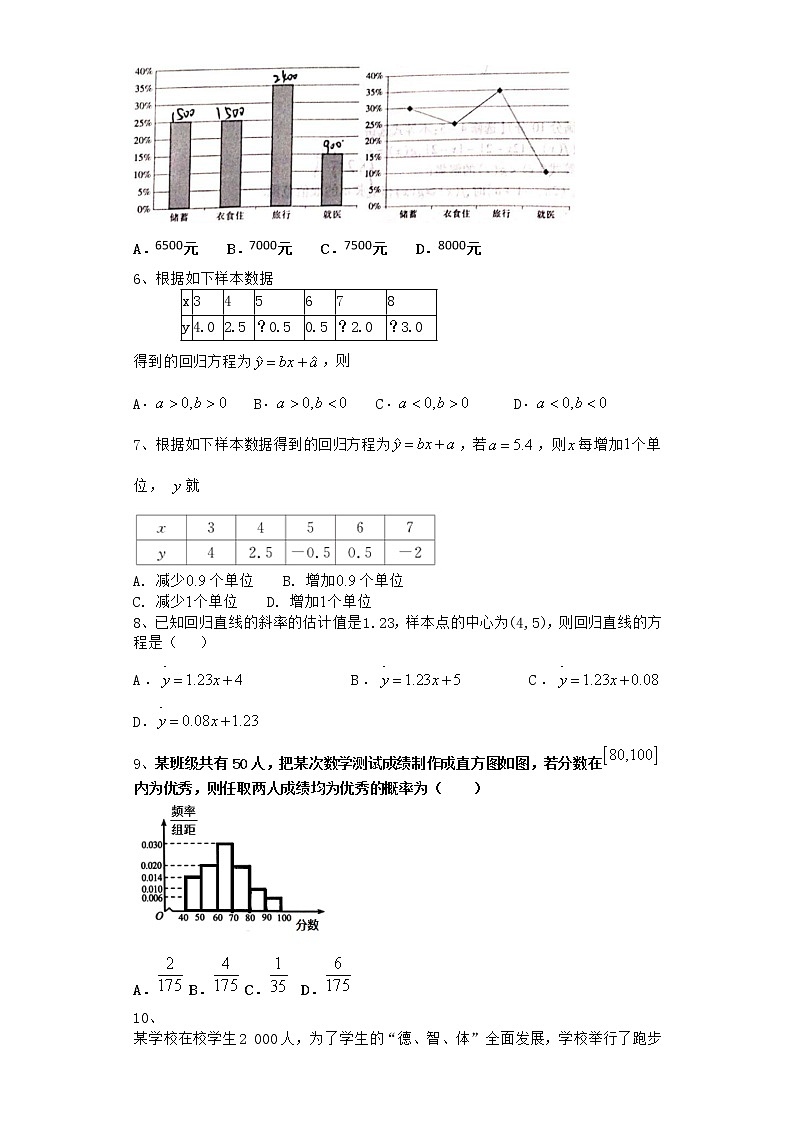
5、若干年前，某教师刚退休的月退休金为元，月退休金各种用途占比统计图如下面的条形图。该教师退休后加强了体育锻炼，目前月退休金的各种用途占比统计图如下面的折线图。已知目前的月就医费比刚退休时少元，则目前该教师的月退休金为（    ）

A．元    B．元    C．元    D．元

6、根据如下样本数据

得到的回归方程为，则

A．     B．    C．  D．

7、根据如下样本数据得到的回归方程为，若，则每增加个单位， 就

A. 减少个单位    B. 增加个单位

C. 减少个单位    D. 增加个单位

8、已知回归直线的斜率的估计值是1.23，样本点的中心为(4,5)，则回归直线的方程是（   ）

A．           B．       C．    D．

9、某班级共有50人，把某次数学测试成绩制作成直方图如图，若分数在内为优秀，则任取两人成绩均为优秀的概率为（    ）

A． B． C． D．

10、

某学校在校学生2 000人，为了学生的“德、智、体”全面发展，学校举行了跑步和登山比赛活动，每人都参加而且只参与其中一项比赛，各年级参与比赛的人数情况如下表：

其中a∶b∶c＝2∶5∶3，全校参与登山的人数占总人数的.为了了解学生对本次活动的满意程度，从中抽取一个200人的样本进行调查，则高三年级参与跑步的学生中应抽取(  )

A．15人        B．30人          C．40人        D．45人

11、下列说法：①对于独立性检验，的值越大，说明两事件相关程度越大，②以模型去拟合一组数据时，为了求出回归方程，设，将其变换后得到线性方程，则的值分别是和，③某中学有高一学生400人，高二学生300人，高三学生200人，学校团委欲用分层抽样的方法抽取18名学生进行问卷调查，则高一学生被抽到的概率最大，④通过回归直线= +及回归系数,可以精确反映变量的取值和变化趋势，其中正确的个数是（    ）

A．     B．     C．     D．

12、一组数据的平均数是4.8，方差是3.6，若将这组数据中的每一个数据都加上60，得到一组新数据，则所得新数据的平均数和方差分别是(　　)

A．55.2,3.6 B．55.2,56.4

C．64.8,63.6 D．64.8,3.6

二、填空题

13、为了调查城市PM2. 5的值，按地域把48个城市分为甲、乙、丙三组，对应的城市数分别为10，18，20.若用分层抽样的方法抽取16个城市，则乙组中应抽取的城市数为_________________．

14、某学校为了调查学生在学科教辅书方面的支出情况，抽出了一个容量为的样本，其频率分布直方图如图所示，其中支出的钱数在的同学比支出的钱数在的同学多26人，则的值为__________．

15、某工厂第一车间有工人1200人，第二车间有工人900人，第三车间有工人1500人，现用分层抽样的方法从这三个车间中抽取一个容量为144的样本进行某项调查，则第二车间应抽取的工人数为______．

16、中外两支女子曲棍球队在去年的国际联赛中，中国队平均每场进球数为3.2，全年比赛进球个数的标准差为3；外国队平均每场进球数为1.8，全年比赛进球个数的标准差为0.3.下列说法正确的是________．

①中国队的技术比外国队好；②外国队发挥比中国队稳定；

③外国队几乎每场都进球；④中国队的表现时好时坏．

三、解答题

17、在某化学反应的中间阶段，压力保持不变，温度从1°变化到5°，反应结果如下表所示（代表温度，代表结果）：

（1）求化学反应的结果对温度的线性回归方程；

（2）判断变量与之间是正相关还是负相关，并预测当温度达到10°时反应结果为多少？

附：线性回归方程中，，.

18、某校200名学生的数学期中考试成绩频率分布直方图如图所示，其中成绩分组区间是，．

（1）求图中的值；

（2）根据频率分布直方图，估计这200名学生的平均分；

（3）若这200名学生的数学成绩中，某些分数段的人数与英语成绩相应分数段的人数之比如下表所示，求英语成绩在的人数．

19、对甲、乙的学习成绩进行抽样分析，各抽5门功课，得到的观测值如下：

问：甲、乙谁的平均成绩最好？谁的各门功课发展较平衡？

参考答案

1、答案A

由回归方程过中心点，将代入方程可知回归方程为

考点回归方程

2、答案A

解：因为系统抽样的特点为等间隔，并且每一组中抽取一个数字，则符合题意的只有选项A，成立。

3、答案D

详解：当x=3时，，4-5=-1，所以方程在样本处的残差为-1.

故答案为：D.

4、答案C

根据折线图，对①②③④逐项分析计算即可.

详解

①由图像知，使用微信支付的总次数比使用支付宝支付的总次数多，故正确；

②图像中纵坐标是消费次数，并不知道消费总额，故错误；

③由图像知，四月份移动支付消费次数更多，所以平均值也最大，故正确；

④二月份平均每天消费次数，五月份平均每天消费次数，，故正确.

故选：C

5、答案D

设目前该教师的退休金为x元，利用条形图和折线图列出方程，求出结果即可．

详解

设目前该教师的退休金为x元，则由题意得：6000×15%﹣x×10%＝100.解得x＝8000.

故选：D．

6、答案B

由表格数据可知随着x的增大y值逐渐减小，因此相关系数，当时

7、答案A

由题中所给的数据可得： ，

回归方程过样本中心点，则： ，

回归直线方程为： ，

则每增加个单位， 就 减少个单位.

本题选择A选项.

8、答案C

9、答案B

先由直方图得到优秀的人数，利用古典概型求概率的公式，分别求解所有的情况，和满足条件的情况，即得解

详解：由直方图知优秀人数为，

所以任取两人成绩均为优秀的概率为，

故选：B

10、答案D

全校参与登山的人数是2 000×＝500，所以参与跑步的人数是1 500，应抽取＝150，c＝150×＝45(人)．

11、答案B

详解：①的观测值，不是刻画两个分类变量之间的关系,故错误。

②则，的值分别是和0.3,故正确

③某中学有高一学生400人，高二学生300人，高三学生200人，高一学生的比重最大，则高一学生被抽到的概率最大，故正确。

④通过回归直线及回归系数，只能大致的（不能精确）反映变量的取值和变化趋势.故错误。

故选B。

12、答案D

首先写出原来数据的平均数的公式和方差的公式，把数据都加上以后，再表示出新数据的平均数和方差的公式，两部分进行比较，即可得到结果.

详解

设这组数据分别为，

由其平均数为，方差是，则有，

方差，

若将这组数据中每一个数据都加上，则数据为，

则其平均数为，

方差为，

故选D.

13、答案6

由题意得乙组中应抽取的城市数为

14、答案

由频率分布直方图可得支出的钱数在的同学有个，支出的钱数在的同学有个，又支出的钱数在的同学比支出的钱数在的同学多26人，所以

故答案为100

15、答案36

首先计算出抽样比，再根据分层抽样的原则计算可得结果.

详解：三个车间共有：人，

抽样比为：

第二车间抽取：人

故答案为：36

16、答案①②③④

17、答案（1）；（2）

∴，，即可求的回归方程；（2）由于变量的值随温度的值增加而增加，故与之间是正相关.将时，代入回归方程即可求出结果.

试题解：（1）由题意：，，，

又，

∴，，

故所求的回归方程为

（2）由于变量的值随温度的值增加而增加，故与之间是正相关.

当时，

18、答案（1）（2）（3）

（2）由平均数的计算方法求解即可；

（3）求出数学成绩在的人数，再根据比例得出英语成绩在的人数，即可得出答案.

详解：（1），

（2）这200名学生的平均分

（3）数学成绩在的人数分别为

设英语成绩在的人数分别为

则英语成绩在的人数为

19、答案解：，；

，；

∵ ，∴ 甲的平均成绩较好，乙的各门功课发展较平衡。