数学八年级上册3 一次函数的图象课文配套课件ppt

这是一份数学八年级上册3 一次函数的图象课文配套课件ppt，共12页。PPT课件主要包含了新课引入，新课讲解，归纳小结，强化训练等内容，欢迎下载使用。

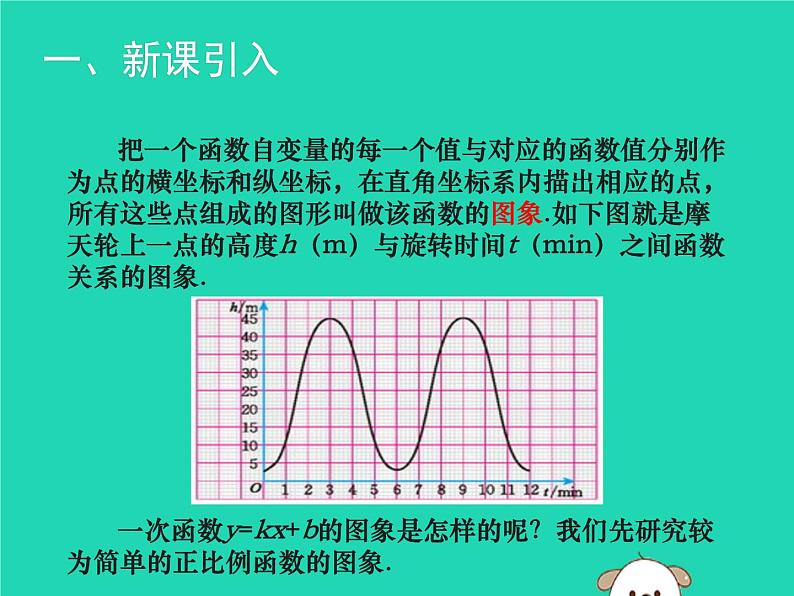
把一个函数自变量的每一个值与对应的函数值分别作为点的横坐标和纵坐标，在直角坐标系内描出相应的点，所有这些点组成的图形叫做该函数的图象.如下图就是摩天轮上一点的高度h（m）与旋转时间t（min）之间函数关系的图象.
一次函数y=kx+b的图象是怎样的呢？我们先研究较为简单的正比例函数的图象.
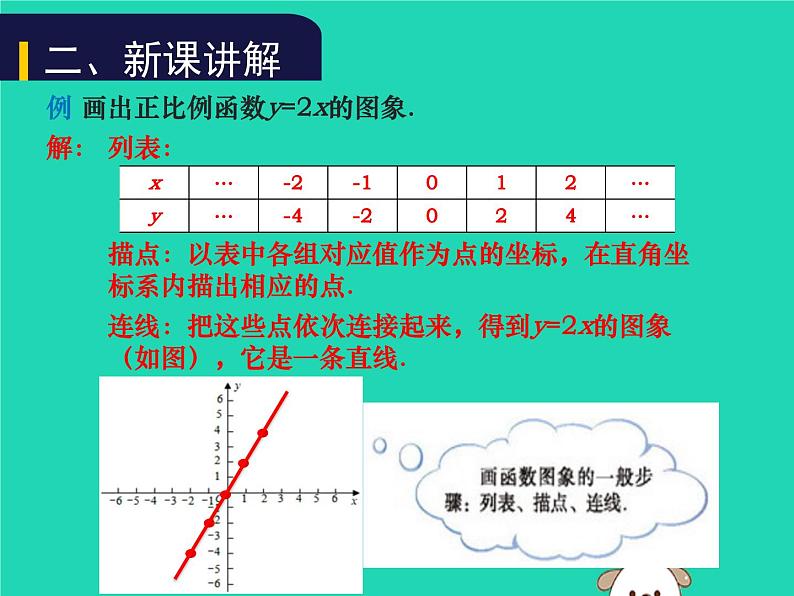
例 画出正比例函数y=2x的图象.
描点：以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点.
连线：把这些点依次连接起来，得到y=2x的图象（如图），它是一条直线.
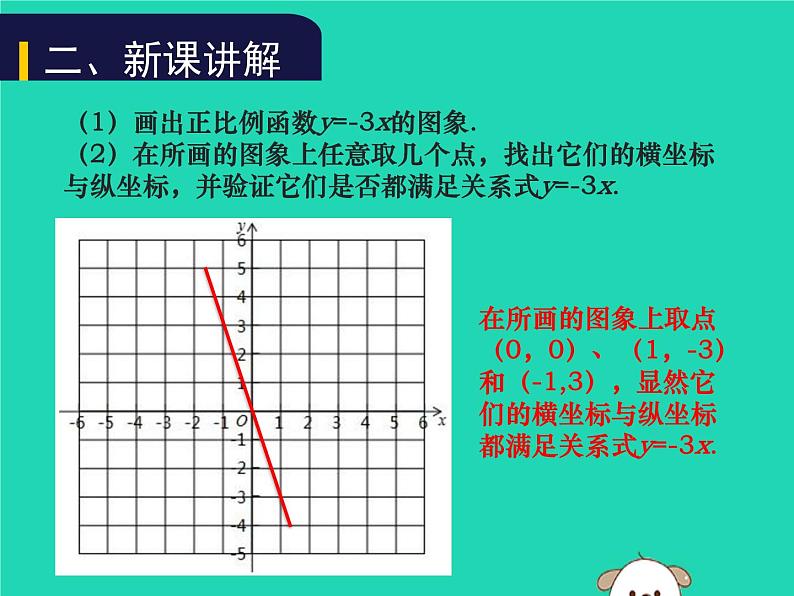
（1）画出正比例函数y=-3x的图象.（2）在所画的图象上任意取几个点，找出它们的横坐标与纵坐标，并验证它们是否都满足关系式y=-3x.
在所画的图象上取点（0，0）、（1，-3）和（-1,3），显然它们的横坐标与纵坐标都满足关系式y=-3x.
（1）满足关系式y=-3x的x，y所对应的点（x，y）都在正比例函数y=-3x的图象上吗？
满足关系式y=-3x的x，y所对应的点（x，y）都在正比例函数y=-3x的图象上.
（2）正比例函数y=-3x的图象上的点（x，y）都满足关系式y=-3x吗？
正比例函数y=-3x的图象上的点（x，y）都满足关系式y=-3x.
（3）正比例函数y=kx的图象有何特点？你是怎样理解的？
正比例函数y=kx的图象是一条经过原点（0，0）的直线.因此，画正比例函数图象时，只要再确定一个点，过这点与原点画直线就可以了.
上述四个函数中，随着x值的增大，y的值分别如何变化？
在正比例函数y=kx中，当k>0时，函数图象从左到右呈上升趋势；当k<0时，函数图象从左到右呈下降趋势.
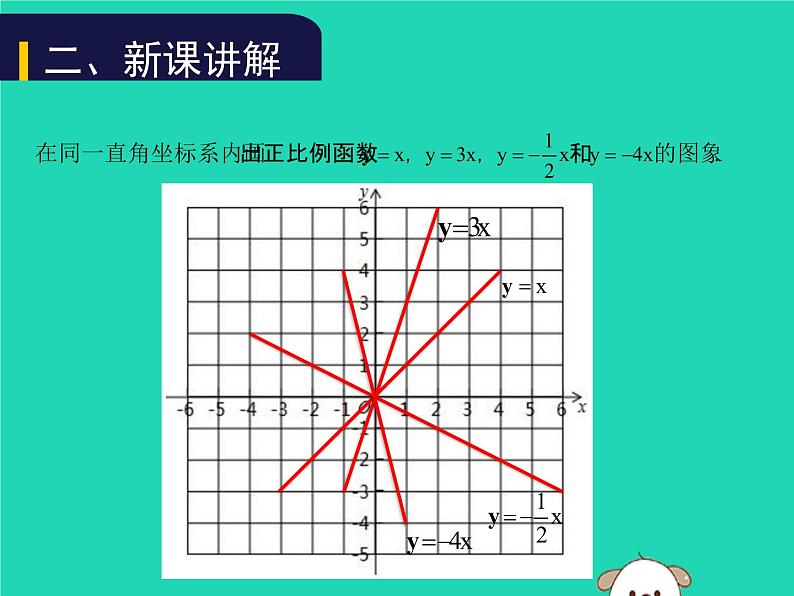
（1）正比例函数y=x和y=3x中，随着x值的增大，y的值都增加了，其中哪一个增加得更快？你能说明其中的道理吗？
y=3x增加得更快. 给定x1，x2（x10,所以3（x2-x1）>（x2-x1）,即对于y=x和y=3x，在自变量的变化情况相同的条件下，y=3x的函数值的增加量大于y=x的函数值的增加量. 故y=3x增加得更快.
（2）类似地，正比例函数y=-½x和y=-4x中，随着x值的增大，y的值都减小了，其中哪一个减小得更快？你是如何判断的？
y=-4x减小得更快. 给定x1，x2（x1-½（x1-x2）,即对于y=-½x和y=-4x，在自变量的变化情况相同的条件下，y=-4x的函数值的减小量大于y=-½x的函数值的减小量. 故y=-4x减小得更快.
1．正比例函数图象的特点.2．对于不同的k，y的值随x的值的变化情况不同.