初中北师大版第二章 实数2 平方根教课课件ppt

这是一份初中北师大版第二章 实数2 平方根教课课件ppt，共23页。PPT课件主要包含了第2课时，平方根，新课导入等内容，欢迎下载使用。

第二章 实数2 平方根(第一课时）
1.了解算术平方根的概念，会用根号表示一个正数的算术平 方根.2.会求一个正数的算术平方根，并解决实际问题.
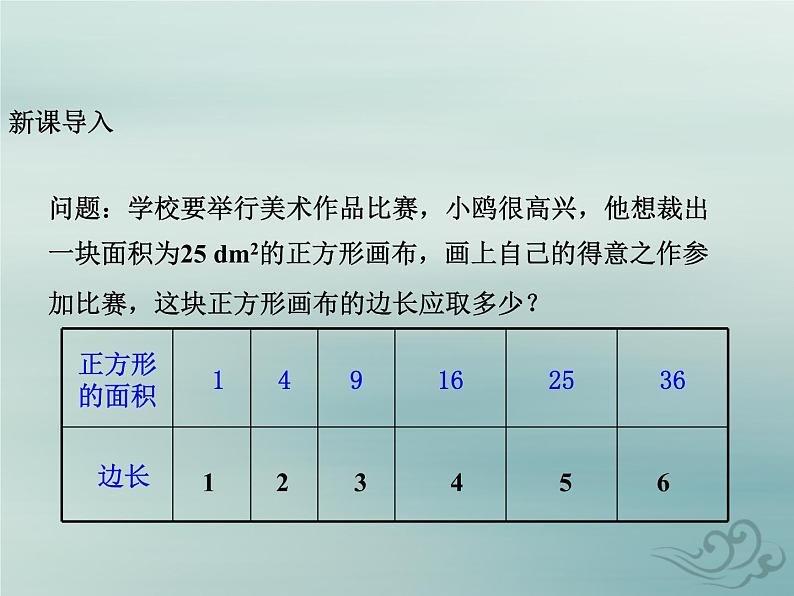
问题：学校要举行美术作品比赛，小鸥很高兴，他想裁出一块面积为25 dm2的正方形画布，画上自己的得意之作参加比赛，这块正方形画布的边长应取多少？
特殊地：0的算术平方根是0.
一般地，如果一个正数x的平方等于a，即x2=a，那么这个正数x就叫做a的算术平方根.记为“ ”，读作“根号a”.
例如：144的算术平方根是12.
【例1】求下列各数的算术平方根：（1）625. （2）0.008 1. （3）6. （4）(-2)². （5） . （6） .
【解析】（1）因为 ，所以625的算术平方根是25，即
（2）因为 ，所以0.008 1的算术平方根是0.09，即
（3）6的算术平方根是
（4）因为 ，所以 的算术平方根是2，即
（5） ，16的算术平方根是4，即 的算术平方根是4.
（6） 所以 的算术平方根是0.5.
【解析】设每块地板砖的边长为x m.由题意，得所以，每块地板砖的边长是0.5 m.
【例2】用大小完全相同的240块正方形地板砖，铺一间面积为60 m2的会议室的地面，每块地板砖的边长是多少？
“欲穷千里目，更上一层楼” 说的是登得高看得远.若观测点的高度为h，观测者视线能达到的最远距离为d≈ ，其中R是地球半径（通常取6 400 km），小丽站在海边一块岩石上，眼睛离地面的高度为20 m，她观测到远处一艘船刚露出海平面，此时该小船离小丽有多远？
【解析】由R=6 400 km、h=0.02 km,得
通过本课时的学习，需要我们掌握：1.算术平方根的定义：一般地，如果一个正数x的平方等于a，即x2=a, 那么这个正数x就叫做a的算术平方根.2.正数的算术平方根是正数，0的算术平方根是0，负数没有算术平方根.
1.了解平方根的概念，会用根号表示一个正数的平方根，并进行相关的计算.2.了解开方和乘方是互逆运算，会利用这个互逆运算求某些非负数的平方根.
设图中的小方格的边长为1，你能分别说出两个长方形的对角线AB，A′B′的长吗？
想一想： 如果一个数的平方等于9，那么这个数是多少？
填一填：写出左圈和右圈中的“？”表示的数：
一般地，如果一个数x的平方等于a，即x2=a，那么这个数x就叫做a的平方根（或二次方根）.
例如，因为3和-3的平方都等于9，我们就说3和-3是9的平方根.也可以说9的平方根是±3.
平方根的表示方法、读法
（1）一个正数有几个平方根？（2）0 有几个平方根？（3）负数呢？
一个正数有两个平方根，它们互为相反数；0只有一个平方根，它是0本身；负数没有平方根.
+1-1+2-2+3-3
x x2
x2 x
求一个数a的平方根的运算，叫做开平方，a叫做被开方数.
可以看出,平方与开平方互为逆运算,根据这种关系可以求出一个数的平方根.
平方与开平方有什么关系？
【例】求下列各数的平方根：（1）25 （2）0.81 （3）15 （4）(-2)² （5）0 （6）-3
【解析】（1）因为 ，所以25的平方根是±5，即
（2）因为 ，所以0.81的平方根是±0.9，即
（3）15的平方根是±
（4）因为 ，所以 的平方根是±2，即
（5）0的平方根是0.
（6）-3没有平方根.