



沪科版七年级下册10.4 平移授课课件ppt
展开平移的定义平移的性质平移作图
如图,传送带上的货物,随着传送带的运动,从一处被移动到另一处;吊车上的物体,随着吊车的运动被上下(或左右)移动,这些都反映了日常生活中,物体沿着某一方向平行移动的现象.
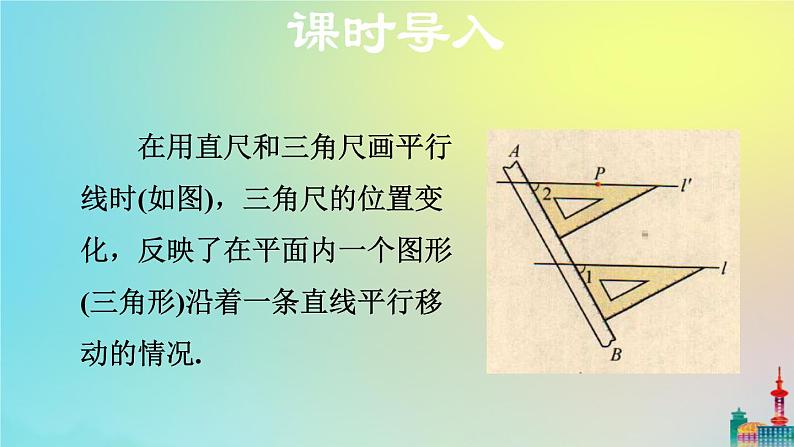
在用直尺和三角尺画平行线时(如图),三角尺的位置变化,反映了在平面内一个图形(三角形)沿着一条直线平行移动的情况.
问题:1. 如图(1),在一张硬纸上剪下一个四边形.
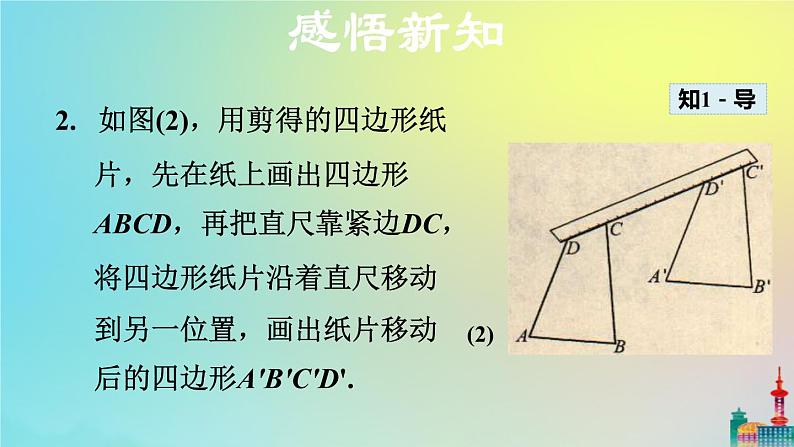
2. 如图(2),用剪得的四边形纸片,先在纸上画出四边形ABCD,再把直尺靠紧边DC,将四边形纸片沿着直尺移动到另一位置,画出纸片移动后的四边形A'B'C'D'.
在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移(translatin).平移时,原图形上的所有点都沿同一个方向移动相同的距离.原图形上一点A平移后成为点A',这样的两点叫做对应点.
1. 定义:在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.要点精析:(1)平移的两个要素:平移的方向(直线方向)和平移距离.(2)平移只改变图形的位置,不改变图形的形状、大小、方向;
(3)平移的方向:可以是上下平移和左右平移;也可以是按任意指定的方向平移;只要是直线方向即可.
2. 如图,三角形ABC经平移后得到三角形A′B′C′,我们把点A和点A′叫做对应点,线段AB和线段A′B′叫做对应边,∠A和∠A′叫做对应角.
3. 易错警示:易丢图形按直线方向移动这一条件.
下列各组图形中,可以经过平移由一个图形得到另一个图形的是( )
A项中两个三角形形状、大小和方向完全相同,符合要求;B项中两个正方形的大小不一样,所以错误;C项中的两个长方形虽然形状和大小相同,但方向不同,所以不是由平移得到的;D项中两个图形形状大小也一样,但方向不同,所以也不是由平移得到的.
判断一个运动是不是平移现象,要紧扣平移定义的特征:一变三不变,即图形的位置改变,而图形的形状、大小、方向都不变.
1 下列现象中,不属于平移的是( )A.滑雪运动员在白茫茫的平坦雪地上向前滑行B.大楼电梯上上下下地迎送客人C.风车在转动D.火车在笔直的铁轨上飞驰而过
2 下列运动属于平移的是( )A.冷水加热过程中,水中小气泡上升成大气泡B.急刹车时汽车在地面上的滑动C.随手抛出的小石子的运动D.随风飘动的风筝在空中的运动
3 以下现象:①打开教室的门时,门的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动,其中属于平移的是( )A.①② B.①③ C.②③ D.②④
4 将图中的图案平移后,可以得到的图案是( )
思考 如图(3),连接 AA'、BB',CC', DD',这些线段的位置、大小分别有怎样的关系?
一个图形和它经过平移后所得的图形中,连接各组对应点的线段互相平行(或在同一条直线上)且相等. 平移只改变图形的位置,不改变图形的形状和大小.
1. 一个图形和它经过平移后得到的图形中,连接各组对应点的线段互相平行(或在同一直线上)且相等.2. 平移只改变图形的位置,不改变图形的形状和大小.
要点精析:(1)连接对应点的线段的长度就是平移距离;(2)从原图上一点到其对应点的方向即起始点到终止点的方向为平移方向.(3)平移前后图形的对应边平行(或在同一直线上)且相等,对应角相等.
如图所示,图形中有两个梯形ABCD和EFGH,其中梯形EFGH是由梯形ABCD向右平移2 cm后得到的,问:(1)线段AE,BF,CG,DH之间有什么数量关系?
(2)AB与EF,BC与FG,CD与GH,AD与EH之间有什么关系?(3)∠A与∠E,∠B与 ∠F,∠C与∠G, ∠D与∠H之间有 什么数量关系?
根据平移的特征可知:平移只改变图形的位置,不改变图形的大小;平移得到的图形与原来的图形是完全一样的,所以对应的线段之间是平行且相等的.
(1)线段AE,BF,CG,DH的长度相等,都为2 cm.(2)AB与EF,BC与FG,CD与GH,AD与EH平行且相等.(3)∠A与∠E,∠B与∠F,∠C与∠G,∠D与∠H对应相等.
(1)平移过程中,对应线段有可能在同一条直线上,对应点的连线也可能在同一条直线上.(2)对应点所连的线段与对应线段是不同的.
1 下列关于图形平移的说法中,错误的是( )A.图形上所有点移动的方向都相同B.图形上所有点移动的距离都相等C.图形上可能存在不动点D.对应点所连的线段相等
2 (中考·宁德)如图,将直线l1沿着AB方向平移得到直线l2,若∠1=50°,则∠2的度数是( )A.40° B.50° C.90° D.130°
图形平移的方向,不限于是水平的,如图. 平移在我们日常生活中是很常见的,利用平移也可以制作很多美丽的图案.你能举出生活中一些利用平移的例子吗?
平移作图的一般步骤: 平移作图是平移基本性质的应用,利用平移可以得到许多美丽的图案,在具体作图时,应抓住作图的“四部曲”——定、找、移、连.(1)定:确定平移的方向和距离;(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;(4)连:按原图顺次连接对应点.
如图,四边形ABCD的顶点A移动到了A′处,作出四边形ABCD平移后的图形.
因为点A移动到了A′处,所以平移的方向就是AA′方向,平移的距离就是线段AA′的长度,要作出平移后的图形,需要先作出点B,C,D的对应点B′,C′,D′,由“对应点所连的线段平行且相等”可知,BB′∥CC′∥DD′∥AA′,BB′=CC′=DD′=AA′,据此可作出点B′,C′,D′,再顺次连接A′,B′,C′,D′即可.
(1)连接AA′;(2)分别过点B,C,D作BB′∥AA′,CC′∥AA′,DD′∥AA′;(3)在BB′上沿射线AA′的方向 截取BB′=AA′,在CC′,DD′上按同样的方法截取CC′=AA′,DD′=AA′;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,即得到四边形ABCD平移后的图形,如图.
画平移图形的方法:首先分析题目的要求,找出平移的方向和距离,再分析已知图形,确定构成图形的关键点,然后根据平移方向和距离平移每个关键点,最后顺次连接所作的每个关键点的对应点,并标出相应的字母,得出平移后的图形.
如图,将周长为8 cm的三角形ABC沿BC方向平移1 cm得到三角形DEF,则四边形ABFD的周长为( )A.6 cm B.8 cmC.10 cm D.12 cm
根据平移的特征,得AD=CF=1 cm,因为平移不改变图形的形状和大小,所以DE=AB,DF=AC,因此四边形ABFD的周长为AB+BC+CF+DF+AD=(AB+BC+DF)+CF+AD=8+1+1=10(cm).
如图,M,N两个单位分别位于一条封闭式街道的两旁,现准备合作修建一座过街天桥,桥建在何处时才能使由M到N的路线最短?并说明理由(注意:桥必须和街道垂直).
将点N向上平移街道的宽度到达点N′处,连接MN′,MN′与AB的交点就是造桥处.
作法如下:(1)作NE⊥AB于点E,交CD于点F;(2)在NE上截取NN′=EF;(3)连接MN′交AB于点P;(4)作PQ⊥CD于点Q,如图,则PQ为要建的天桥.
理由如下:如图,连接QN.因为PQ⊥AB,NE⊥AB,所以PQ∥NE.又因为NN′=EF,EF=PQ,
所以PQ=NN′(相当于将PQ平移到NN′).所以QN=PN′.所以MP+PN′最短(两点之间线段最短),PQ为定值.所以桥建在PQ处由M到N的路线最短.
求两点间的最短路径时,一般先要将两点间的折线改为线段,再用两点之间,线段最短解决.
1 如图所示,从图形B到图形A的变化过程中,下列描述正确的是( )A.向上平移2个单位,向左平移4个单位B.向上平移1个单位,向左平移4个单位
C.向上平移2个单位,向左平移5个单位D.向上平移1个单位,向左平移5个单位
1. 平移不改变图形的大小、方向、形状,只改变图形的位置;图形平移后,对应线段平行(或在同一条直线上)且相等,对应点的连线平行(或在同一条直线上)且相等.2. 图形平移的条件:平移方向和平移距离或一个点平移后的位置.
3. 在平移过程中,对应点所连的线段也可能在一条直线上,当图形平移的方向是沿着一边所在直线的方向时,那么此边上的对应点必在这条直线上。利用平移的特征,作平行线,构造等量关系是解题常用的方法.
沪科版七年级下册10.4 平移集体备课课件ppt: 这是一份沪科版七年级下册<a href="/sx/tb_c27286_t3/?tag_id=26" target="_blank">10.4 平移集体备课课件ppt</a>,共17页。PPT课件主要包含了学习目标,新课导入,观察与思考,概念剖析,可以发现,平移的性质2,典型例题,如图所示,1连接AA,平移作图的步骤等内容,欢迎下载使用。
2020-2021学年10.4 平移教学课件ppt: 这是一份2020-2021学年10.4 平移教学课件ppt,共23页。PPT课件主要包含了归纳总结等内容,欢迎下载使用。
初中沪科版10.4 平移教学ppt课件: 这是一份初中沪科版10.4 平移教学ppt课件,共25页。













