初中数学沪科版八年级下册17.2 一元二次方程的解法一等奖ppt课件

这是一份初中数学沪科版八年级下册17.2 一元二次方程的解法一等奖ppt课件，共20页。PPT课件主要包含了本节课你有什么收获等内容，欢迎下载使用。

能使一元二次方程左右两边相等的
只含有一个未知数（元），
并且未知数的最高次数是 2 的
ax2+bx+c=0
（a≠0， ）
一元二次方程的解（或根）
2、一元二次方程的一般形式是什么？
1、什么是一元二次方程？
3、什么是一元二次方程的解（或根）？
问题 1：什么叫做平方根？用式子如何表示？
如果一个数的平方等于a，那么这个数就叫做 a的平方根.
若x2=a，则x叫做 a的平方根.
如：9的平方根是______
问题 2：平方根有哪些性质？
① 正数有两个平方根，它们互为相反数；② 零的平方根是零；③ 负数没有平方根。
即 x=
问题 3 : 什么叫做开平方运算？
求一个数的平方根的运算叫做 开平方 .
问题 4：根据平方根的意义你能解下列方程吗？
像解x2=4，x2-2=0这样，
求一元二次方程的解的方法
能利用直接开平方法解的一元二次方程应满足的形式为（ ）.
它们互为相反数.
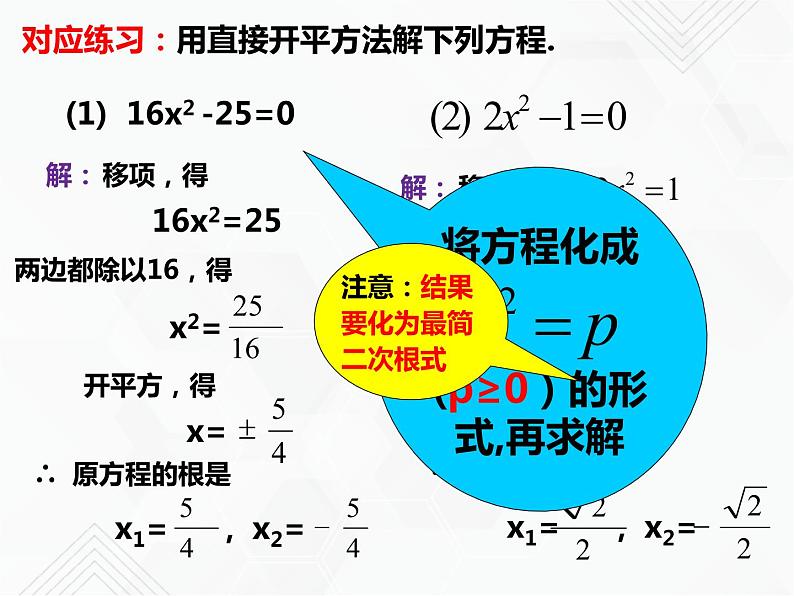
对应练习：用直接开平方法解下列方程.
(1) 16x2 -25=0
将方程化成(p≥0）的形式,再求解
思考：类比上面解方程的过程，你认为应怎样下面的方程.
我们把这种思想称为“降次转化思想.”
直接开平方法的基本思想.
把一个一元二次方程“降次”，
转化为两个一元一次方程。
用直接开平方法还可以解形如 方程
(2) 3(3-2x)2-12 = 0
(1) (x-1)2-4 = 0
3(3-2x)2=12
(3) x2+6x+9=2
(4) (2x-1)2=(x-2)2
2x-1=±(x-2)
或 2x-1=-(x-2)
1、用直接开平方法可解哪些类型的一元二次方程：
把一个一元二次方程“降次”,
转化为两个一元一次方程.
2、直接开平方法的基本思想.
我们把这种思想称为“降次转化思想.”
第一步：把原方程化成 或 这种形式；
3、用直接开平方法解一元二次方程的一般步骤.
第三步：解一元一次方程，求出方程的根.
第二步：开平方，把一元二次方程转化成两个一元一次方程，也就是把二次降为一次；
1、用直接开平方法解下列方程.
(1) (4x- ）(4x+ )=3
(2) (2x-1)2=(3+x)2
2x-1=±(3+x)
或 2x-1=-(3+x)
2、若(a2+b2-3)2=25，求 a2+b2 的值.
∵ (a2+b2-3)2=25
∴ a2+b2-3=±5
即 a2+b2-3=5
或 a2+b2-3=-5
又∵ a2+b2≥0
2、若一元二次方程 ax2=b ( ab>0 ) 的两个根分别是m+1与2m-4，求 的值.
∵ m+1 与 2m-4 分别是一元二次方程 ax2=b ( ab>0 ) 的两个根.
∴ m+1 与 2m-4互为相反数
即 m+1 + 2m-4=0
∴ 方程的两个根分别为
把 x=2 或 x=-2 代入ax2=b中，得
2、用直接开平方法解一元二次方程的一般步骤.
第二步：开平方，把一元二次方程化成一元一次方程，也就是把二次降为一次；
3、直接开平方法的基本思想：
1、什么叫直接开平方法
1、m是方程 x2+x-1=0 的根，求 m3+2m2+2015的值.
∵ m是方程 x2+x-1=0 的一个根
∴ m2+m-1=0
∴ m3+2m2+2015
= m3+m2+m2+2015
= m(m2+1)+m2+2015
= m+m2+2015
2、已知实数a是一元二次方程 x2-2020x+1=0的一个根，求代数式
∵ 实数a是方程 x2-2020x+1=0 的一个根
∴ a2-2020a+1=0
∴ a2+1=2020a，
a2-2020a=-1
= a2-2019a-a
= a2-2020a