





初中数学沪科版八年级下册17.4 一元二次方程的根与系数的关系试讲课课件ppt
展开1、一元二次方程的一般形式是什么?
3、一元二次方程的根的情况怎样确定?
2、一元二次方程的求根公式是什么?
(b2 - 4ac≥0)
有两个不相等的实数根;
一元二次方程的根都可由它的各项系数通过运算得到.
再根据系数a、b、c 的值求出方程的根,
前面我们已经学习用公式法解一元二次方程.
利用一元二次方程的求根公式 ,
与该方程的各项系数之间有怎样的关系呢?
你是否注意到每个方程中的
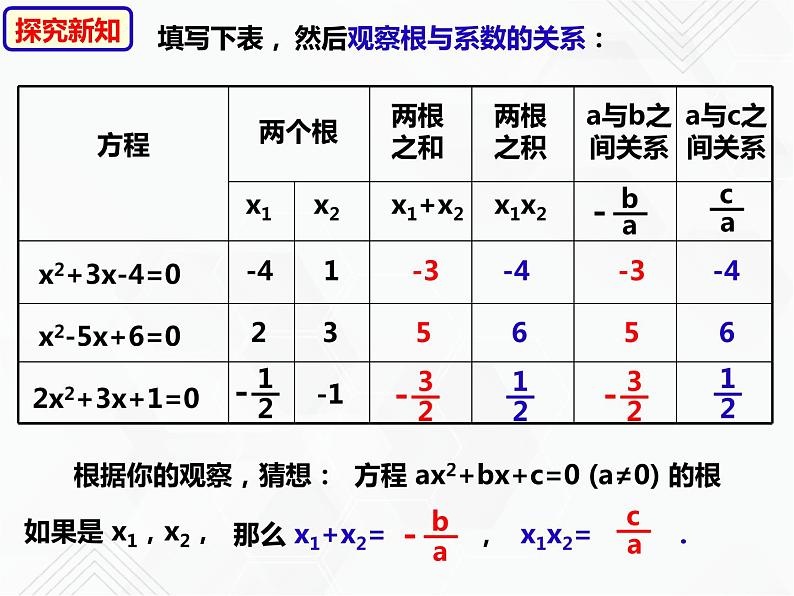
那么 x1+x2= ,
然后观察根与系数的关系:
方程 ax2+bx+c=0 (a≠0) 的根
x1x2= .
你能证明上面的猜想吗?
我们知道,一元二次方程 ax2+bx+c=0 (a≠0) 的两根为
一元二次方程的根与系数之间存在下列关系.
这就是 根与系数 的关系,
如果 ax2+bx+c=0 (a≠0)
x1+x2= ,
1、利用韦达定理的前提条件是
要先把一元二次方程化为一般形式.
这时韦达定理应是:
它的标准形式为x2+px+q=0.
当一元二次方程的二次项系数为1时,
设它的两个根为 x1,x2 ,
x1+x2= ,
1、不解方程,求下列方程的两根的和与积.
(1) x2-5x+2=0
(2) 4x2-2x-7=0
x1+x2=
=5
(4) 2x2+3x=0
(3) 3x2+10=2x2+8x
将原方程化为标准形式,得
x2-8x+10=0
1、利用韦达定理的前提条件为
要把一元二次方程化为一般形式.
只要看这两数之和是否等于 ,
2、判定下列各方程后面括号内的两个数是不是它的两个根.
(1) x2+5x+4=0
(2) x2-6x-7=0
且两数之积是否等于 即可.
(3) 3x2+5x-2=0
( ,2)
(4) x2-8x+11=0
判断所给的两数是不是一元二次方程的根,
∵ 方程 x2-(k+1)x+3k=0 的一个根是 2
综上所述:方程的另一个根是-3 , k的值是-2.
3、已知方程 x2-(k+1)x+3k=0 的一个根是 2 ,求它的另一个根及k的值.
22-2(k+1)+3k=0
∴ 方程的另一个根是-3
设方程的另一个根为 x2.
综上所述::方程的另一个根是 -3 , k的值是 -2.
已知关于x的方程 3x2-19x+m=0 的一个根是1,求它的另一个根及m的值.
综上所述:方程的另一个根是 , k的值是16.
一般先将所求的代数式化成含两根之和,
4、方程 2x2-3x+1=0 的两个根记作 x1,x2,不解方程,
求 x1-x2 的值.
求与方程的根有关的代数式的值时,
求 x12+x22 的值.
=(x1+x2)2 -2x1x2
方程 2x2-3x+1=0 的两个根记作 x1,x2,不解方程,
求 (x1-x2)2 的值.
=x12-2x1x2+x22
=x12+ 2x1x2+x22 - 4x1x2
=(x1+x2)2 - 4x1x2
求 x1-x2 的值.
常用代数式变形方法总汇
2、(x1-x2)2
A、a=b B、b=c C、a=c D、a=b=c
1、关于x的一元二次方程 ax2+bx+c=0 (a≠0) 的两根如果互为倒数,那么( )
A、p>0 且 q>0 B、p>0 且 q<0 C、p<0 且 q>0 D、p<0 且 q<0
2、关于x的方程 x2+px+q 的两根同为负数,则( ).
3、如果方程 x2+kx+8=0 的一根是另一根的2倍,那么K= .
4、 设 a,b 是方程 x2+x-2015=0 的两个实数根,求 a2+2a+b 的值.
∵ a是方程 x2+x-2015=0 的根
∴ a2+a-2015=0
∴ a2+a=2015
又∵ a,b 是方程 x2+x-2015=0 的两个实数根
5、已知 x1,x2 是方程 x2-2x+a=0 的两个实数根,且x1+2x2=5. 求 x1,x2及a的值.
∵ x1,x2 是方程 x2-2x+a=0 的两个实数根
∴ x1+x2=2 ,
又∵ x1x2=a
∴ x1+x2+x2=5
∵ x1+x2=2
综上所述:x1,x2及a的值分别为-1,3,-3.
一元二次方程 x2+2x+2m=0 有两个不相等的实数根.
6、已知关于 x 的一元二次方程 x2+2x+2m=0 有两个不相等的实数根.
(1) 求m的取值范围;
(2) 若 x1,x2 是一元二次方程 x2+2x+2m=0 的两个根,且 x12+x22 =8,求m的值.
∵ 一元二次方程 x2+2x+2m=0 有两个不相等的实数根
∴ 当 时,
∵ x1,x2 是一元二次方程 x2+2x+2m=0 的两个根
∴ x1+x2=-2 ,
又∵ x12+x22 =8
∴ (x1+x2)2- 2x1x2=8
∴ (-2)2 -2×2m=8
7、已知x1,x2 是关于x的方程 x2+2(k-1)x+k2=0 的两个实数根,是否存在常数k,使 成立?若存在,求出k的值;若不存在,请说明理由.
1、一元二次方程的根与系数之间存在什么关系.
这时韦达定理应是:
它的标准形式为x2+px+q=0.
2、当一元二次方程的二次项系数为1时,
初中数学17.4 一元二次方程的根与系数的关系图片课件ppt: 这是一份初中数学17.4 一元二次方程的根与系数的关系图片课件ppt,共13页。PPT课件主要包含了复习引入,合作探究,-2-,探究小结等内容,欢迎下载使用。
初中沪科版17.4 一元二次方程的根与系数的关系课文配套课件ppt: 这是一份初中沪科版17.4 一元二次方程的根与系数的关系课文配套课件ppt,共14页。PPT课件主要包含了自主练习灵活运用,典型例题,1a≠0,2△≥0等内容,欢迎下载使用。
沪科版八年级下册第17章 一元二次方程17.4 一元二次方程的根与系数的关系课堂教学课件ppt: 这是一份沪科版八年级下册第17章 一元二次方程17.4 一元二次方程的根与系数的关系课堂教学课件ppt,共13页。PPT课件主要包含了公式的推导过程,公式的特例,公式的应用,X1+X2,X1X2,和-1,还有其他解法吗,课外作业等内容,欢迎下载使用。













