初中数学17.5 一元二次方程的应用评优课ppt课件

这是一份初中数学17.5 一元二次方程的应用评优课ppt课件，共21页。PPT课件主要包含了本节课你有什么收获等内容，欢迎下载使用。
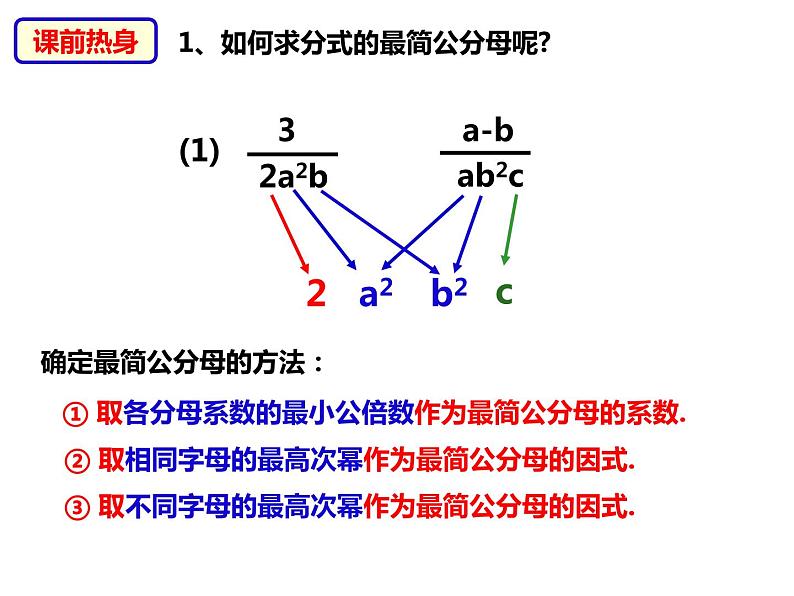
1、如何求分式的最简公分母呢?
确定最简公分母的方法：
① 取各分母系数的最小公倍数作为最简公分母的系数.
② 取相同字母的最高次幂作为最简公分母的因式.
③ 取不同字母的最高次幂作为最简公分母的因式.
方程两边同乘以最简公分母 (x+1)(x-1) ，得
(x+1)2-4=(x+1)(x-1)
最简公分母 (x+1)(x-1)=0.
所以x=1是原分式方程的增根.
使最简公分母不为0的根是原方程的根，
使最简公分母为0的根是原方程的增根，
解分式方程的一般步骤：
(2) 解这个整式方程.
(4) 写出原分式方程的解.
在方程的两边同乘最简公分母，把分式化为整式方程.
把整式方程的根代入最简公分母，
例 1 一组学生组织春游，预计共需费用120元，后来又有2人参加进来，费用不变，这样每人可少分摊 3元，问原来这组学生的人数是多少？
分析：设原来这组学生的人数为x人，
则把题中信息整理成下表:
原来这组学生每人分摊的费用
现在这组学生每人分摊的费用
例 1 一组学生组织春游，预计共需费用120元，后来又有2人参加进来，费用不变，这样每人可少分摊 3元，问原来这组学生的人数是多少？
方程两边同乘以 x(x+2)，整理，得
x2+2x-80=0
答：原来这组学生为8人.
解：设原来这组学生的人数为x人.
x1=-10 ，x2=8
解分式方程应用题时，所得根不仅要检验根是否为增根，还要考虑它是否符合题意.
则中巴车每小时行驶(x+20)千米.
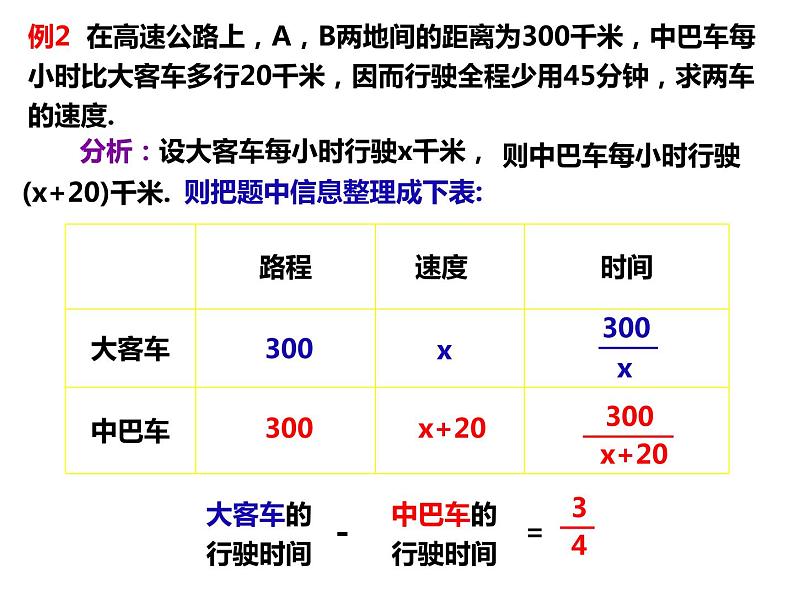
例2 在高速公路上，A，B两地间的距离为300千米，中巴车每小时比大客车多行20千米，因而行驶全程少用45分钟，求两车的速度.
分析：设大客车每小时行驶x千米，
则中巴车每小时行驶(x+20)千米.
解：设大客车每小时行驶x千米，
方程两边同乘以 4x(x+20)，整理，得
x2+20x-8000=0
x1=80 ，x2=-100
题中某个含原未知数 x的式子，
因此，我们可以通过换元法来解.
可以发现两个分式互为倒数.
先用一个新的未知数 y
设 y= ，
方程两边同乘以 2y，整理，得
y1= ，
化简 ，得
化简 ，得
(-1)2-4×2×2
∴ 这个方程没有实数根
经检验：x1=x2=-1 是原方程的根
∴ 这个方程的根为 x1=x2=-1
2、 (泸州市中考) 某品牌瓶装饮料每箱价格26元，某商店对该瓶装饮料进行“买一送三”促销活动，即整箱购买，则买一箱送三瓶，这相当于每瓶比原价便宜了0.6元，问该品牌饮料一箱有多少瓶？
分析：设该品牌饮料一箱有 x 瓶，
2、 (泸州市中考) 某品牌瓶装饮料每箱价格26元，某商店对该瓶装饮料进行“买一送三”促销活动，即整箱购买，则买一箱送三瓶，这相当于每瓶比原价便宜了0.6元，问该品牌饮料一箱有多少瓶？
解：设该品牌饮料一箱有x瓶.
方程两边同乘以 x(x+3)，整理，得
x2+3x-130=0
答：该品牌饮料一箱有10瓶.
x1=10 ，x2=-13
则把题中信息整理成下表:
3、 某车间加工300个零件，加工完80个以后，改进了操作方法，每天能多加工15个，一共用了6天完成任务.求改进操作方法后每天加工的零件个数.
分析：设改进操作方法后每天加工零件x个，
则改进操作方法前每天加工零件（x-15）个.
解：设改进操作方法后每天加工零件x个,
方程两边同乘以 x(x-15)，整理，得
x2-65x+550=0
答：改进操作方法后每天加工零件55个.
x1=55 ，x2=10
则提高后的工作效率为 (1+20%)x .
4、 某市为了进一步缓解交通拥堵现象，决定修建一条从市中心到飞机场的轻轨铁路，为了使工程能提前三个月完成，需要将原来的工作效率提高20%，问原计划完成这项工程需要几个月？
分析：设原来的工作效率为 x，
则提高后的工作效率为 (1+20%)x .
解：设原来的工作效率为 x，
方程两边同乘以 (1+20%)x，整理，得
∴ 原计划完成这项工程的时间为：