沪科版17.1 一元二次方程优质课课件ppt

这是一份沪科版17.1 一元二次方程优质课课件ppt，共59页。PPT课件主要包含了一元二次方程的应用等内容，欢迎下载使用。
能使一元二次方程左右两边相等的
只含有一个未知数（元），
并且未知数的最高次数是 2 的
ax2+bx+c=0
（a≠0， ）
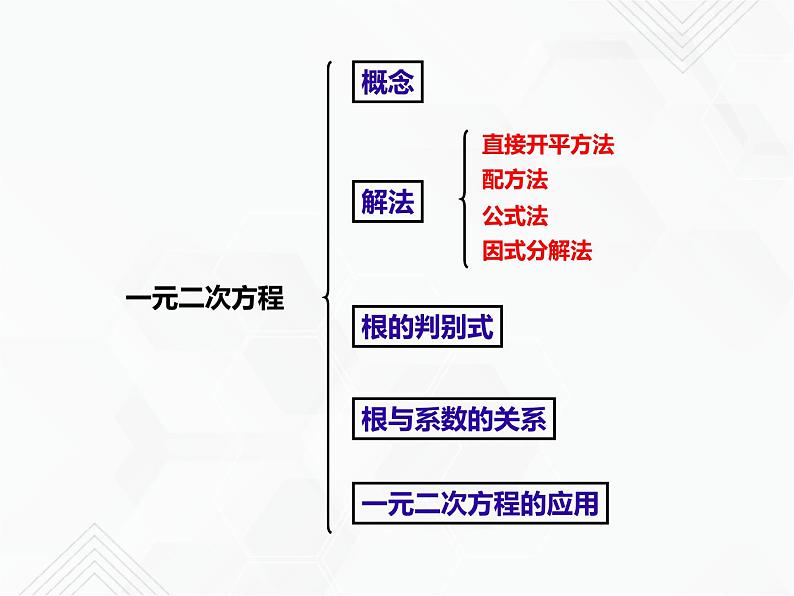
一元二次方程的解（或根）
2、一元二次方程的一般形式是什么？
1、什么是一元二次方程？
3、什么是一元二次方程的解（或根）？
1、判断下列方程中，哪些是关于x的一元二次方程？
(2) 4x2+3x-2=(2x-1)2
(3) x3-x+4=0
(4) x2-2y-3=0
(5) (m+1)x2+3x+1=0
一元二次方程必须满足三个条件
① 只含有一个未知数（元）
2、若方程 是关于x的一元二次方程，求m的值.
∵ 是关于x的一元二次方程
∴
所以既要保证未知数的最高次数是2，
又要保证二次项系数不等于 0 .
注意： 因为所给方程是关于x的一元二次方程，
3、 已知关于x的方程 (k2-1)x2+(k+1)x-2=0.
(1) 当k为何值时是一元一次方程？
∴ 当k=1时，原方程是一元一次方程
(2) 当k为何值时是一元二次方程？
∴ 当k≠±1时，原方程是一元二次方程
4、已知关于x的一元二次方程 (m-2)x2+3x+m2-4=0 有一个根是 0，求m的值.
∵ 0是方程 (m-2)x2+3x+m2-4=0 的一个根
又∵ 方程 (m-2)x2+3x+m2-4=0 是关于x的一元二次方程
因此，求一元二次方程中的字母的值时，
只需把已知方程的根代入原方程就可以求出字母的值.
注意： 方程的根就是使方程左右两边相等的未知数的值，
5、（2018扬州中考）若 m 是方程 2x2-3x-1=0 的一个根，求 6m2-9m+2015 的值.
∵ m是方程 2x2-3x-1=0 的一个根
∴ 2m2-3m-1=0
∴ 2m2-3m=1
∴ 6m2-9m+2015
= 3（2m2-3m）+2015
6、已知实数a是一元二次方程 x2-2020x+1=0的一个根，求代数式
∵ 实数a是方程 x2-2020x+1=0 的一个根
∴ a2-2020a+1=0
∴ a2+1=2020a，
a2-2020a=-1
= a2-2019a-a
= a2-2020a
7、m是方程 x2+x-1=0 的根，求 m3+2m2+2015的值.
∵ m是方程 x2+x-1=0 的一个根
∴ m2+m-1=0
∴ m3+2m2+2015
= m3+m2+m2+2015
= m(m2+1)+m2+2015
= m+m2+2015
1、解一元二次方程的方法有哪些？
2、解一元二次方程的基本思想是什么？
转化为两个一元一次方程，
把一个一元二次方程“降次”，
我们把这种思想称为“降次转化思想.”
用直接开平方法解下列方程.
① 把原方程化成 或 这种形式；
用直接开平方法解一元二次方程的一般步骤.
③ 解一元一次方程，求出方程的根.
② 开平方，把一元二次方程化成一元一次方程，也就是把二次降为一次；
形如 或 的一元二次方程.
(1) 2x2-3x-1=0
当二次项系数1，且一次项系数是偶数时，用 较简单
(2) x2+2x-9999=0
x2+2x+1=9999+1
(x+1)2=10000
用 配方法 解一元二次方程的步骤:
① 把方程化为一般形式，
⑤ 写出一元二次方程的两个根.
把常数项移到方程的右边；
方程两边同时加上一次项系数绝对值
当方程右边是非负数时，
用直接开平方法解方程.
∴ b2 - 4ac=
将原方程化成标准形式，得
22 - 4×2×(-1)=
(a≠0，且b2-4ac≥0)
（b2 - 4ac ≥0）
代入求根公式求解；
用公式法解一元二次方程的一般步骤：
① 把一元二次方程化为一般形式 ax2+bx+c=0 (a≠0)
② 确定方程中 a，b，c 的值
③ 求出 b2 - 4ac 的值
④ 若 b2 - 4ac≥0 ，
若 b2 - 4ac