初中数学沪科版八年级下册18.1 勾股定理一等奖ppt课件

这是一份初中数学沪科版八年级下册18.1 勾股定理一等奖ppt课件，共19页。PPT课件主要包含了勾股定理公式变形，感悟与收获等内容，欢迎下载使用。

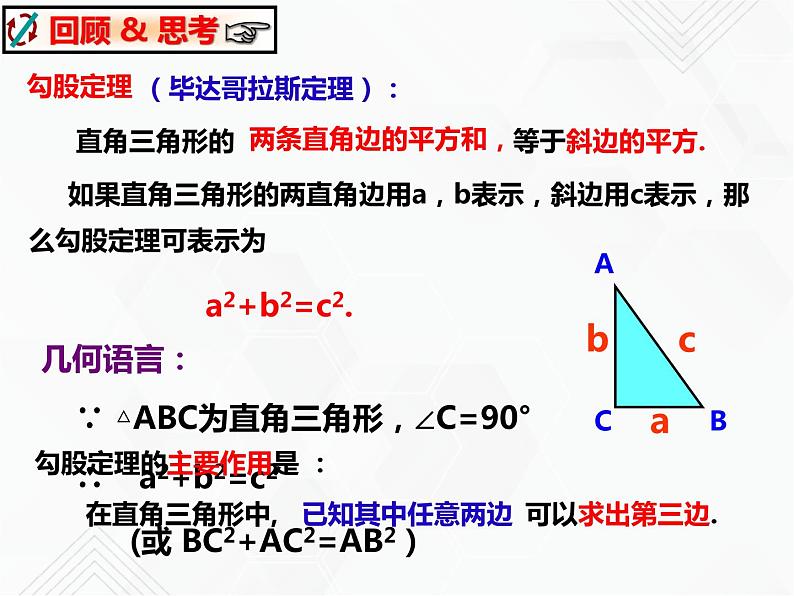
如果直角三角形的两直角边用a，b表示，斜边用c表示，那么勾股定理可表示为
∴ a2+b2=c2
∵ △ABC为直角三角形，∠C=90°
(或 BC2+AC2=AB2）
勾股定理的主要作用是 ：
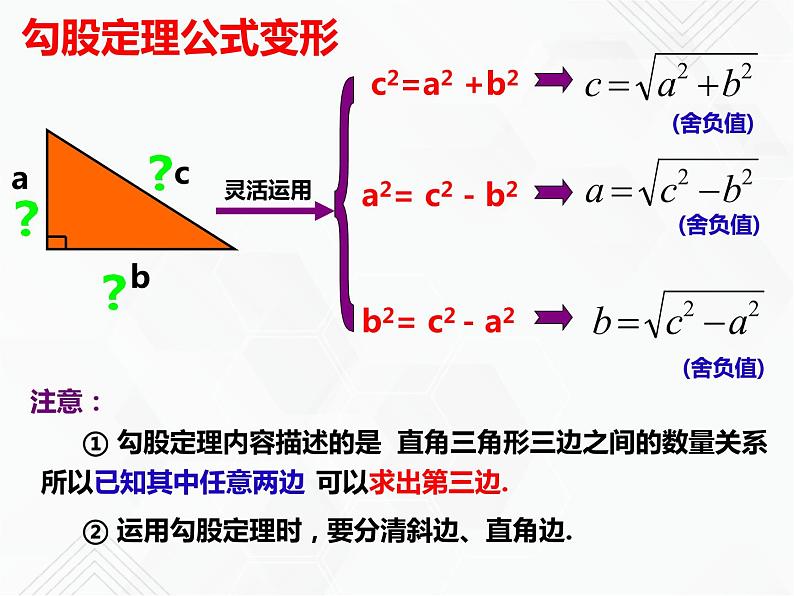
b2= c2 - a2
a2= c2 - b2
① 勾股定理内容描述的是
直角三角形三边之间的数量关系

古代笑话一则 有一人拿着一根杆子进屋门，横着拿，不能进，竖着拿，也不能进，干脆将其折断，才解决了问题。请问同学们这样是真正解决了问题了吗？让你做的话，你感觉怎么办合适？
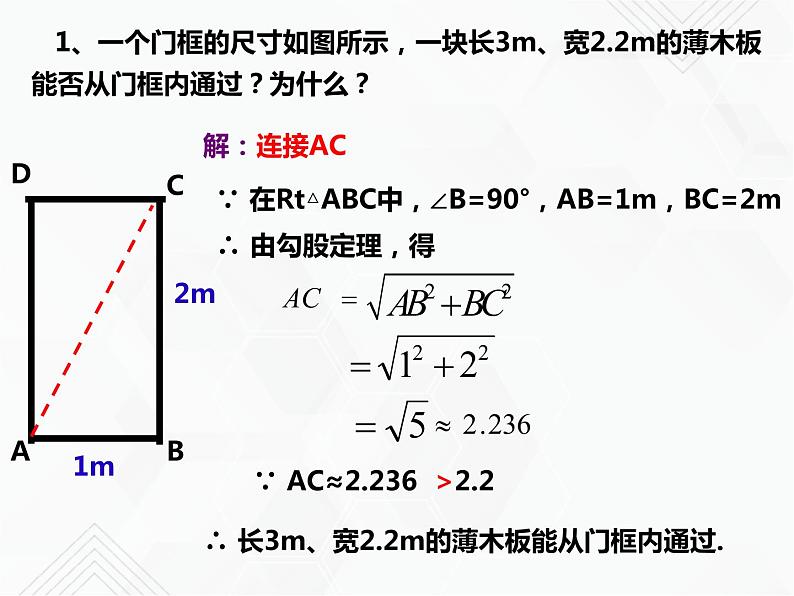
∵ 在Rt△ABC中，∠B=90°，AB=1m，BC=2m
1、一个门框的尺寸如图所示，一块长3m、宽2.2m的薄木板能否从门框内通过？为什么？
∴ 长3m、宽2.2m的薄木板能从门框内通过.
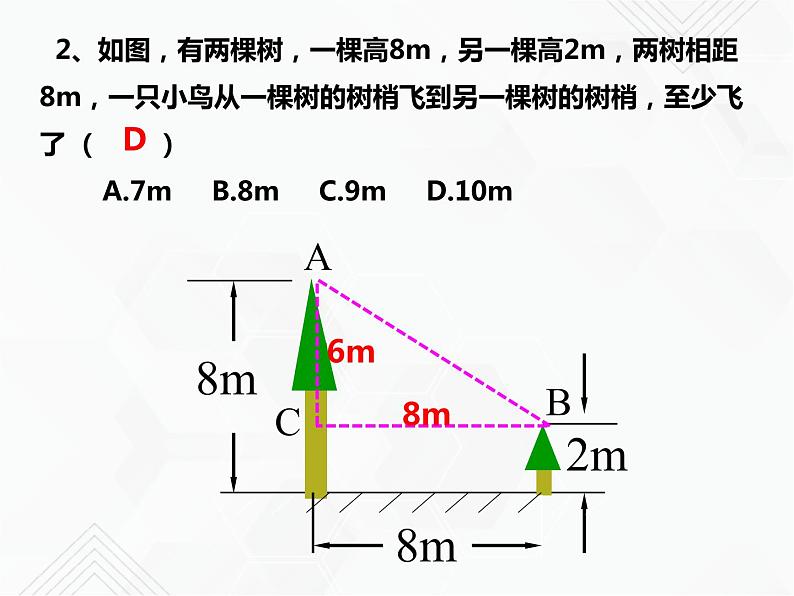
2、如图，有两棵树，一棵高8m，另一棵高2m，两树相距8m，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了 （ ） A.7m B.8m C.9m D.10m
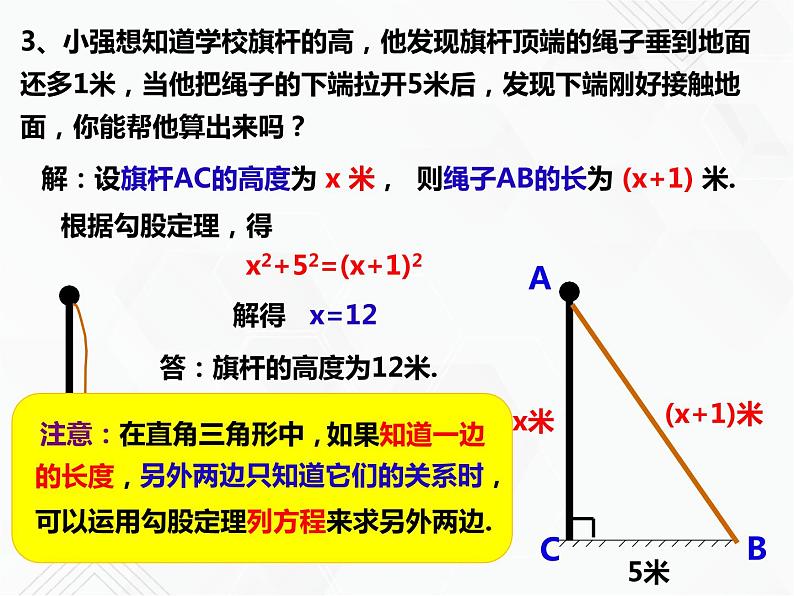
3、小强想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，你能帮他算出来吗？
解：设旗杆AC的高度为 x 米，
则绳子AB的长为 (x+1) 米.
x2+52=(x+1)2
答：旗杆的高度为12米.
如果知道一边的长度，
另外两边只知道它们的关系时，
注意：在直角三角形中，
可以运用勾股定理列方程来求另外两边.
另外两边只知道它们的关系时，
应用勾股定理解决实际问题的一般思路：
方程思想是解决数学问题常用的重要思想
1、在解决实际问题时，
再运用勾股定理解决实际问题。
首先要画出适当的示意图，
将实际问题抽象为数学问题，
并构建直角三角形模型，
2、在直角三角形中，
如果知道一边的长度，
可以运用勾股定理列方程来求另外两边.
4、在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形，在水池的中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，请问这个水池的深度和这根芦苇的长度各是多少？
解：设水池的水深AC为x尺，
则这根芦苇长AD 和AB 为 (x+1) 尺.
52 + x2 = (x+1)2
答：水池的水深12尺，这根芦苇长13尺。
5. 如图，一架梯子长25m，斜靠在一面墙上，梯子底端离墙 7m.
(1) 这个梯子的顶端距地面有多高？
梯子的顶端距地面的高度：
(2) 如果梯子的顶端下滑了4m，那么梯子的底端在水平方向上滑动了几米？
则梯子的底端水平滑动距离也为 xm.
(3) 当梯子的顶端下滑的距离与梯子的底端水平滑动距离相等时，这时梯子的顶端距离地面有多高？
设梯子的顶端下滑的距离为 x m，
∴ 梯子的顶端下滑的距离为17米
∴ 梯子顶端距离地面的高度为
AB是伸长后的云梯，
6、现有一楼房发生火灾，消防队员决定用消防车上的云梯救人，如图，已知云梯最多只能伸长到10m，消防车高3m，求人时云梯伸至最长，在完成从9m高处救人后，还要从12m高处救人，这时消防车要从原处再向着火的楼房靠近多少米？(精确到0.1m)
与楼房ED的交点为O，
则OB＝9-3=6(m)，
OD＝12-3=9(m).
设AC=x，则 OC=8-x，
OC2+OD2＝CD2
即 (8－x)2+92＝102
7、如图所示，已知△ABC中，∠ACB=90°，AB=5cm，BC=3cm，CD⊥AB于D，求CD的长.
解：∵ 在 Rt△ABC 中，∠ACB=90°， AB=5cm，BC=3cm
又∵ Rt△ABC的面积
另两边可通过重合图形找到数量关系，
这个直角三角形一般已知一边，
其解题步骤为：
要紧扣折叠前后的对应边，对应角相等，
1、如图，小颍同学折叠一个直角三角形的纸片，使A与B重合，折痕为DE，若已知AC=10cm，BC=6cm，你能求出CE的长吗？
① 利用重合的图形传递数据
便能利用勾股定理列方程求解.
2、 如图，有一块直角三角形纸片，两直角边AB=6cm，BC=8cm，现将三角形纸片沿直线AD折叠，使点B落在AC上，与点E重合，求DE的长度.
3、矩形ABCD如图折叠，使点D落在BC边上的点F处，已知AB=8，BC=10，求折痕EF的长.