数学八年级下册第19章 四边形19.1 多边形内角和优秀ppt课件

这是一份数学八年级下册第19章 四边形19.1 多边形内角和优秀ppt课件，共33页。PPT课件主要包含了本节课你有什么收获等内容，欢迎下载使用。

(n为不小于3的整数)
3、n边形的内角和等于
(n-2)•180°
这些对角线把n边形分成 个三角形.
5、n边形一共可以作 条对角线.
4、从n边形一个顶点出发，
可作 条对角线，
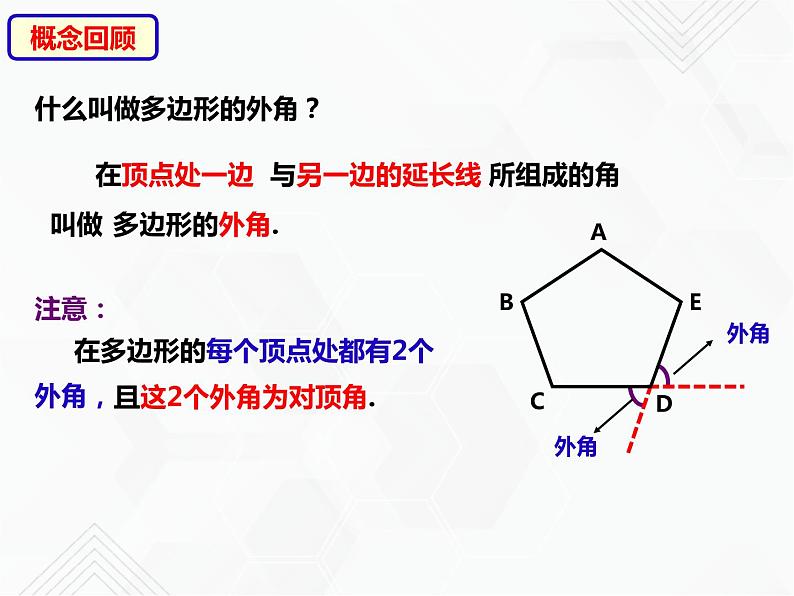
不在同一条直线上的线段
所组成的角
在多边形的每个顶点处都有2个外角，
且这2个外角为对顶角.
什么叫做多边形的外角？
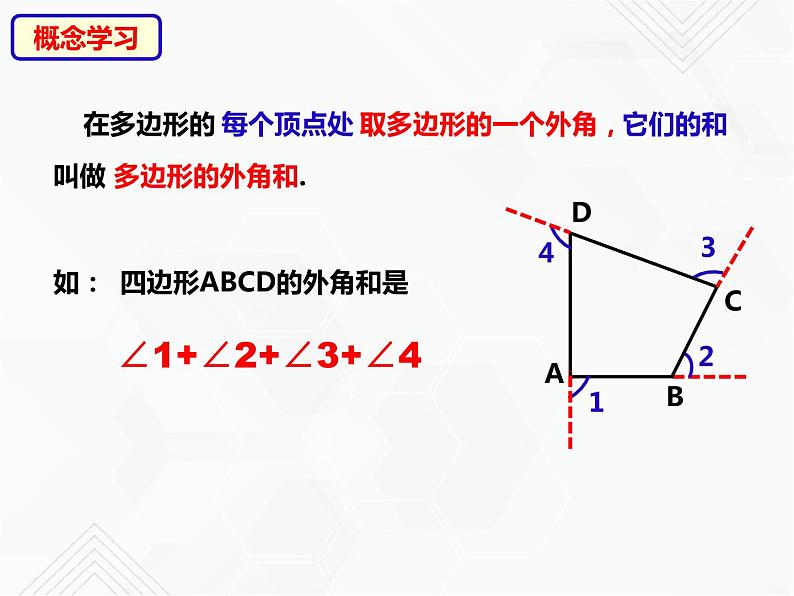
叫做 多边形的外角和.
∠1+∠2+∠3+∠4
四边形ABCD的外角和是
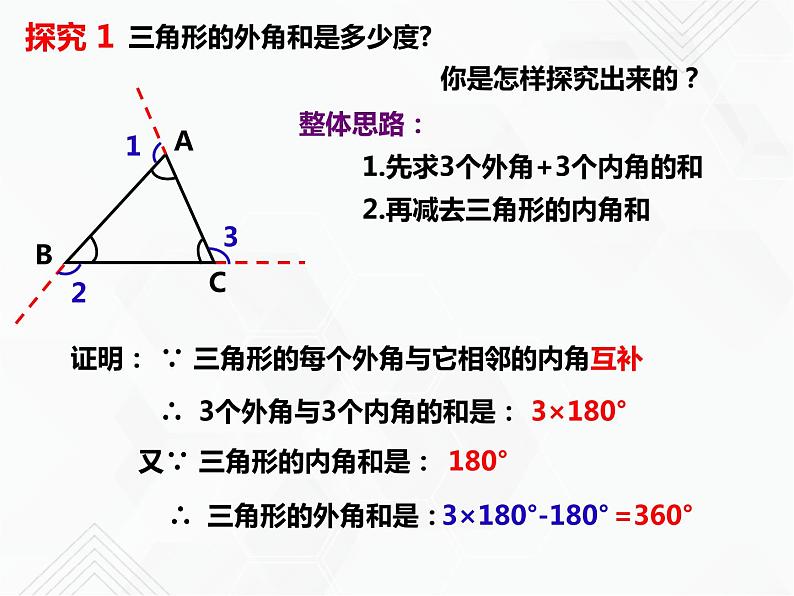
三角形的外角和是多少度?
整体思路： 1.先求3个外角+3个内角的和 2.再减去三角形的内角和
∴ 三角形的外角和是：
又∵ 三角形的内角和是：
∴ 3个外角与3个内角的和是：
∵ 三角形的每个外角与它相邻的内角互补
3×180°-180°
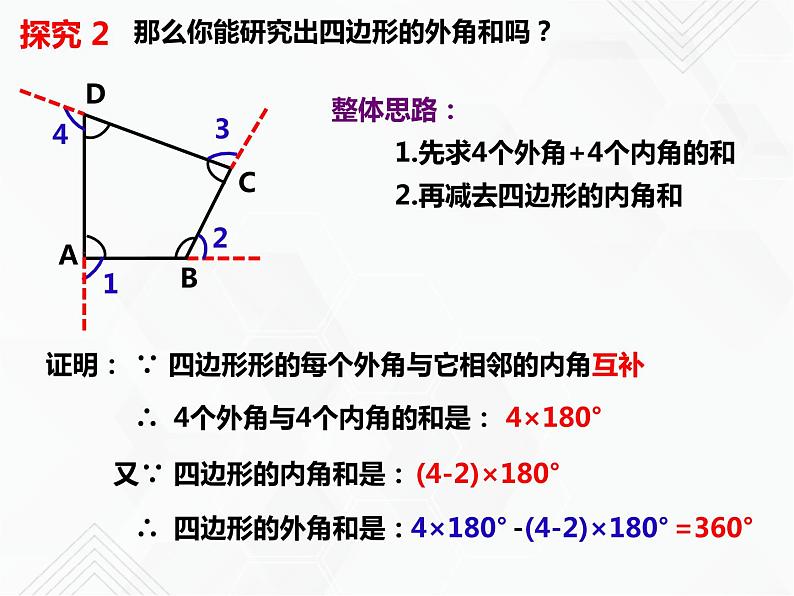
那么你能研究出四边形的外角和吗？
整体思路： 1.先求4个外角+4个内角的和 2.再减去四边形的内角和
∴ 四边形的外角和是：
又∵ 四边形的内角和是：
∴ 4个外角与4个内角的和是：
∵ 四边形形的每个外角与它相邻的内角互补
-(4-2)×180°
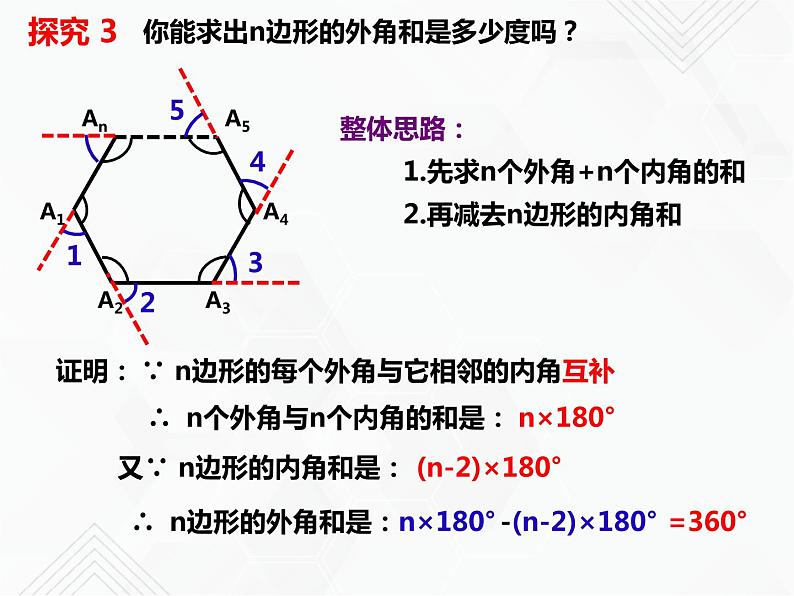
整体思路： 1.先求n个外角+n个内角的和 2.再减去n边形的内角和
你能求出n边形的外角和是多少度吗？
∴ n边形的外角和是：
又∵ n边形的内角和是：
∴ n个外角与n个内角的和是：
∵ n边形的每个外角与它相邻的内角互补
-(n-2)×180°
一个外角相加而得到的，
而不是所有外角相加的和.
∴ 这个多边形是八边形.
一个多边形的内角和等于它的外角和的3倍，它是几边形？
设这个多边形的边数为n.
认真观察下面一组图形，它们有什么共同特点？
它们的各个内角角都相等
这样的多边形叫做 .
(1) 各条边都相等的多边形是正多边形.
对应练习 下列图形是不是正多边形？
由上面的结论判定下列说法正确吗？
(2) 各个角都相等的多边形是正多边形.
(n-2) ·180°
① 正n边形的每一个内角
② 正n边形的每一个外角
1、[北京中考] 若正多边形的一个内角是150°，则该正多边形的边数是（ ）.
A.6 B.12 C.16 D.18
设多边形的边数为n.
（n-2) ·180°= 150°· n

2、求正十二边形的每个内角和每个外角的度数？
正十二边形的每个内角的度数为
(12-2)×180°
3、一个多边形，每一个外角都等于45°，这个多边形是几边形，它的内角和是多少？
∵ 多边形的外角和是360°，
∴ 这个多边形的内角和为
且每一个外角都等于45°
当小华第一次回到出发地点A时，
4、[湖北十堰中考] 如图，小华从点A出发，沿直线前进10m后左转24°，再沿直线前进10m，又向左24°，······，照这样走下去，他第一次回到出发地点A时，一共走的路程是 米.
每个外角都是24°的正多边形.
正好构成一个边长为10米，
且每一个外角都等于24°
解(1)：设这个正多边形的边数为n.
5、正多边形的每个内角可能是：(1)75°；(2)90°；(3)120°吗？说明理由．
∴ 正多边形的每个内角不可能为75°.
6、n边形的各个内角都相等，且它的每一个内角比其外角大108°，求n.
则其每个内角的度数为 (x°+108°）.
设这个多边形的每一个外角的度数为x°，
(x°+108°）+x°=180°
∴ 多边形的边数 n=
7、一个正多边形每一个内角比每一个外角的3倍还大20°，求这个正多边形的内角和.
∴ 这个多边形内角和为
（9-2) ·180°
则其每个内角的度数为 (3x°+20°）.
7、一个正多边形每一个内角比每一个外角的3倍还大20°，求这个正多边形的内角和.
(3x°+20°）+x°=180°
三角形
三角形的各边长确定后，
三角形的形状就确定了.
四边形的各边长确定后，
四边形的形状不能确定
1、在房屋建设过程中，四边形的木质门框容易变形，是因为 ；在实际生活中，木匠师傅通常都是采用在木质门框上斜钉木条的方式来防止门框变形，这样做的道理是 .
必须将四边形转化成三角形.
设这个多边形的每一个内角的度数为x°，
∴ 多边形的一个外角的度数为
∴ 这个多边形每一个内角的度数为
如图，求 ∠A+∠B+∠C+∠D+∠E+∠F 的度数.
∵ ∠1是△BGC的外角
∵ ∠2是△DHE的外角
∴ ∠A+∠B+∠C+∠D+∠E+∠F
=∠A+∠1+∠2+∠F
=(4-2)×180°
再根据多边形的内角和去解决问题.
把分散的角集中到多边形中，
把分散的角集中到多边形中，
如图，求 ∠A+∠B+∠C+∠D+∠E+∠F+∠G 的度数.
∵ ∠A+∠G+∠ANG
=∠BNF+∠ABF+∠GFB
∴ ∠A+∠G=∠ABF+∠GFB
又∵ ∠ANG=∠BNF
∴ ∠A+∠ABC+∠C+∠D+∠E+∠EFG+∠G
=∠ABC+∠C+∠D+∠E+∠EFG+∠ABF+∠GFB
=∠CBF+∠C+∠D+∠E+∠EFB
=(5-2)×180°
利用“8”字型图形的的性质，
如图，试求出∠A＋∠B＋∠C＋∠D＋∠E＋∠F=________.
1、n边形的外角和等于
3、 正n边形的每一个内角
4、 正n边形的每一个外角