沪科版19.2 平行四边形优秀课件ppt

这是一份沪科版19.2 平行四边形优秀课件ppt，共29页。PPT课件主要包含了观察·思考，一组对边，是平行四边形，平行且相等，的四边形，两组对边，分别相等，对角线，互相平分，平行四边形的判定方法等内容，欢迎下载使用。

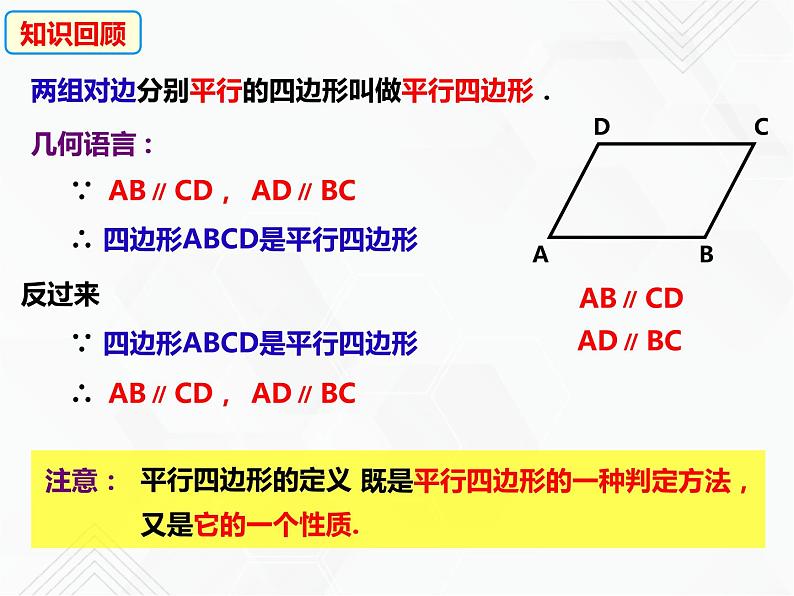
两组对边分别平行的四边形叫做平行四边形．
∴ 四边形ABCD是平行四边形
∵ 四边形ABCD是平行四边形
既是平行四边形的一种判定方法，
平行四边形的对角相等，
平行四边形的性质共有哪些？
如何判断四边形是否是平行四边形呢？
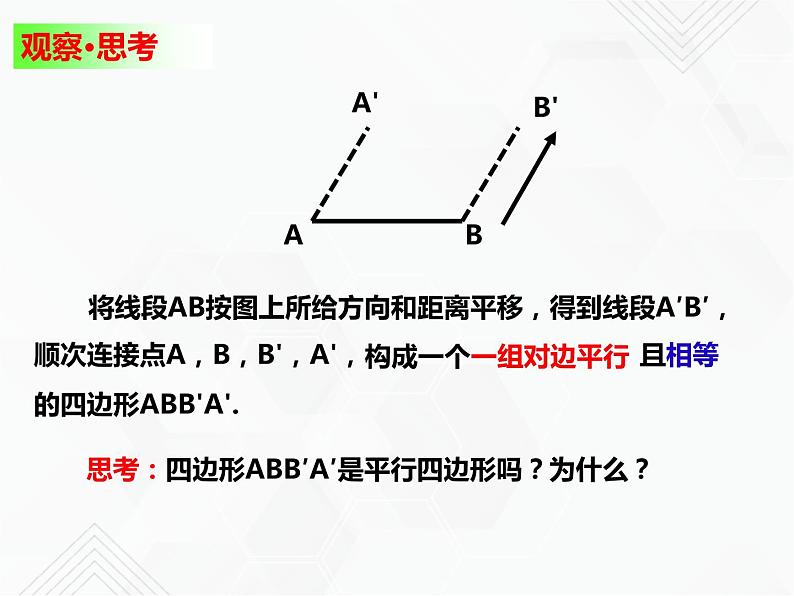
将线段AB按图上所给方向和距离平移，
构成一个一组对边平行
思考：四边形ABB′A′是平行四边形吗？为什么？
顺次连接点A，B，B'，A'，
的四边形ABB'A'.
四边形ABCD为平行四边形.
∴ 四边形ABCD为平行四边形
∴ ∠BAC=∠DCA
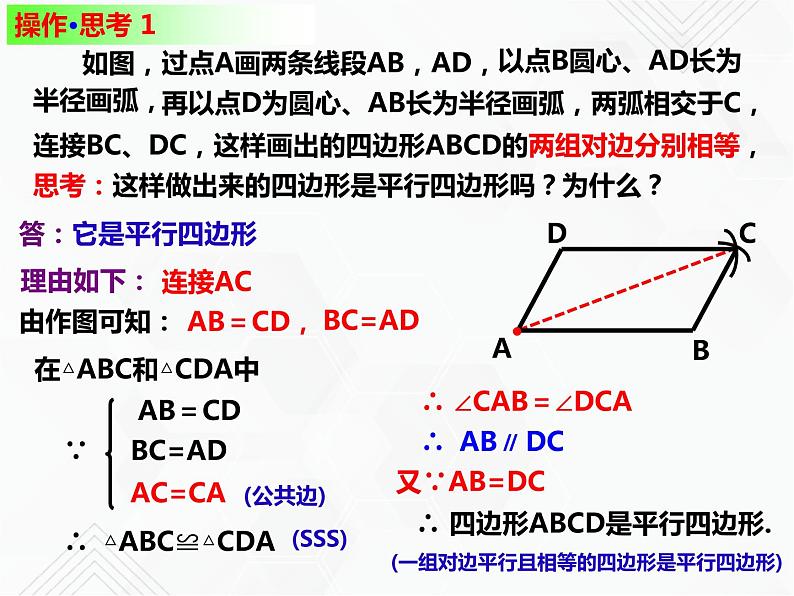
在△ABC和△CDA中
∴ △ABC≌△CDA
∴ ∠ACB=∠CAD
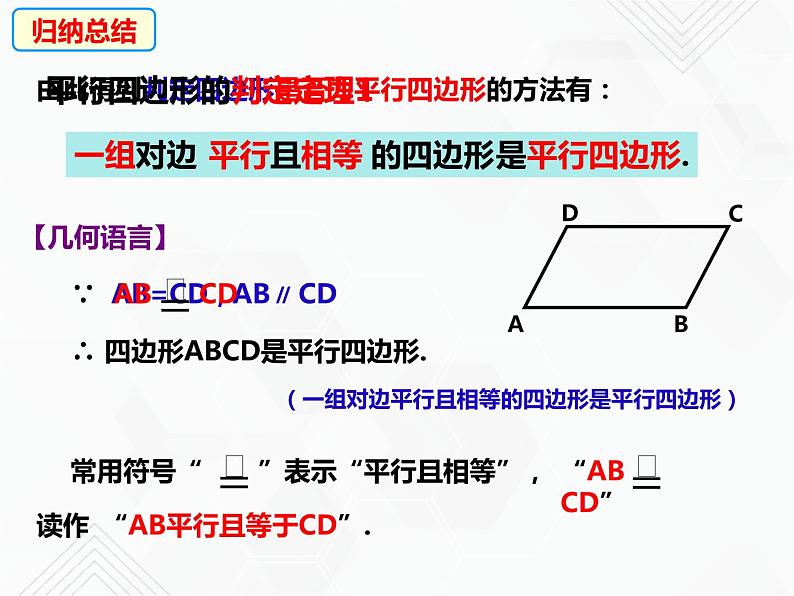
由此得到判定四边形是否为平行四边形的方法有：
∴ 四边形ABCD是平行四边形.
平行四边形的判定定理1
（一组对边平行且相等的四边形是平行四边形）
常用符号“ ”表示“平行且相等”，
“AB CD”
“AB平行且等于CD”.
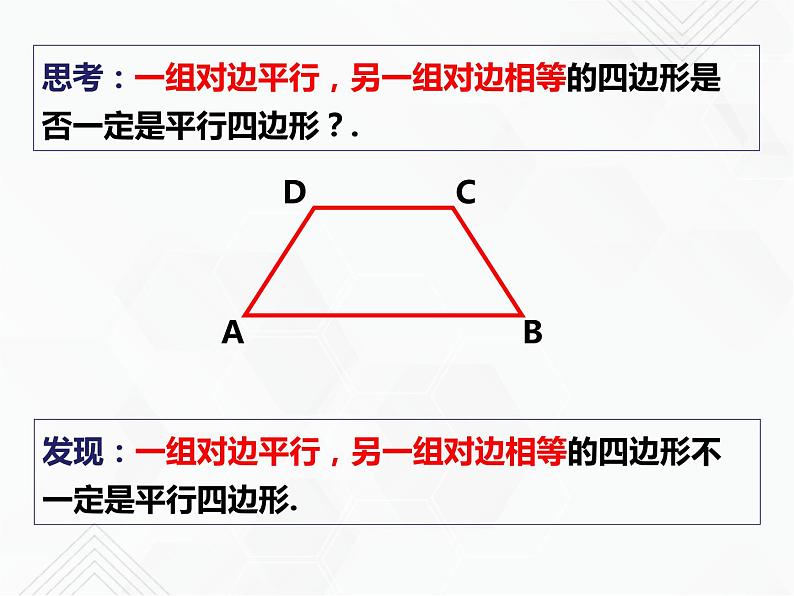
思考：一组对边平行，另一组对边相等的四边形是否一定是平行四边形？.
发现：一组对边平行，另一组对边相等的四边形不一定是平行四边形.
以点B圆心、AD长为半径画弧，
如图，过点A画两条线段AB，AD，
再以点D为圆心、AB长为半径画弧，两弧相交于C，
连接BC、DC，这样画出的四边形ABCD的两组对边分别相等，
思考：这样做出来的四边形是平行四边形吗？为什么？
∴ ∠CAB＝∠DCA
(一组对边平行且相等的四边形是平行四边形)
由此可知，判定四边形为平行四边形的方法还有：
平行四边形的判定定理2
(两组对边分别相等的四边形是平行四边形)
在直线 l1上截取OA＝OC，在直线 l2 上截取OB＝OD，
如图，作两条直线 l1，l2 相交于点O，
连接AB，BC，CD，DA，
这样画出来的四边形ABCD的对角线就互相平分.
思考3：这个四边形是平行四边形吗？为什么？
在△AOB和△COD中
∴ △AOB≌△COD
平行四边形的判定定理3
(对角线互相平分的四边形是平行四边形)
1、根据下列条件,不能判定一个四边形为平行四边形的是( ) (A)两组对边分别相等 (B)两条对角线互相平分 (C)两条对角线相等 (D)两组对边分别平行
2、在下列条件中,不能判定四边形是平行四边形的是( ) AB∥ CD，AD∥BC AB=CD，AD=BC (C) AB∥ CD，AB=CD (D) AB∥CD，AD=BC
(两组对边分别平行的四边形是平行四边形)
（两组对边分别相等的四边形是平行四边形）
3、请你识别下列四边形哪些是平行四边形？为什么？
思考：我们可以从角出发来判定一个四边形是否为平行四边形吗？
已知：四边形ABCD中，∠A=∠C，∠B=∠D.求证：四边形ABCD是平行四边形.
又∵ ∠A=∠C，∠B=∠D
∵ ∠A+∠C+∠B+∠D=360°
∴ 2∠A+2∠B=360°
即 ∠A+∠B=180°
∴ ∠A+∠D=180°.
两组对角分别相等的四边形也是平行四边形
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
(平行四边形的定义)
两组对边分别相等的四边形是平行四边形
对应练习 填空：如图在四边形ABCD中
(1) 若AB//CD，补充条件 ，使四边形ABCD为平行四边形； (2) 若AB=CD，补充条件 使四边形ABCD为平行四边形； (3)若对角线AC、BD交于点O，OA=OC=3，OB=5，补充条件 ，使四边形ABCD为平行四边形.
判定平行四边形的证明思路：
② 证明另一组对边也相等
① 证明另一组对边也平行
证明另一组对角也相等
1、已知：如图，点E，F是 ABCD的对角线AC上两点，且 AE＝CF，求证：四边形BEDF是平行四边形.
∴ OA - AE＝OC - CF
∴ 四边形BEDF是平行四边形
2、如图，E，F是四边形ABCD的对角线AC上两点，AF＝CE，DF＝BE，DF∥ BE，求证：四边形ABCD是平行四边形.
∴ ∠DFE＝∠BEF
∴ ∠AFD＝∠CEB
∴ △AFD≌△CEB
∴ ∠DAC＝∠BCA，
在△ADF和△CBE中
3、如图，在 ABCD中，BN=DM，BE=DF. 求证：四边形MENF是平行四边形.
∴ ∠NBE=∠MDF
在△BNE和△DME中
∴ △BNE≌△DME
∴ ∠NEF=∠MFE
∴ 四边形MENF是平行四边形
4、画□ ABCD，使AB＝2cm，BC＝3cm，AC＝4cm．
① 用直尺画2cm的线段AB
② 用圆规以A为圆心，
③ 连接AC，BC，
再以B为圆心3cm为半径画弧，
5、 如图，在平行四边形ABCD中，已知AE、CF分别是∠DAB、∠BCD的角平分线，试证明四边形AFCE是平行四边形．
∵ 在平行四边形ABCD中
∵ AE、CF分别是∠DAB,∠BCD的角平分线
在△ABE和△CDF中
∴ ∠BAE=∠DCF
∴四边形AFCE是平行四边形
∴ △ABE≌△CDF
6、如图，四边形ABCD是平行四边形，E，F是对角线BD上的点，∠1＝∠2.求证： AF∥ CE.
∴ ∠AEB＝∠DFC
∴ 四边形AECF是平行四边形