沪科版八年级下册第19章 四边形19.4 综合与实践 多边形的镶嵌优质课ppt课件

这是一份沪科版八年级下册第19章 四边形19.4 综合与实践 多边形的镶嵌优质课ppt课件，共36页。PPT课件主要包含了四边形中，生活中处处有数学，平移对角线，平移一腰，作高线，延长两腰，转化思想，本节课你有什么收获等内容，欢迎下载使用。

几种特殊四边形的定义及性质：
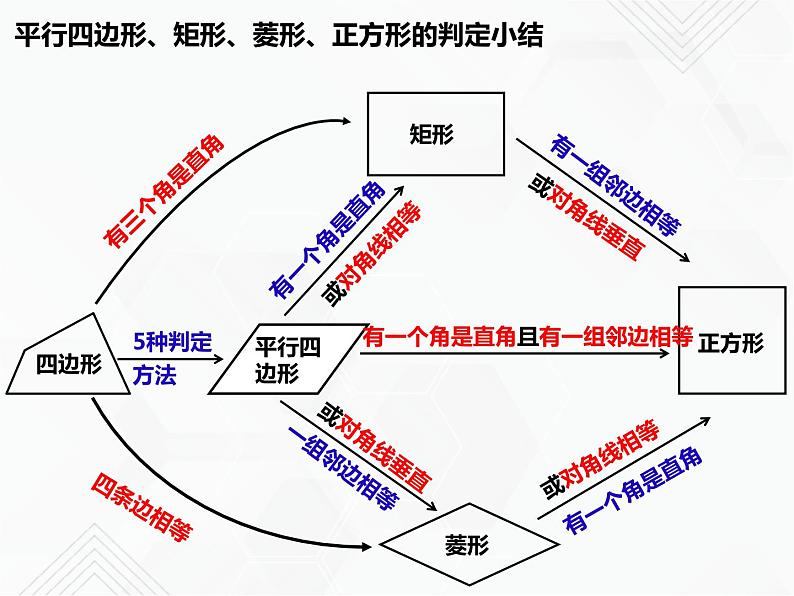
两组对边分别平行的四边形
有一个角是直角的平行四边形
有一组邻边相等的平行四边形
对边平行且四条边都相等
对角线互相垂直平分，并且每条对角线平分一组对角
有一组邻边相等且有一个角是直角的平行四边形
对角线相等且互相垂直平分，并且每条对角线平分一组对角
有一个角是直角且有一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
我们研究了其中一类特殊的四边形——
今天我们来研究另一类四边形.
两组对边分别平行的四边形.

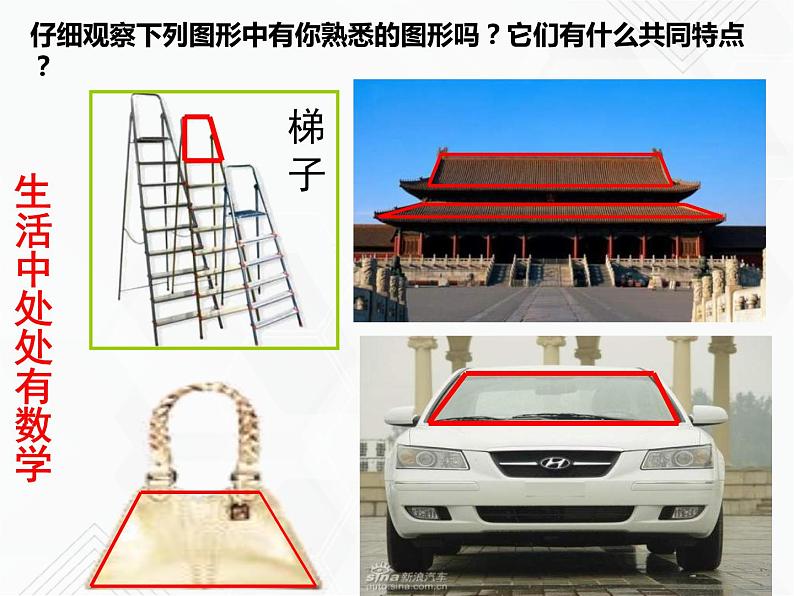
仔细观察下列图形中有你熟悉的图形吗？它们有什么共同特点？
上海世博会中国馆——东方之冠
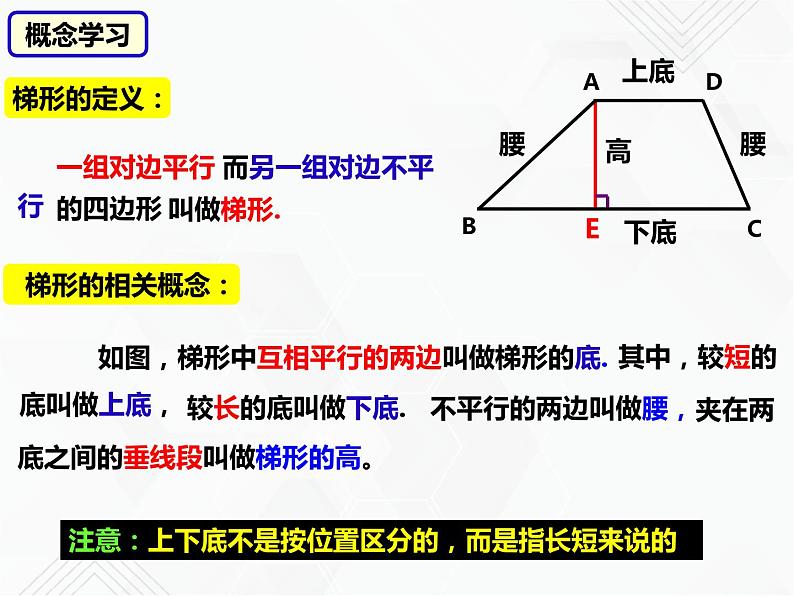
夹在两底之间的垂线段叫做梯形的高。
其中，较短的底叫做上底，
如图，梯形中互相平行的两边叫做梯形的底.
不平行的两边叫做腰，
注意：上下底不是按位置区分的，而是指长短来说的
而另一组对边不平行
有一个角是直角的梯形叫做直角梯形
两腰相等的梯形叫做等腰梯形
观察思考：下面的图形是轴对称图形吗？如果是，有几条对称轴？
对称轴是上下底中点所在直线.
等腰梯形是轴对称图形，
等腰梯形有哪些性质呢
等腰梯形同一底边上的两个角相等.
等腰梯形对角线相等.
等腰梯形同一腰上的两个角互补.
证明：过点D作DE∥ AB,交BC于点E ∴ ∠DEC=∠B 又∵ AD∥ BC　 ∴ 四边形ABED是平行四边形 ∴ AB = DE 又∵ AB=DC ∴ DE=DC ∴ ∠DEC=∠C ∴ ∠B=∠C
已知，梯形ABCD中，AD//BC，且AB=CD
求证：∠B=∠C，∠A=∠D
又∵∠B+∠A=180°，∠C+∠ADC=180°
法二： 过点A作AE⊥BC于点E， 过点D作DF⊥BC于点F
证明Rt△ABE与Rt△DCF全等
已知：梯形ABCD中，AD//BC，且AB=CD
∴ △ABC≌△DCB
∴ ∠ ABC=∠DCB
∴ 在△ABC与△DCB中
∠ ABC=∠DCB
2、一个三角形有几条中位线？
1、什么是三角形的中位线？
3、什么是三角形中位线定理？
∵ DE是△ABC的中位线
(或 AD=BD，AE=CE)
连接梯形两腰中点的线段
注意：梯形有 条中位线,而三角形有 条.
如图，EF是梯形ABCD的中位线. 猜想一下EF与梯形的两底边AD，BC有怎样的位置关系和数量关系?
已知：如图，在梯形ABCD中，AD ∥ BC，AE＝EB，DF＝FC
求证：EF∥ AD∥ BC，EF＝ (AD＋BC)
∴ ∠DAF=∠CGF,
∴ 在△DAF与△CGF中
∴ △DAF≌△CGF
∴ EF是△ABE的中位线
∴ EF∥ BC ∥ AD，
并延长与BC的延长线交于点G
EF= (AD+BC)
并且等于两底和的一半.
∵ EF是梯形ABCD的中位线
∴EF∥ AD∥ BC，
S梯形 =
1、在梯形ABCD中，AD∥ BC，∠A：∠B：∠C：∠D可以是（ ） （A）4：3：1：2 （B）4：2：3：1 （C）4：1：3：2 （D）不能确定
2、如图，在等腰梯形ABCD中，AD∥ BC，BD⊥DC于D， ∠C=60°，若AD=5，则BC= 。
3、一等腰梯形的腰长为13cm，两底差为10cm，则其高为（ ） （A）69cm （B）12cm （C）144cm （D）25cm
证明 : ∵ 四边形ABCD是等腰梯形
∴ △EBC是等腰三角形
∴ ∠EAD=∠B，∠EDA=∠C
∴ ∠EAD＝∠EDA∴ AE=DE
∴ △EAD是等腰三角形.
延 长 两 腰
4、如图：延长等腰梯形ABCD的两腰BA和CD，相交于点E.求证:△EBC和△EAD都是等腰三角形.
5、如图，在等腰梯形ABCD中，AB//DC，CE//DA，已知AB=8，DC=5，DA=6. △CEB的周长.
解 : ∵ 四边形ABCD是等腰梯形 ∴ AD=BC=6
∴ 四边形AECD是平行四边形.
∵ AD//CE，CD//AB
∴ △CEB的周长=EB+CE+BC=3+6+6=15.
① 一个梯形的上底长4 cm，下底长6 cm，则其中位线长为 cm； ② 一个梯形的上底长10 cm，中位线长16 cm，则其下底长为 cm； ③ 已知梯形的中位线长为6 cm，高为8 cm，则该梯形的面积为________ cm2 ； ④ 已知等腰梯形的周长为80 cm，中位线与腰长相等，则它的中位线长 cm；
7、如图，梯形ABCD的周长为20，AB∥ CD，AM、BN分别是∠DAB 、∠ABC的外角平分线，DM⊥AM于M，CN⊥BN于N，求线段MN的长.
8、如图，在梯形ABCD中，AD∥ BC，对角线AC⊥BD，且AC＝12，BD＝9，则此梯形的中位线长是（ ） A．10　 　B．　　 C．　　 D．12
9、如图所示的梯形ABCD中，AD∥ BC，对角线AC与BD垂直相交于O，MN是中位线，∠DBC=30°，求证：AC=MN.
10、如图所示，在梯形ABCD中，AD∥ BC，AD=2，BC=8，AC=6，BD=8，求梯形的面积.
12、如图，梯形ABCD中，M，N分别是对角线BD，AC的中点. 求证：MN∥ BC，MN= (BC-AD).
解决梯形问题的常用辅助线