






- 14.5 一次函数的图象 课件 课件 3 次下载
- 14.7 一次函数的应用 课件 课件 3 次下载
- 14.7一次函数的应用_课件1 课件 4 次下载
- 14.4一次函数_课件1 课件 4 次下载
- 14.2函数的表示法_课件1 课件 3 次下载
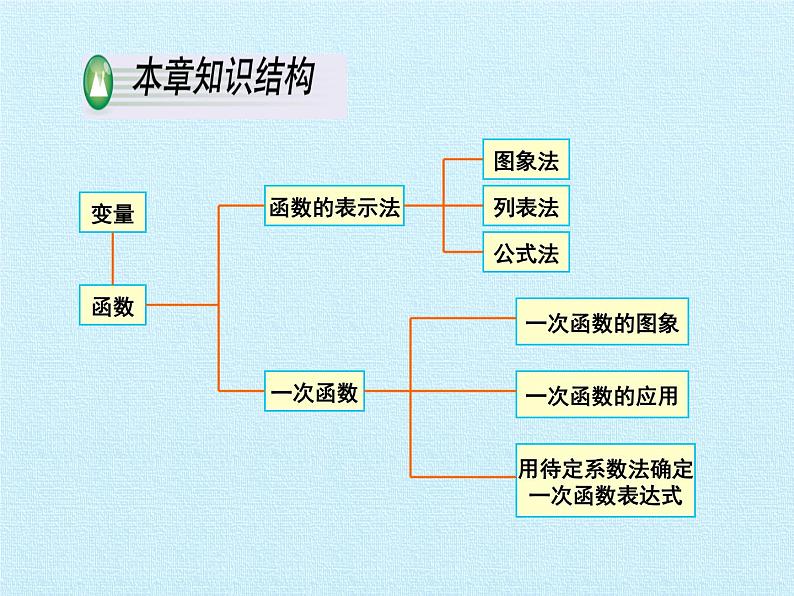
北京课改版八年级下册14.4 一次函数复习课件ppt
展开取值会发生变化的量称为变量
取值固定不变的量称为常量(或常数)
如果变量 y 随着变量 x 而变化,并且对于 x 取得的每一个值,y 都有唯一的一个值与它对应,那么称 y是x 的函数记作y =f (x).
这时把 x 叫作自变量,把 y 叫作因变量
对于自变量 取的每一个值a,因变量y的对应值称为函数值记作f (a).
建立一个平面直角坐标系,以自变量取的每一个值为横坐标,以相应的函数值(即因变量的对应值)为纵坐标,描出每一个点,由所有这些点组成的图形成为这个函数的图像. 这种表示函数关系的方法称为图像法.
用图象法表示函数关系的好处是,可以直观地看出因变量如何随着自变量而变化,一目了然.
反过来,以满足函数关系式的有序数对为坐标的点都在函数的图象上.
函数图象上的点的坐标都满足函数关系式.
画函数图象的方法是描点法,其一般步骤:(1)列表;(2)描点;(3)连线.
函数的图象可以是直线或曲线,还可以是由一些点或一些线段组成的图形.
列一张表,第一行表示自变量取的各个值,第二行表示相应的函数值,(即因变量的对应值). 这种表示函数关系的方法称为列表法.
用列表法表示函数关系的好处是,自变量取的值与因变量的对应值看得很清楚.
用式子表示函数关系的方法称为公式法,这样的式子称为函数解析式
用公式法表示函数关系的好处是,可以方便地计算函数值.
函数解析式的一般形式是:
因变量=关于自变量的代数式
同时注明自变量的取值范围
如果函数的解析式是自变量的一次式,那么这样的函数称为一次函数,它的一般形式是 y = kx+b,其中 k≠0 特别地,当b=0时,一次函数y = kx (k≠0) 也叫做正比例函数.
画出正比例函数y=kx(k≠0)的图象的步骤:
(1)先选取两点,通常选点(0,0)与点(1,k);
(2)在坐标平面内描点(0,0)与点(1,k);
(3)过点(0,0)与点(1,k)画一条直线。
这条直线就是正比例函数y=kx(k≠0)的图象。
正比例函数y=kx有下列性质:
(1)当k>0时,图象经过一、三象限,y随着x的增大(减小)而增大(减小)
(2)当k<0时,图象经过二、四象限,y随着x的增大(减小)而减小(增大)
正比例函数y=kx(k≠0)的图象和性质:
一次函数y= kx+b(k≠0)的图像是一条直线. 由于两点确定一条直线,因此画一次函数的图像,只要描出图像上的两个点,然后过这两点作一条直线就行了. 常常把这条直线叫作“直线y=kx+b”.
画出一次函数y=kx+b(k≠0)的图象的步骤:
(1)先选取两点,通常选点(0,b)与点( ,0);
(2)在坐标平面内描点(0,b)与点( ,0);
(3)过点(0,b)与点( ,0)画一条直线.
这条直线就是一次函数y=kx+b(k≠0)的图象.
在一次函数y=kx+b中k的符号决定直线的倾斜程度b的符号决定直线与y轴的交点的位置
一次函数y=kx+b(k≠0)中k、b的作用
2、当k1=k2时,直线y=k1x+b1和y=k2x+b2平行.
当k1≠k2时,直线y=k1x+b1和y=k2x+b2相交.
1、求直线y=kx+b与x轴、y轴交点的方法:令x=0,y=b,得直线y轴的交点坐标(0,b)令y=0,x= 得直线x轴的交点坐标( ,0)
判断是否为一次函数模型的关键是因变量是否随自变量均匀的变化或看函数图象是否为直线型.(直线、射线、线段,成直线形状的孤立点)
通过确定函数模型,然后列方程组求待定系数,从而求出函数的解析式,这种方法叫待定系数法.
(1)设函数表达式y=kx+b(2)根据已知条件列出关于k,b的方程(组)(3)解方程(组)(4)把求出的k,b值代回到表达式中即可
待定系数法求一次函数解析式的步骤:
(3,1)或(1,4)等
人教版八年级下册第十九章 一次函数综合与测试复习ppt课件: 这是一份人教版八年级下册第十九章 一次函数综合与测试复习ppt课件,共16页。PPT课件主要包含了基础知识,拓展解析,∴此函数为正比例函数,∴k2,∴k≠±2,≤a5,第二象限,或原点,知识点补充,∴k-2等内容,欢迎下载使用。
初中数学第十九章 一次函数综合与测试复习ppt课件: 这是一份初中数学第十九章 一次函数综合与测试复习ppt课件,共23页。
初中数学人教版八年级下册第十九章 一次函数综合与测试复习ppt课件: 这是一份初中数学人教版八年级下册第十九章 一次函数综合与测试复习ppt课件,共17页。PPT课件主要包含了知识梳理,合作探究,综合应用小训练,整理归纳,从数到形,从形到数等内容,欢迎下载使用。













