




初中数学沪科版九年级下册24.1.3 中心对称图形完美版备课ppt课件
展开下列各点分别在坐标平面的什么位置上?
A(3,2)B(0,-2)C(-3,-2)D(-3,0)E(-1.5,3.5)F(2,-3)
24.1.3 图形在平面直角坐标系中的变换
问题:2016年里约热内卢奥运会会徽是由三人牵手相连的标志,以代表巴西的著名景点“面包山”作为图形的基础,融合充满激情的卡里奥克舞,并且呼应了巴西国旗的绿黄蓝三色.说一说图案中的奥运五环可以通过其中一个圆怎样变化而得到?
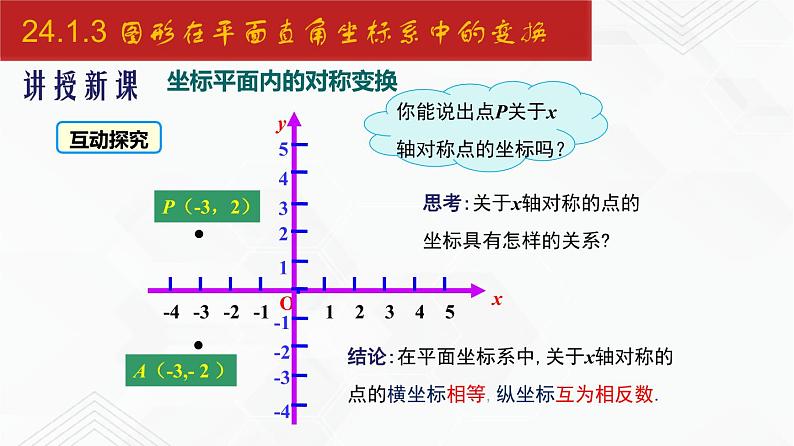
A(-3,- 2 )
思考:关于x轴对称的点的坐标具有怎样的关系?
结论:在平面坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数.
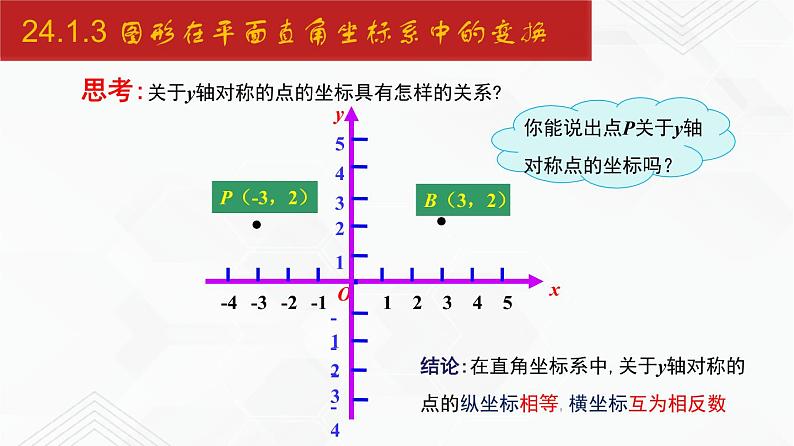
思考:关于y轴对称的点的坐标具有怎样的关系?
结论:在直角坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数
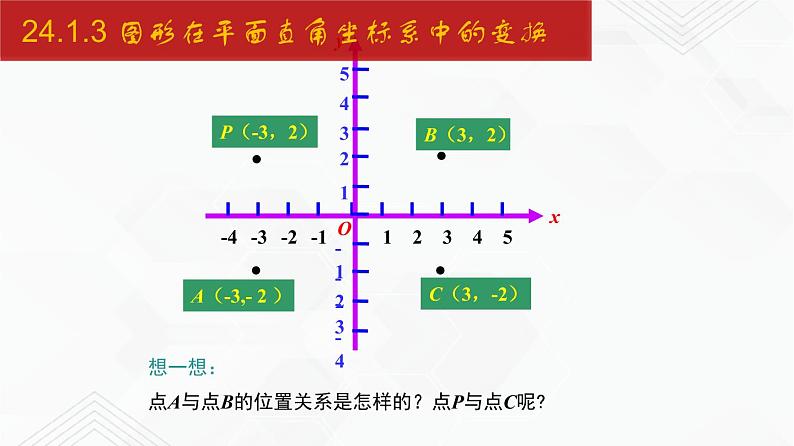
想一想:点A与点B的位置关系是怎样的?点P与点C呢?
简记为:“关于谁,谁不变,关于原点都改变”.
点P(a,b)关于原点对称的点的坐标为P′(-a,-b);点P(a,b)关于x轴对称的点的坐标为P′(a,-b);点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
例1 填空:(1)在平面直角坐标系中,点P(2,-3)关于原点对称的点P′的坐标是________.(2)点P(2,n)与点Q(m,-3)关于原点对称,则(m+n)2015=________.(3)点M(3,-5)绕原点旋转180°后到达的位置是________.
解析:(1)因为点P(2,-3)与点P′关于原点对称,所以点P′的坐标是P′(-2,3).(2)因为点P(2,n)与点Q(m,-3)关于原点对称,所以m=-2,n=3,则(m+n)2015=(-2+3)2015=1.(3)因为点M(3,-5)绕原点旋转180°后到达的位置与原来的点关于原点对称,所以到达的位置是(-3,5).
已知点A(2a+2,3-3b)与点B(2b-4,3a+6)关于坐标原点对称,求a与b的值.
例2 如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
解:△ABC的三个顶点 A(-4,1),B(-1, -1),C(-3,2)
A′(4,-1),B′(1,1),C′(3,-2)
关于原点的对称点分别为
依次连接A ′B ′ ,B ′ C ′ ,C ′ A ′ ,就可得到与△ABC关于原点对称的△ A′B′ C ′ .
(1)写出图形顶点坐标; (2)写出图形顶点关于原点的对称点的坐标; (3)描点; (4)顺次连接; (5)下结论.
作关于原点对称的图形的步骤:
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
(1)分别画出△ABC以点O(0,0)为旋转中心,在图(1)中旋转90°、在图(2)中旋转180°、在图(3)中旋转270°、在图(4)中旋转360°而得到的△A′B′C′;
(2)给出点A′,B′,C′的坐标(填在下表中):
思考:分别比较点A′与点A、点B′与点B、点C′与点C的坐标,能得到怎样的结论?
通过作图、分析能看到,把一个图形以点O为旋转中心作几个特殊角度的旋转,可得如下结果:
这里,把(x,y)变换成(x,y)的变换叫做恒等变换,即在平面直角坐标系中,一个图形绕点O作360°旋转是一个恒等变换.
试说出构成下列图形的基本图形.
想一想:看成轴对称时基本图形是什么?
图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案.
例3 下面花边中的图案以正方形为基础,由圆弧、圆或线段构成.仿照例图,请你为班级的板报设计一条花边.要求:(1)只要画出组成花边的一个图案;(2)以所给的正方形为基础,用圆弧、圆或线段画出;(3)图案应有美感.
你能找出图案中的全等图形吗?
这幅图案可看成是怎样制作的呢?
★★★ ★★★ ★★★★★ ★★★★★ ★★★★★★★★★★★ ★★★★★★★★★ ★★★★★★★ ★★★★★ ★★★ ★
祝同学们学习快乐天天开心
1.下列各点中哪两个点关于原点O对称? A(-5,0) B(0,2) C(2,-1) D(2,0) E(0,5) F(-2,1) G(-2,-1)2.写出下列各点关于原点的对称点的坐标. A(3,1) B(-2,3) C(-1,-2) D(2,-3)
A(-3,-1) B(2,-3) C(1,2) D(-2,3)
3.若点A(m,-2),B(1,n)关于原点对称,则m=_____,n=_____ .
4.在如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为________.
5.已知a<0,则点P(-a2,-a+1)关于原点的对称点P′在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限
解析:∵点P(-a2,-a+1)关于原点的对称点P′(a2,a-1),∵a<0,∴a2>0,-a+1<0,∴点P′在第四象限,故选D.
6.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )A.(2,5)B.(5,2)C.(2,-5)D.(5,-2)
7.已知:如图,E(-4,2),F(-1,-1),以O为中心,把△EFO旋转180°,则点E的对应点E′的坐标为(_____________).
8.如图,已知A的坐标为( ,2),点B的坐标为(-1, ),菱形ABCD的对角线交于坐标原点O.求C,D两点的坐标.
2.在平面直角坐标系中,以原点为旋转中心把一个图形按逆时针方向旋转,原图上任意一点坐标(x,y)旋转特定角度后对应点的坐标如下表:
3.把(x,y)变换成__________的变换叫做恒等变换.
1.点P(a,b)关于原点对称的点的坐标为P′(-a,-b);点P(a,b)关于x轴对称的点的坐标为P′(a,-b);点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
数学沪科版22.4 图形的位似变换精品教学课件ppt: 这是一份数学沪科版22.4 图形的位似变换精品教学课件ppt,共15页。PPT课件主要包含了学习目标,导入新课,讲授新课,合作探究,当堂练习,-10等内容,欢迎下载使用。
初中数学沪科版九年级上册22.4 图形的位似变换多媒体教学课件ppt: 这是一份初中数学沪科版九年级上册22.4 图形的位似变换多媒体教学课件ppt,共31页。PPT课件主要包含了学习目标,导入新课,复习引入,位似图形,位似中心,相似比或位似比,平行或者在一条直线上,基本模型,讲授新课,合作探究等内容,欢迎下载使用。
数学26.4 概率在遗传学中的应用精品备课课件ppt: 这是一份数学26.4 概率在遗传学中的应用精品备课课件ppt,共30页。PPT课件主要包含了孟德尔等内容,欢迎下载使用。













