数学九年级下册24.3.1 圆周角定理精品备课课件ppt

这是一份数学九年级下册24.3.1 圆周角定理精品备课课件ppt，共30页。PPT课件主要包含了31圆周角，讲授新课，课堂小结等内容，欢迎下载使用。
3.下列命题是真命题的是( )①在同圆中，相等的弦所对的圆心角相等；②相等的圆心角所对的弧相等③圆既是轴对称图形,又是中心对称图形A.①② B.①③ C.②③ D.①②③
答:顶点在圆心的角叫圆心角.
2.圆心角的度数和它所对的弧的度数的关系?
如图是一个圆柱形的海洋馆的横截面示意图,人们可以通过其中的圆弧形玻璃窗观看窗内的海洋动物,同学甲站在圆心O的位置，同学乙站在正对着玻璃窗的靠墙的位置C，他们的视角(∠AOB和∠ACB)有什么关系?如果同学丙、丁分别站在其他靠墙的位置D和E，他们的视角（ ∠ADB和∠AEB）和同学乙的视角相同吗？
观察图中∠ACB、∠ADB和∠AEB与我们学过的圆心角有什么区别？
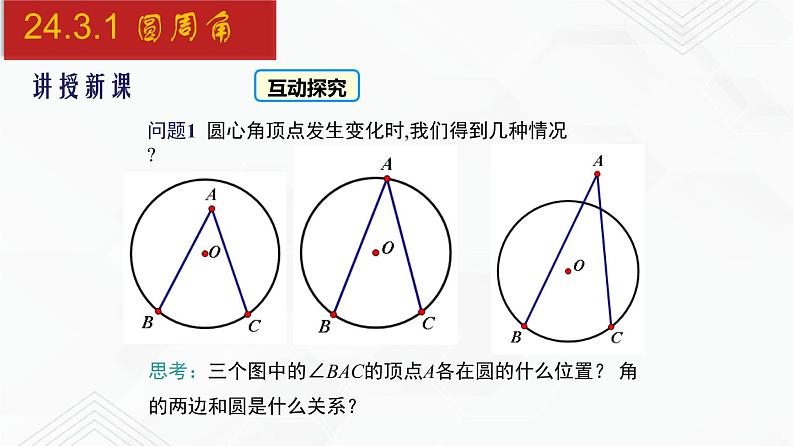
问题1 圆心角顶点发生变化时,我们得到几种情况?
思考：三个图中的∠BAC的顶点A各在圆的什么位置？ 角的两边和圆是什么关系？
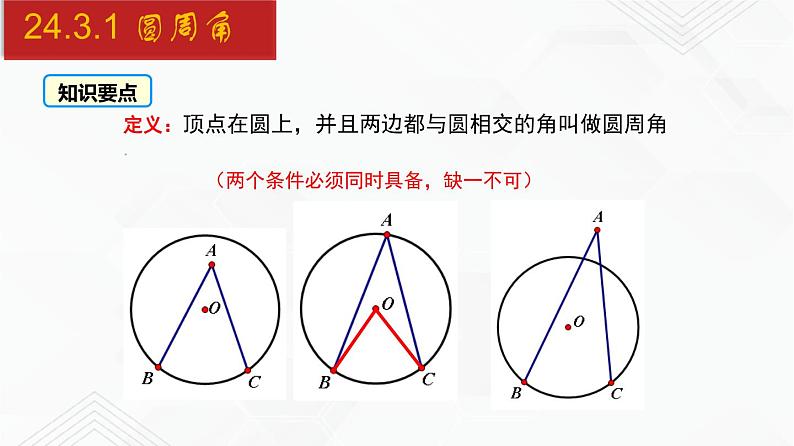
定义：顶点在圆上，并且两边都与圆相交的角叫做圆周角.
（两个条件必须同时具备，缺一不可）
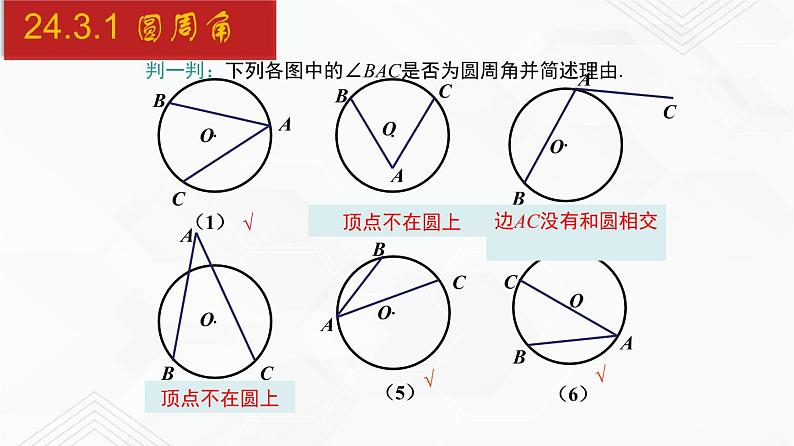
判一判：下列各图中的∠BAC是否为圆周角并简述理由.
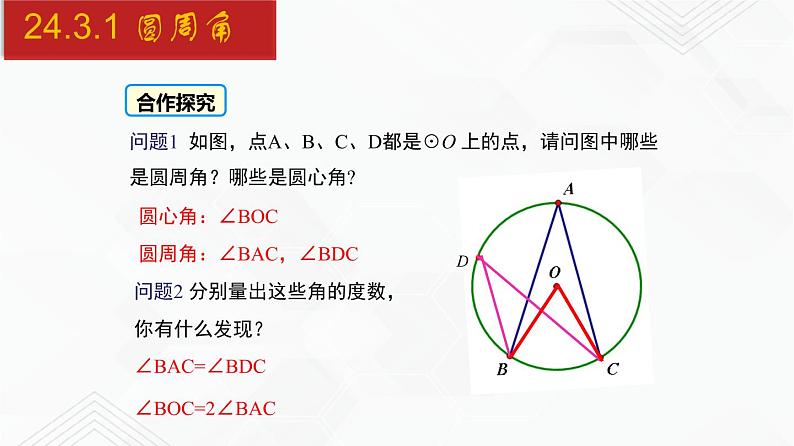
问题1 如图，点A、B、C、D都是☉O 上的点，请问图中哪些是圆周角？哪些是圆心角?
圆周角：∠BAC，∠BDC
问题2 分别量出这些角的度数，你有什么发现？
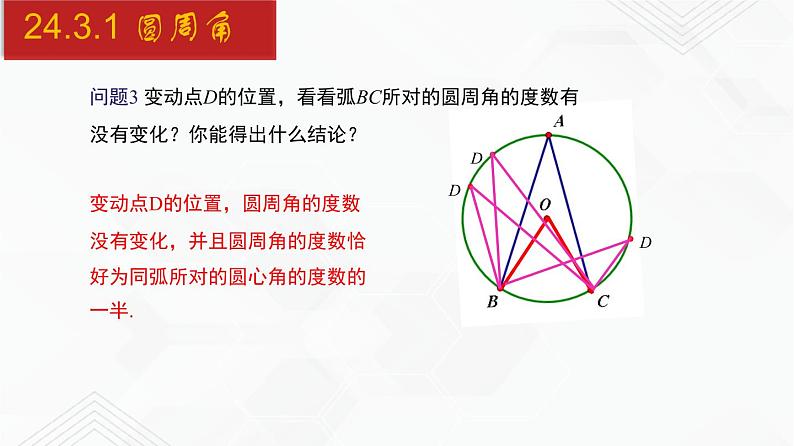
问题3 变动点D的位置，看看弧BC所对的圆周角的度数有没有变化？你能得出什么结论？
变动点D的位置，圆周角的度数没有变化，并且圆周角的度数恰好为同弧所对的圆心角的度数的一半.
圆心O在∠BAC的内部
圆心O在∠BAC的一边上
圆心O在∠BAC的外部
圆心O在∠BAC的一边上（特殊情形）
∠BOC= ∠ A+ ∠C
一条弧所对的圆周角等于它所对的圆心角的一半.
如图，点A，B，C是☉O 上的点，连接AB，AC，OB，OC，则
∴∠ACB=2∠BAC
例1 如图，OA，OB，OC都是⊙O的半径，∠AOB=2∠BOC. 求证：∠ACB=2∠BAC.
∠AOB=2∠BOC，
问题1 如图，OB，OC都是⊙O的半径，点A ,D 是上任意两点，连接AB，AC，BD，CD.∠BAC与∠BDC相等吗？请说明理由.
(2)若CD是直径，你能求出∠A的度数吗？
推论1 在同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等.
推论2：半圆或直径所对的圆周角是直角；90°的圆周角所对的弦是直径.
∵ AB是直径∴∠AC1B=90°
∵ ∠AC1B=90°∴ AB是直径.
例2 如图,AB是⊙O的直径,弦CD交AB于点P,∠ACD=60°,∠ADC=70°.求∠APC的度数.
解:连接BC,则∠ACB=90°,
∠DCB＝∠ACB－∠ACD＝90°－60°=30°.
又∵∠BAD=∠DCB=30°,
∴∠APC=∠BAD＋∠ADC＝30°＋70°＝100°.
例3 如图，☉O直径AC为10cm，弦AD为6cm. （1）求DC的长；
（2）若∠ADC的平分线交☉O于B, 求AB、BC的长．
解：(1)∵AC是直径，
∴ ∠ADC=90°.
在Rt△ABC中，AB2+BC2=AC2，
(2)∵ AC是直径, ∴ ∠ABC=90°. ∵BD平分∠ADC, ∴∠ADB=∠CDB.又∵∠ACB=∠ADB , ∠BAC=∠BDC . ∴ ∠BAC=∠ACB, ∴AB=BC.
解答圆周角有关问题时，若题中出现“直径”这个条件，通常考虑构造直角三角形来求解.
1.判断（1）同一个圆中等弧所对的圆周角相等 （ ）（2）相等的弦所对的圆周角也相等 （ ）（3）900的角所对的弦是直径 （ ）（4）同弦所对的圆周角相等 （ ）
2.如图，AB是☉O的直径, C 、D是圆上的两点,∠ABD=40°,则∠BCD=＿＿＿_.
3.已知△ABC的三个顶点在☉O上,∠BAC=50°,∠ABC=47°,则∠AOB= ．
4.如图，点B，C在⊙O上，且BO=BC，则圆周角∠BAC等于（ ）
4.如图，已知BD是⊙O的直径，⊙O的弦AC⊥BD于点E，若∠AOD=60°，则∠DBC的度数为（ ） A.30° B.40° C.50° D.60°
【规律方法】解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.
如图，分别求出图中∠x的大小.
解：(1)∵同弧所对圆周角相等，∴∠x=60°.
∵同弧所对圆周角相等，
∴∠ABF=∠D=20°，∠FBC=∠E=30°.
∴∠x=∠ABF+∠FBC=50°.
∵AB是圆的直径，点D在圆上，
∴BD=CD,AD平分顶角∠BAC，即∠BAD=∠CAD，
（同圆或等圆中相等的圆周角所对弧相等）.
解:BD=CD.理由是:连接AD,
1.顶点在圆上；2.两边都与圆相交的角
半圆或直径所对的圆周角是直角；90°的圆周角所对的弦是直径.
在同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等.