初中数学华师大版八年级下册第18章 平行四边形综合与测试同步练习题

这是一份初中数学华师大版八年级下册第18章 平行四边形综合与测试同步练习题，共26页。

此套题为Wrd版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。关闭Wrd文档返回原板块。


第18章单元达标检测试卷


[时间：90分钟 分值：150分]


一、选择题(每题3分，共30分)


1．下列说法不正确的是( )


A．平行四边形的对边平行


B．两组对边分别平行的四边形是平行四边形


C．平行四边形的对角相等


D．一组对角相等的四边形是平行四边形


2．如图，在▱ABCD中，∠B＝110°，延长AD至点F，延长CD至点E，连结EF，则∠E＋∠F等于( )





A．110° B．30° C．50° D．70°








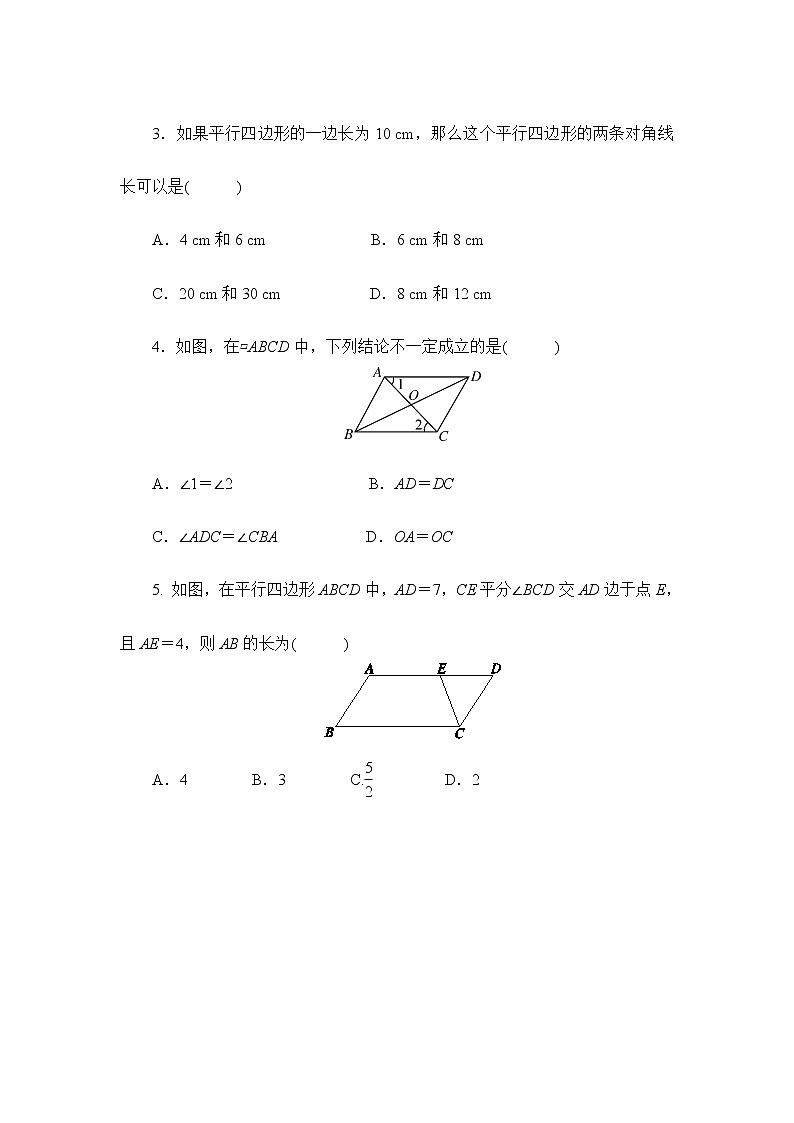
3．如果平行四边形的一边长为10 cm，那么这个平行四边形的两条对角线长可以是( )


A．4 cm和6 cm B．6 cm和8 cm


C．20 cm和30 cm D．8 cm和12 cm


4．如图，在▱ABCD中，下列结论不一定成立的是( )





A．∠1＝∠2 B．AD＝DC


C．∠ADC＝∠CBA D．OA＝OC


5. 如图，在平行四边形ABCD中，AD＝7，CE平分∠BCD交AD边于点E，且AE＝4，则AB的长为( )





A．4 B．3 C.eq \f(5,2) D．2























6．如图，▱ABCD的对角线相交于点O，AO＝4，OD＝7，△DBC的周长比△ABC的周长( )


A．长6 B．短6 C．短3 D．长3











7．如图，在▱ABCD中，∠ODA＝90°，AC＝10 cm，BD＝6 cm，则AD的长为( )





A．4 cm B．5 cm C．6 cm D．8 cm











8．如图，在平行四边形ABCD中，E、F分别是边BC、AD上的点，有下列条件：


①AE∥CF；②BE＝FD；③∠1＝∠2；④AE＝CF.


若要添加其中一个条件，使四边形AECF一定是平行四边形，则添加的条件可以是( )








A．①②③④


B．①②③


C．②③④


D．①③④


9．如图，在▱ABCD中，M是CD的中点，AB＝2BC，BM＝1，AM＝2，则CD的长为( )





A.eq \f(5,2) B．2 C.eq \r(2) D.eq \r(5)





10．如图，在四边形ABCD中，AB＝CD，对角线AC、BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连结AF、CE.若DE＝BF.下列结论：①CF＝AE；②OE＝OF；③四边形ABCD是平行四边形；④图中共有四对全等三角形．其中正确结论的个数是( )





A．4 B．3 C．2 D．1





二、填空题(每题4分，共24分)


11．如图，在▱ABCD中，AC、BD相交于点O.若AD＝6，AC＋BD＝16，则△BOC 的周长为 ．














12．在如图所示的▱ABCD中，AB＝2，AD＝3，将△ACD沿对角线AC折叠，点D落在△ABC所在平面内的点E处，且AE过BC的中点O，则△ADE的周长等于 ．





13．如图，在▱ABCD中，AB＝6，BC＝8，∠C的平分线交AD于点E，交BA的延长线于点F，则AE＋AF的值等于 ．





14．如图，在▱ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA.若AD＝5，AP＝8，则△APB的周长是 ．

















15．如图，点A、E、F、C在一条直线上，若将△DEC的边EC沿AC方向平移，平移过程中始终满足下列条件：AE＝CF，DE⊥AC于点E，BF⊥AC于点F，且AB＝CD，则当点E、F不重合时，BD与EF的关系是 ．








16．如图，在▱ABCD中，AD＝8 cm，AB＝4 cm，AE平分∠BAD交BC边于点E，交DC的延长线于点F，则下列结论：①CE＝4 cm; ②线段AF、BC互相平分； ③AC⊥DF；④DE⊥AF.其中正确的结论是 (填序号)．




















三、解答题(共66分)


17．(8分)如图，在▱ABCD中，E为BC边上一点，且∠B＝∠AEB.求证：AC＝DE.























18．(10分)如图，AB∥CD，AB＝CD，点B、E、F、D在同一条直线上，∠BAE＝∠DCF.


(1)求证：AE＝CF；


(2)连结AF、EC，试猜想四边形AECF是什么四边形，并证明你的结论．




















19．(10分)如图，在▱ABCD中，点E在边BC上，点F在边DA的延长线上，且AF＝CE，EF与AB交于点G.


(1)求证：AC∥EF；


(2)若点G是AB的中点，BE＝6，求边AD的长．























20．(10分)如图，在▱ABCD中，∠DAB＝60°，点E、F分别在CD、AB的延长线上，且AE＝AD，CF＝CB.


(1)求证：四边形AFCE是平行四边形；


(2)若去掉已知条件“∠DAB＝∠60°”，(1)中的结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由．



































21．(9分)如图，在▱ABCD中，AE、AF是平行四边形的高，∠BAE＝30°，BE＝2，CF＝1，DE交AF于点G.


(1)求线段DF的长；


(2)求证：△AEG是等边三角形．

















22．(9分)如图，在▱ABCD中，AF平分∠BAD交BC于点F，CE平分∠BCD交AD于点E.


(1)若AD＝12，AB＝8，求CF的长；


(2)连结BE和AF相交于点G，DF和CE相交于点H，求证：EF和GH互相平分．

















23．(10分)如图，在▱ABCD中，对角线AC、BD相交于点O，AB⊥AC，AB＝3 cm，BC＝5 cm.点P从A点出发沿AD方向匀速运动，速度为1 cm/s.连结PO并延长交BC于点Q，设运动时间为t(0＜t＜5)．


(1)当t为何值时，四边形ABQP是平行四边形？


(2)设四边形OQCD的面积为y(cm2)，求y与t之间的函数关系式．


(3)是否存在某一时刻t，使点O在线段AP的垂直平分线上？若存在，求出t的值；若不存在，请说明理由．


(备用图)






































参考答案


一、


1．D


2．D


3．C


4．B


5. B


【解析】∵在▱ABCD中，CE平分∠BCD交AD于点E，∴∠DEC＝∠ECB，∠DCE＝∠BCE，AB＝DC，∴∠DEC＝∠DCE，∴DE＝DC＝AB.∵AD＝7，AE＝4，∴AB＝DE＝3.


A


【解析】∵四边形ABCD是平行四边形，


∴AB＝DC，AC＝2AO，BD＝2OD.


∵AO＝4，OD＝7，


∴BD＝14，AC＝8，


∴C△DBC－C△ABC＝BD＋BC＋DC－AC－BC－AB＝BD－AC＝14－8＝6.


7．A


【解析】∵四边形ABCD是平行四边形，AC＝10 cm，BD＝6 cm，


∴OA＝OC＝eq \f(1,2)AC＝5 cm，


OB＝OD＝eq \f(1,2)BD＝3 cm.


∵∠ODA＝90°，


∴AD＝eq \r(OA2－OD2)＝4 cm.


8．B


【解析】∵四边形ABCD是平行四边形，


∴AD∥BC，AD＝BC，∠BAD＝∠BCD，


∴当①AE∥CF时，四边形AECF是平行四边形，故正确；


当②BE＝FD时，CE＝AF，则四边形AECF是平行四边形，故正确；


当③∠1＝∠2时，∠EAF＝∠ECF.


∵∠EAF＋∠AEC＝180°，∠AFC＋∠ECF＝180°，


∴∠AFC＝∠AEC，


∴四边形AECF是平行四边形，故正确；


④若AE＝CF，则四边形AECF是平行四边形或等腰梯形，故错误．


D


【解析】∵M为CD的中点，


∴CM＝DM＝eq \f(1,2)CD＝eq \f(1,2)AB＝BC＝AD，


∴∠DAM＝∠DMA，∠CBM＝∠CMB.


∵∠C＋∠D＝180°，


∴∠C＝2∠DMA，∠D＝2∠CMB


∴∠DMA＋∠CMB＝eq \f(1,2)(∠C＋∠D)＝90°，


∴∠AMB＝180°－eq \f(1,2)(∠DMA＋∠CMB)＝90°，


即△MAB为直角三角形．


∵BM＝1，AM＝2，∴CD＝AB＝eq \r(5).


10．B


二、


11．14


【解析】在▱ABCD中，OC＝eq \f(1,2)AC，OB＝eq \f(1,2)BD，BC＝AD＝6，∴OC＋OB＝eq \f(1,2)(AC＋BD)＝8，∴△BOC的周长为14.


12．10


【解析】由平行四边形性质知，AD＝BC＝3，AB＝CD＝2，由平移性质知AD＝AE＝3，CD＝CE＝2，∴DE＝4.∴△ADE的周长为10.


13．4


【解析】∵四边形ABCD是平行四边形，


∴AB∥CD，AD∥BC，


AB＝CD＝6，BC＝AD＝8，


∴∠F＝∠ECD，∠DEC＝∠ECB.


∵CE平分∠BCD，∴∠ECD＝∠BCE，


∴∠F＝∠BCE＝∠ECD＝∠DEC＝∠AEF，


∴DE＝DC＝6，AE＝AF，


∴AE＝AD－DE＝2，∴AE＋AF＝4.


14．24


15．互相平分


16．①②④


【解析】∵四边形ABCD是平行四边形，


∴AB＝CD，BC＝AD＝8 cm，


AB∥DF，AD∥BC，


∴∠BEA＝∠EAD.


∵AE平分∠BAD，∴∠BAE＝∠EAD，


∴∠BEA＝∠BAE，∴AB＝BE＝4 cm，


∴CE＝BC－BE＝8 cm－4 cm＝4 cm，①正确；


∵AB∥DF，∴∠ABE＝∠FCE.


在△BAE和△CFE中，eq \b\lc\{(\a\vs4\al\c1(∠ABE＝∠FCE，,BE＝CE，,∠BEA＝∠CEF，))


∴△BAE≌△CFE(AAS)，


∴∠EFC＝∠BAE，AB＝CF，AE＝EF，


∴线段AF、BC互相平分，②正确；


∵AB＝CF，AB＝CD，∴CF＝CD＝4，


∴CE＝CF，只有∠B＝60°时，


∠F＝∠ADF＝60°，才能AC⊥DF，


而∠B没有给出60°的条件，


∴AC不一定垂直DF，③错误；


∵∠EFC＝∠BAE，∠BAE＝∠EAD，


∴∠EFC＝∠EAD.


∵AE＝EF，∴DE⊥AF，④正确．








三、


17．


证明：∵四边形ABCD为平行四边形，


∴AD∥BC，AD＝BC，


∴∠DAE＝∠AEB.


∵∠AEB＝∠B，


∴AB＝AE，


∴∠B＝∠DAE.


∵在△ABC和△EAD中，


eq \b\lc\{(\a\vs4\al\c1(AB＝AE，,∠B＝∠DAE，,BC＝AD，))


∴△ABC≌△EAD(SAS)，


∴AC＝DE.


18．


(1)证明：∵AB∥CD，


∴∠B＝∠D.


在△ABE和△CDF中，


eq \b\lc\{(\a\vs4\al\c1(∠B＝∠D，,AB＝CD，,∠BAE＝∠DCF，))


∴△ABE≌△CDF(ASA)，


∴AE＝CF.


(2)解：四边形AECF是平行四边形．


证明：由(1)△ABE≌△CDF得AE＝CF，∠AEB＝∠CFD，


∴180°－∠AEB＝180°－∠CFD，


即∠AEF＝∠CFE.


∴AE∥CF.


又∵AE＝CF，


∴四边形AECF是平行四边形．


19．


(1)证明：∵四边形ABCD是平行四边形，


∴AD∥BC.


∵AF＝CE，


∴四边形AFEC是平行四边形，


∴AC∥EF.


(2)解：∵AD∥BC，


∴∠F＝∠GEB.


∵点G是AB的中点，


∴AG＝BG.


在△AGF和△BGE中，


eq \b\lc\{(\a\vs4\al\c1(∠F＝∠GEB，,∠AGF＝∠BGE，,AG＝BG，))


∴△AGF≌△BGE(AAS)，


∴AF＝BE＝6.


∵AF＝CE＝6，


∴BC＝BE＋EC＝12.


∵四边形ABCD是平行四边形，


∴AD＝BC＝12.


20．


(1)证明：∵四边形ABCD是平行四边形，


∴DC∥AB，∠DCB＝∠DAB＝60°，


∴∠ADE＝∠CBF＝60°.


∵AE＝AD，CF＝CB，


∴△AED、△CFB为等边三角形，


∴∠AEC＝∠BFC＝60°，∠EAF＝∠FCE＝120°，


∴四边形AFCE是平行四边形．


(2)解：结论仍成立．


证明：∵四边形ABCD是平行四边形，


∴DC∥AB，∠CDA＝∠CBA，∠DCB＝∠DAB，AD＝BC，DC＝AB.


∴∠ADE＝∠CBF.


∵AE＝AD，CF＝CB，


∴∠AED＝∠ADE，∠CFB＝∠CBF.


∴∠AED＝∠CFB.


∵CE∥AF


∴∠AED＋∠EAF＝∠CFB＋∠FCE＝180°


∴∠EAF＝∠FCE.


∴四边形EAFC是平行四边形．


21．


(1)解：∵在平行四边形ABCD中AE、AF是高，


∴∠AEB＝∠AEC＝90°，∠AFD＝90°，AD∥BC，


∴∠DAE＝∠AEB＝90°，∠ADE＝∠DEC.


∵在Rt△ABE中∠BAE＝30°，BE＝2，


∴AB＝4，∠ABE＝60°.


∵四边形ABCD是平行四边形，


∴∠ABE＝∠ADC＝60°，CD＝AB＝4.


∵CF＝1，CD＝4，∴DF＝CD－CF＝4－1＝3.


(2)证明：∵在△ADF中∠ADC＝60°，


∠AFD＝90°，∴∠DAF＝30°，∴AD＝6.


∵四边形ABCD是平行四边形，∠ABE＝60°，


∴∠DAB＝∠C＝120°，BC＝AD＝6，


∴EC＝4，又∵CD＝4，


∴EC＝CD，[来源:学§科§网Z§X§X§K]


∴∠DEC＝∠EDC＝30°.


∵由(1)知∠AEC＝90°，∴∠AEG＝60°.


∵∠BAE＝30°，∠DAF＝30°，


∴∠EAG＝∠DAB－∠BAE－∠DAF＝60°，


∴∠AGE＝∠EAG＝∠AED＝60°，


∴△AEG是等边三角形．





22．


(1)解：∵四边形ABCD是平行四边形，


∴AD∥BC，BC＝AD＝12，∠BAD＝∠BCD，


∠ABF＝∠CDE，AB＝CD，∴∠DAF＝∠AFB.


∵AF平分∠BAD，∴∠BAF＝∠DAF，


∴∠AFB＝∠BAF，∴BF＝AB＝8，


∴CF＝BC－BF＝12－8＝4.


(2)证明：∵∠BAD＝∠BCD，


AF平分∠BAD，CE平分∠BCD，


∴∠BAF＝∠DAF＝∠FCE＝∠DCE，


∴∠DAF＝∠AFB，


∴∠FCE＝∠AFB，∴AF∥CE.


由(1)中可知AB＝BF，DE＝CD


又∵AB＝CD，


∴BF＝DE.


又∵DE∥BF，∴四边形BF是平行四边形，


∴DF∥BE.


又∵AF∥CE，∴四边形EGFH是平行四边形，


∴EF和GH互相平分．


23．


解：(1)∵四边形ABCD是平行四边形，


∴OA＝OC，AD∥BC，


∴∠PAO＝∠QCO.


又∵∠AOP＝∠COQ，


∴△APO≌△CQO(ASA)，


∴AP＝CQ＝t.


∵AB＝3，AC＝4，∠，BAC＝90°，


∴BC＝5，


∴BQ＝5－t.


∵AP∥BQ，


当AP＝BQ时，四边形ABQP是平行四边形，


即t＝5－t，∴t＝eq \f(5,2)，


∴当t＝eq \f(5,2)时，四边形ABQP是平行四边形．


(2)如答图1，过点A作AH⊥BC于点H，过点O作OG⊥BC于点G，连结OH.


在Rt△ABC中，∵AB＝3，BC＝5，∴AC＝4，


∴CO＝eq \f(1,2)AC＝2，


S△ABC＝eq \f(1,2)AB·AC＝eq \f(1,2)BC·AH，


∴3×4＝5AH，


∴AH＝eq \f(12,5).


∵AH∥OG，OA＝OC，


在Rt△AHC中，OH＝OC＝OA，


又∵OG⊥CH，


∴GH＝CG，


∴根据面积公式易得，OG＝eq \f(1,2)AH＝eq \f(6,5)，


∴y＝S△OCD＋S△OCQ＝eq \f(1,2)OC·CD＋eq \f(1,2)CQ·OG，


∴y＝eq \f(1,2)×2×3＋eq \f(1,2)×t×eq \f(6,5)＝eq \f(3,5)t＋3.


(答图1) (答图2)


(3)存在．


如答图2，∵OE是AP的垂直平分线，


∴AE＝eq \f(1,2)AP＝eq \f(t,2)，∠AEO＝90°，


由(2)知：AO＝2，OE＝eq \f(6,5)，


由勾股定理得：AE2＋OE2＝AO2，


∴(eq \f(1,2)t)2＋(eq \f(6,5))2＝22，


∴t＝eq \f(16,5)或－eq \f(16,5)(舍去)，


∴当t＝eq \f(16,5)时，点O在线段AP的垂直平分线上．











关闭Wrd文档返回原板块。