数学九年级下册7.1 正切一等奖备课ppt课件

这是一份数学九年级下册7.1 正切一等奖备课ppt课件，共22页。PPT课件主要包含了探究新知，尝试与交流，忆一忆，做一做，畅所欲言等内容，欢迎下载使用。

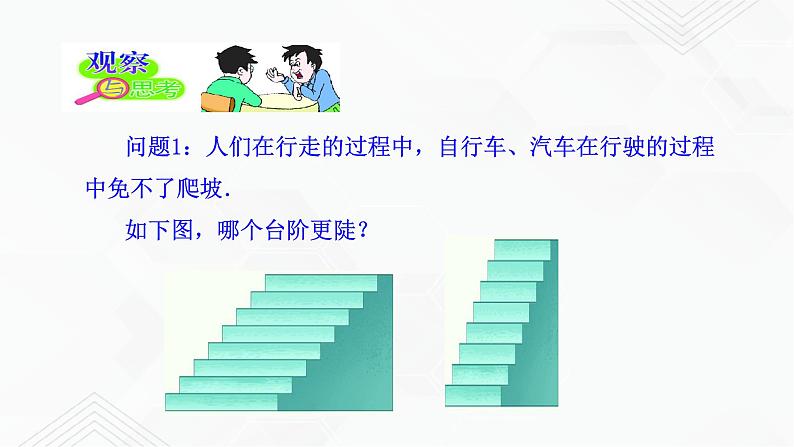
　问题1：人们在行走的过程中，自行车、汽车在行驶的过程中免不了爬坡．　如下图，哪个台阶更陡？
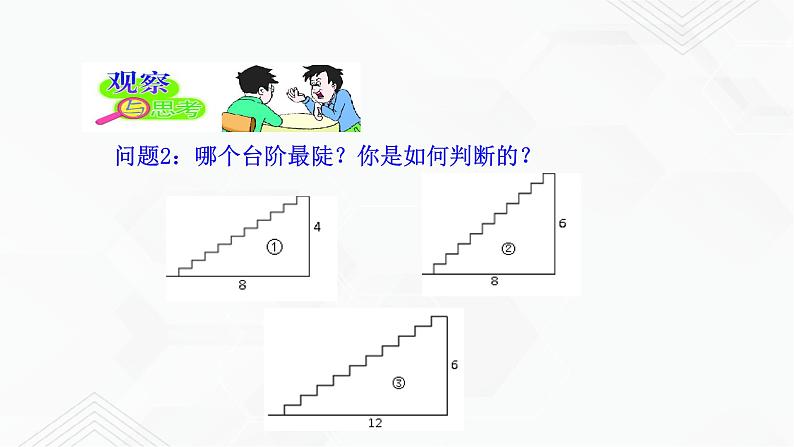
问题2：哪个台阶最陡？你是如何判断的？
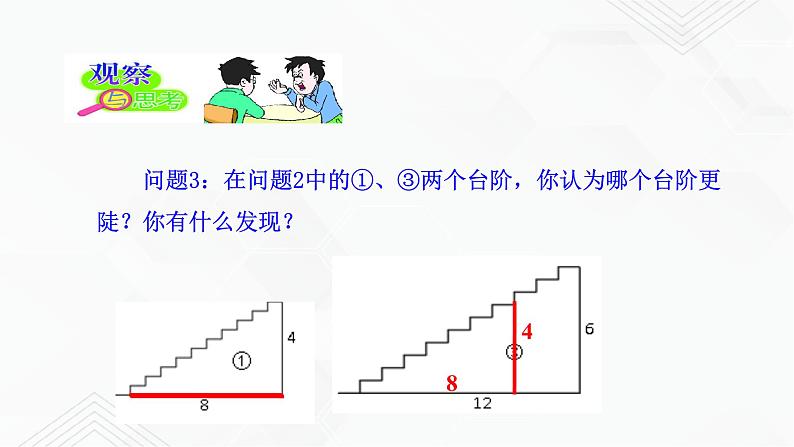
　　问题3：在问题2中的①、③两个台阶，你认为哪个台阶更陡？你有什么发现？
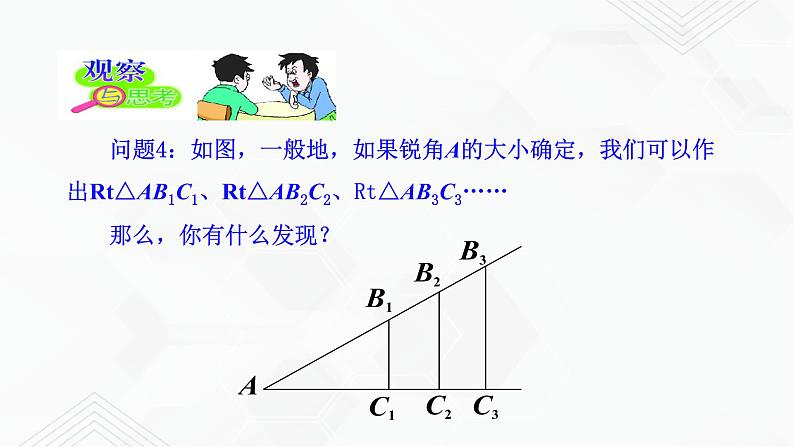
　问题4：如图，一般地，如果锐角A的大小确定，我们可以作出Rt△AB1C1、Rt△AB2C2、Rt△AB3C3……　那么，你有什么发现？
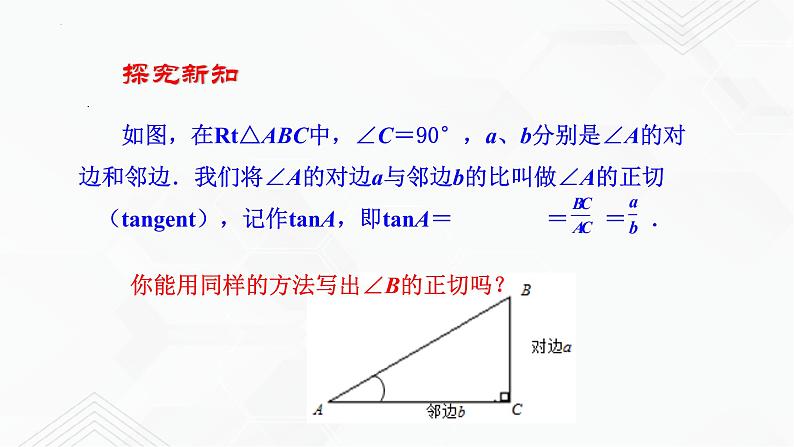
你能用同样的方法写出∠B的正切吗？
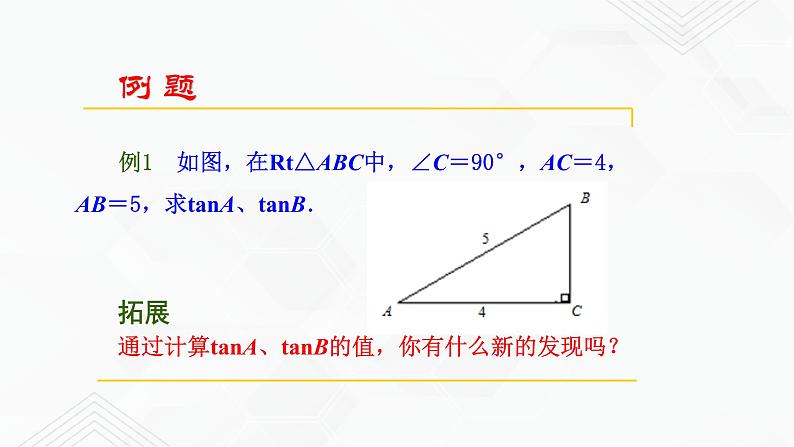
　例1　如图，在Rt△ABC中，∠C＝90°，AC＝4，AB＝5，求tanA、tanB．
通过计算tanA、tanB的值，你有什么新的发现吗？
例2　如图，在等边三角形ABC中，AB＝2，求tanA．
　　通过计算tanA的值，你对60º的正切值有什么认识？30º呢？你还能得到其他的吗？
1．如图，求下列图中各直角三角形中锐角的正切值．
2．如图，在Rt△ABC中，∠C＝90°， AB＝10， tanA ，求AC 、BC和tanB．
　　如图1，在Rt△ABC中，∠C＝90°，a、b分别是∠A的对边和邻边． 　　①∠A＝30°，a＝1，求tanA.　　②∠A＝45°，求tanA．　　③∠A＝60°，求tanA．
怎样计算任意一个锐角的正切值呢？
如图2，我们可以这样来确定tan65°的近似值：当一个点从点O出发沿着65°线移动到点P时，这个点沿水平方向前进了1个单位长度，沿垂直方向上升了约2.14个单位长度.于是，可知tan65°的近似值为2.14.
你能求其他角度的近似值吗？
请用同样的方法，写出下表中各角正切的近似值.
当锐角α越来越大时，α的正切值有什么变化？
你能求tan22°18′、 tan51.28°的值吗？试试看！
　用计算器求tan65°（精确到0.01）．
　　例1　如图3，当光线与水平线的夹角为32°时，测得学校旗杆的影长为28m，求旗杆的高度(精确到0.01m)．
　例2　如图4，这是一个梯形大坝的横断面，根据图中的尺寸，请你通过计算判断左右两个坡的倾斜程度哪一个更大一些？
　例3 如图5，在Rt△ABC中，∠CAB＝90°，AD是∠CAB的平分线，tanB＝ ，则 ＝______.
　 如图6，在Rt△ABC中，∠ACB＝90°，CD是AB边上的高，AC＝3，AB ＝ 5，求∠ACD 、∠BCD的正切值．
通过这节课的学习，我的收获是…