

中考数学复习专题几何教学重难点专题:平面展开—最短路径问题含答案
展开1.如图所示,一圆柱高AB为5cm,BC是底面直径,设底面半径长度为acm,求点P从A点出发沿圆柱表面移动到点C的最短路线.
方案设计
某班数学兴趣小组设计了两种方案:
图1是方案一的示意图,该方案中的移动路线的长度为l1,则l1=5+2a(cm);
图2是方案二的示意图,设l2是把圆柱沿AB侧面展开的线段AC的长度,则l2= cm(保留π).
计算探究
①当a=3时,比较大小:l1 l2(填“>”“=”或“<”);
②当a=4时,比较大小:l1 l2(填“>”“=”或“<”);
延伸拓展
在一般情况下,设圆柱的底面半径为rcm.高为hcm.
①若l12=l22,求h与r之间的关系;
②假定r取定值,那么h取何值时,l1<l2?
③假定r取定值,那么h取何值时,l1>l2?
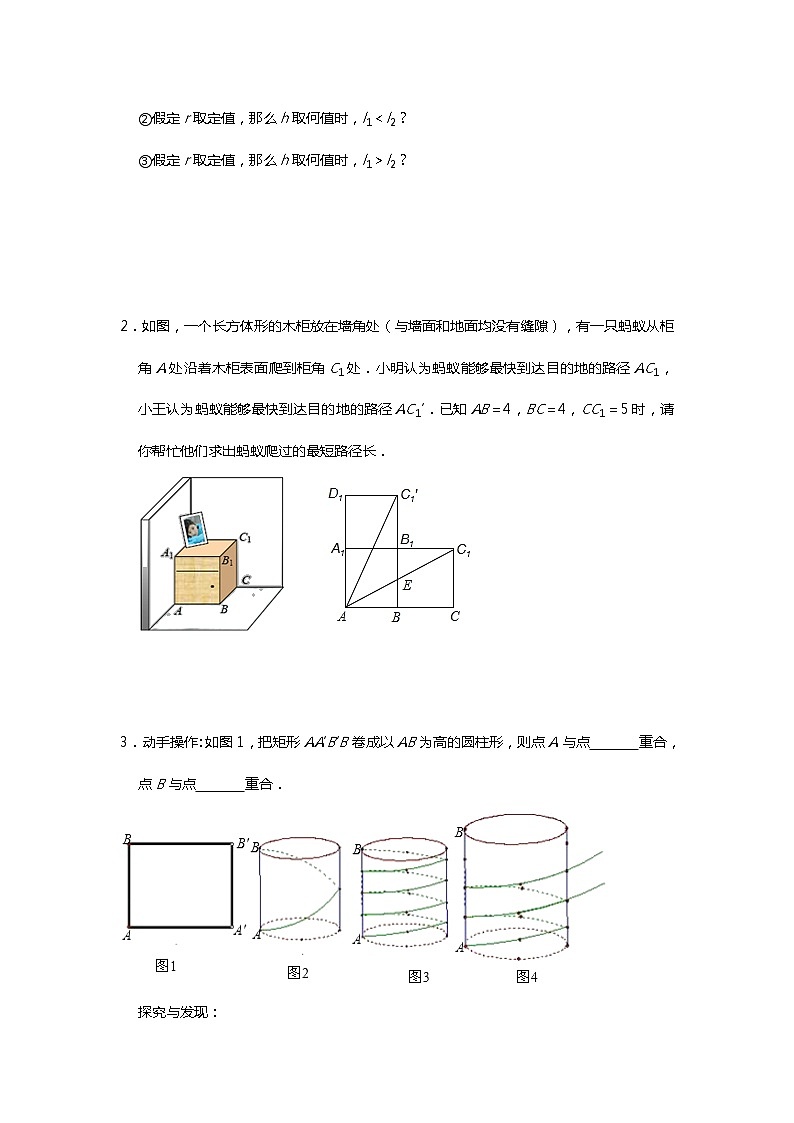
2.如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.小明认为蚂蚁能够最快到达目的地的路径AC1,小王认为蚂蚁能够最快到达目的地的路径AC1′.已知AB=4,BC=4,CC1=5时,请你帮忙他们求出蚂蚁爬过的最短路径长.
3.动手操作:如图1,把矩形AA′B′B卷成以AB为高的圆柱形,则点A与点 重合,点B与点 重合.
探究与发现:
(1)如图2,若圆柱的底面周长是30cm,高是40cm,从圆柱底部A处沿侧面缠绕一圈丝带到顶部B处作装饰,则这条丝线的最小长度是 cm;(丝线的粗细忽略不计)
(2)如图3,若用丝线从该圆柱的底部A缠绕4圈直到顶部B处,则至少需要多少丝线?
实践与应用:
如图4,现有一个圆柱形的玻璃杯,准备在杯子的外面缠绕一层装饰带,为使带子全部包住杯子且不重叠,需要将带子的两端沿AE,CF方向进行裁剪,如图5所示,若带子的宽度为1.5厘米,杯子的半径为6厘米,则sinα= .
4.李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.
(1)如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2)如图2,圆锥的母线长为4cm,底面半径r=cm,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.
(3)如图3,是一个没有上盖的圆柱形食品盒,一只蚂蚁在盒外表面的A处,它想吃到盒内表面对侧中点B处的食物,已知盒高10cm,底面圆周长为32cm,A距下底面3cm.
5.如果(1)所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图(2)所示已知展开图中每个正方形的边长为1.
(1)求在该展开图中可画出的最长线段的长度?这样的线段可以画几条?
(2)求∠B′A′C′的度数?说明理由.
(3)在图1中若蚂蚁从点A′沿着正方体的表面爬行到点C,试求爬行的最短路程.
6.如图①,一只蚂蚁从圆锥底面的A点出发,沿侧面绕行一周后到达母线SA的中点M.蚂蚁沿怎样的路径行走最合算?为了解决这一问题,爱动脑筋的银银、慧慧与乐乐展开了研究.
(1)善于表现的银银首先列出了一组数据:圆锥底面半径r=10cm,母线SA长为40cm,就这组数据,请你求出蚂蚁所走的最短路程;
(2)一向稳重的慧慧只给出一个数据:圆锥的锥角等于60°(如图②),请问:蚂蚁如何行走最合算?
(3)通过(1)、(2)的计算与归纳,银银、慧慧自认为他们已找到问题的解决方法,可老谋深算的乐乐认为他们考虑欠周,
①请你分析,乐乐为什么认为他们考虑欠周?
②结合上面的研究,请你给出这一问题的一般性解法.
7.某同学的茶杯是圆柱形,如图是茶杯的立体图,左边下方有一只蚂蚁,从A处爬行到对面的中点B处,如果蚂蚁爬行路线最短,请画出这条最短路线图.
解:如图1,将圆柱的侧面展开成一个长方形,如图示,则A、B分别位于如图所示的位置,连接AB,即是这条最短路线图.
问题:某正方体盒子,如图左边下方A处有一只蚂蚁,从A处爬行到侧棱GF上的中点M点处,如果蚂蚁爬行路线最短,请画出这条最短路线图.
8.如图1所示的纸杯,经测量(接缝处忽略不计),纸杯的杯口直径为7cm,底面直径为cm,母线长为8cm,该纸杯的侧面展开如图2所示,
(1)求纸杯的侧面展开图2中杯口所在圆的半径OA的长;
(2)若一只小虫从纸杯底面的点C出发,沿纸杯侧面爬行一周(如图3)回到点A.求小虫爬行的最短路程.(精确到1cm)
(3)请你设计一种方案,在一张矩形纸片上能够剪出该纸杯的侧面,并求出你所设计的矩形的面积,要求:尽可能小.(精确到1cm)
9.如图①,一个无盖的正方体盒子的棱长为10厘米,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙.(盒壁的厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,在图①画出一条路径,使昆虫乙从顶点A沿这条路径爬行,可以在最短的时间内捕捉到昆虫甲.(请简要说明画法)
(2)如图②,假设昆虫甲静止不动,昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
(3)如图②,假设昆虫甲从顶点C1,以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?(精确到1s).参考数据:≈4.4,≈4.6.
10.勾股定理是解决直角三角形很重要的数学定理.这个定理的证明的方法很多,也能解决许多数学问题.请按要求作答:
(1)用语言叙述勾股定理;
(2)选择图1、图2、图3中一个图形来验证勾股定理;
(3)利用勾股定理来解决下列问题:
如图4,一个长方体的长为8,宽为3,高为5.在长方体的底面上一点A处有一只蚂蚁,它想吃长方体上与A点相对的B点处的食物,则蚂蚁需要沿长方体表面爬行的最短路程是多少?
参考答案
1.解:l2=cm;
当a=3时,(l1)2=121;(l2)2=25+9π2;∴l1>l2,
当a=4时,(l1)2=169;(l2)2=25+16π2;
∴l1<l2,
故答案为;>;<.
①(2r+h)2=h2+π2r2,
r=;
②l12<l22时,l1<l2,
(2r+h)2<h2+π2r2,
h<,
③由②可得h>时,l1>l2.
2.解:蚂蚁沿着木柜表面经线段A1B1到C1,爬过的路径的长是
L1==;
蚂蚁沿着木柜表面经线段BB1到C1,爬过的路径的长是
L2==.
因为:L1>L2,
所以最短路径的长是L2=.
3.解:A′,B′;
探究与发现:
(1)如图,连接AB′,已知AA′=30,A′B′=40,由勾股定理,
得AB′==50;
(2)如图,在Rt△AA′C中,AA′=30,A′C==10,
∴AC===,
∴丝线至少为4×AC=cm;
实践与应用:如图,沿MN把矩形剪开,矩形对角线AA′为杯子周长12π,带子的宽度A′M=1.5厘米,
由互余关系可知∠A′MN=∠MAA′=α,
∴在Rt△AA′M中,sinα===.
4.解:(1)
(2)解:由已知条件:圆锥的母线长为4cm,底面半径r=cm,
∴2×,
∴可求出圆锥侧面展开图中圆心角:n=∠AOA1=120°,
∴∠AOC=60°,sin60°==,
∴进一步可求得最短的路程为AA1=.
(3)如图,作出点A关于CD的对称点A'.
根据题意求出BF=CD=,
可构造直角三角形或利用相似三角形等有关知识
求出BA'=20cm,
所以蚂蚁吃到食物的爬行的最短路程为AE+BE=BA'=20cm
5.解:(1)如图2,AH=1+1+1=3,CH=1,
即最长线段AC的长度是:=,这样的线段可以画4条,如图(2)线段EB′、线段FM、线段A′C′、线段GH;且线段的长度都是;
(2)连接A′C′,
由图形可知:∠A′B′E=∠C′B′E=45°,A′B′=B′C′=,
∴∠A′B′C′=90°,
即△A′B′C′是等腰直角三角形,
∴∠B′A′C′=45°;
(3)如图所示展开:连接A′C,则线段A′C的长就是蚂蚁从点A′沿着正方体的表面爬行到点C的最短路程,
在Rt△A′C′C中,A′C′=1+1=2,C′C=1,∠A′C′C=90°,
由勾股定理得:A′C==.
6.解:(1)2π•10=nπ•40÷180°
n=90°,
AM==20.
(2)∵锥角为60°,
∴底面直径的长和母线的长相等,
但缺少母线的长.
(3)①因为根据银银的数据得到的圆心角是90°,不具有一般性,因为慧慧缺少条件.
②(1)展成平面图形.
(2)知道母线的长,知道扇形的圆心角度数,以及M是SA的中点,根据三角函数或者构造直角三角形来求解.
7.解:如图所示:AM为最短路线.
8.解:(1)设∠O的度数是n,
则7π=,=,
解得:OA=42,n=30°;
(2)在图2中,沿CA剪开,得出扇形AOA′,连接CA′,则CA′的长度是小虫爬行的最短路程,
过C作CE⊥OA′于E,
在Rt△COE中,OC=34,∠O=30°,
∴CE=17,OE=17,
∴A′E=42﹣17,
在Rt△CEA′中,CA′=≈21cm,
(3)此方案设计的矩形的长约为21cm,宽约为10cm,面积为21×10=210(cm2)
9.解:(1)画出图①中A⇒E2⇒C1,A⇒E3⇒C1,A⇒E4⇒C1中任意一条路径;(E1、E2、E3分别为各棱中点)
(2)如图2,根据昆虫甲静止不动,昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,
AC1==10cm,
故昆虫乙至少需要爬行:10÷2=5秒,
答:昆虫乙至少需要5时间才能捕捉到昆虫甲;
(3)由(1)可知,当昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙可以沿下列四种路径中的任意一种爬行:
可以看出,图②﹣1与图②﹣2中的路径相等,图②﹣3与图②﹣4中的路径相等.
①设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F爬行捕捉到昆虫甲需x秒钟,
如图②﹣1﹣1,在Rt△ACF中,
(2x)2=(10﹣x)2+202,
解得x=10秒;
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E2→F爬行捕捉到昆虫甲需y秒钟,
如图②﹣1﹣2,在Rt△ABF中,
(2y)2=(20﹣y)2+102,
解得y≈8秒;
所以昆虫乙从顶点A爬行捕捉到昆虫甲至少需8秒钟.
10.解:(1)在直角三角形中,两条直角边的平方和等于斜边的平方.
(2)(2)∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°.
∵S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED,
∴(a+b)(a+b)=ab+ab+c2.
整理,得a2+b2=c2.
(3)把长方体表面展开,转化为平面图形,当长、宽、高互不相等时,要分三种情况,根据勾股定理分别求出.
①当展开图形为:②当展开图为:③当展开图为:
①AB=②AB=
③AB=
∵128<146<172
∴蚂蚁需要沿长方体表面爬行的最短路程是8.
专题53 巧用图形的平移解决几何问题-中考数学重难点专项突破(全国通用): 这是一份专题53 巧用图形的平移解决几何问题-中考数学重难点专项突破(全国通用),文件包含专题53巧用图形的平移解决几何问题原卷版docx、专题53巧用图形的平移解决几何问题解析版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
专题51 巧用图形的翻折解决几何问题-中考数学重难点专项突破(全国通用): 这是一份专题51 巧用图形的翻折解决几何问题-中考数学重难点专项突破(全国通用),文件包含专题51巧用图形的翻折解决几何问题原卷版docx、专题51巧用图形的翻折解决几何问题解析版docx等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。
专题52 巧用图形的旋转解决几何问题-中考数学重难点专项突破(全国通用): 这是一份专题52 巧用图形的旋转解决几何问题-中考数学重难点专项突破(全国通用),文件包含专题52巧用图形的旋转解决几何问题原卷版docx、专题52巧用图形的旋转解决几何问题解析版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。












